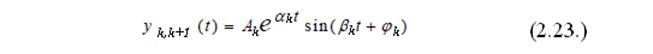Что значит устойчивая система

Что значит устойчивая система

В этом разделе рассматриваются важнейшие характеристики качества управляемых систем. Этими характеристиками являются устойчивость систем, точность и помехоустойчивость.

Понятие устойчивости относится к ситуации, когда входные сигналы системы равны нулю, т.е. внешние воздействия отсутствуют. При этом правильно построенная система должна находиться в состоянии равновесия (покоя) или постепенно приближаться к этому состоянию. В неустойчивых системах даже при нулевых входных сигналах возникают собственные колебания и, как следствие, – недопустимо большие ошибки.

Понятие точности связано с качеством работы управляемых систем при изменяющихся входных сигналах. В правильно спроектированных системах управления величина рассогласования между заданным законом управления g(t) и выходным сигналом x(t) должна быть мала.

Наконец, для характеристики влияния помех на системы управления используют дисперсию или среднее квадратическое отклонение составляющей ошибки за счет действия помех.

Одним из первых вопросов, возникающих при исследовании и проектировании линейных систем управления, является вопрос об их устойчивости. Линейная система называется устойчивой, если при выведении ее внешними воздействиями из состояния равновесия (покоя) она возвращается в него после прекращения внешних воздействий. Если после прекращения внешнего воздействия система не возвращается к состоянию равновесия, то она является неустойчивой. Для нормального функционирования системы управления необходимо, чтобы она была устойчивой, так как в противном случае в ней возникают большие ошибки.

Определение устойчивости обычно проводят на начальном этапе создания системы управления. Это объясняется двумя причинами. Во-первых, анализ устойчивости довольно прост. Во-вторых, неустойчивые системы могут быть скорректированы, т.е. преобразованы в устойчивые с помощью добавления специальных корректирующих звеньев.

Анализ устойчивости с помощью алгебраических критериев

Устойчивость системы связана с характером ее собственных колебаний. Чтобы пояснить это, предположим, что система описывается дифференциальным уравнением

или, после преобразования Лапласа,

,

где g(p) – входное воздействие.

В каких же случаях система устойчива?

Предположим, что pk = ak – действительный корень.

Допустим теперь, что – комплексный корень характеристического уравнения. Заметим, что в этом случае также будет корнем характеристического уравнения. Двум комплексно-сопряженным корням будут соответствовать слагаемые вида , .

Таким образом, система устойчива, если действительные части всех корней характеристического уравнения отрицательны. Если хотя бы один корень имеет действительную часть ak ³ 0, то система неустойчива. Говорят, что система находится на границе устойчивости, если хотя бы один корень характеристического уравнения имеет нулевую действительную часть, а действительные части всех остальных корней отрицательны.

Это определение хорошо иллюстрируется геометрически. Представим корни характеристического уравнения точками на комплексной плоскости (рис. 15).

Рассмотрим в качестве примера замкнутую систему управления c одним интегрирующим звеном. В этом случае H(p) = , , а передаточная функция замкнутой системы

.

© 2021 Научная библиотека

Копирование информации со страницы разрешается только с указанием ссылки на данный сайт

Источник

Устойчивость систем автоматического управления

ЛЕКЦИЯ 7.

На предыдущих лекциях исследовались установившиеся процессы в САУ. Сейчас мы переходим к рассмотрению переходных процессов. Начнем их рассматривать с понятия устойчивости.

Любая система должна быть прежде всего работоспособной. Это значит, что она должна нормально функционировать при действии на нее различных внешних возмущений. Иными словами, система должна работать устойчиво.

Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.

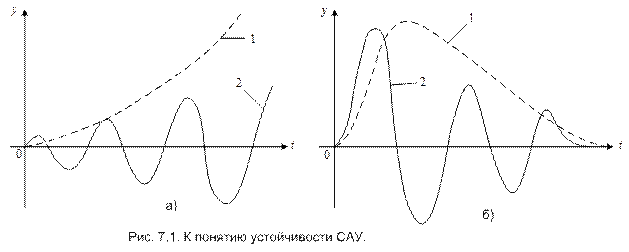
На рис. 7.1 показаны типичные кривые переходных процессов в неустойчивой (рис. 7.1, а) и устойчивой (рис. 7.1, б) системах. Если система неустойчива, то достаточно любого толчка, чтобы в ней начался расходящийся процесс ухода из исходного установившегося состояния. Этот процесс может быть апериодическим (кривая 1 на рис. 7.1, а) или колебательным (кривая 2 на рис. 7.1, а).

Апериодический расходящийся процесс может, например, возникнуть в САУ, если в ее управляющем устройстве ошибочно переключить полярность воздействия на объект, в результате чего УУ будет осуществлять не отрицательную, а положительную обратную связь вокруг объекта. При этом УУ будет не устранять отклонение у, а действовать в обратном направлении, вызывая лавинообразное его изменение.

Колебательный расходящийся процесс может наступить, например, при неограниченном увеличении коэффициента передачи системы. Вследствие чего УУ станет излишне энергично воздействовать на объект, стремясь ликвидировать первоначально возникшие отклонения у. В этом случае при каждом очередном возврате у к нулю под действием управляющего устройства кривая у будет пересекать ось абсцисс все с большей скоростью и процесс в целом будет расходящимся.

В случае устойчивой системы (рис. 7.1, б) переходный процесс, вызванный каким-либо воздействием, со временем затухает апериодически (кривая 1) или колебательно (кривая 2), и система вновь возвращается в установившееся состояние.

Таким образом, устойчивую систему можно определить также как систему, переходные процессы в которой являются затухающими.

Приведенное понятие устойчивости определяет устойчивость установившегося режима системы. Однако система может работать в условиях непрерывно изменяющихся воздействий, когда установившийся режим вообще отсутствует. С учетом таких условий работы можно дать следующее, более общее определение устойчивости: система устойчива, если ее выходная величина остается ограниченной в условиях воздействия на систему ограниченных по величине возмущений.

Нетрудно показать, что если переходный процесс в системе является затухающим, то система будет удовлетворять и последнему определению.

Линейная система автоматического управления называется устойчивой, если ее выходная координата у(t) остается ограниченной при любых ограниченных по абсолютной величине входных воздействиях х(t) и f(t). Устойчивость линейной системы определяется ее характеристиками и не зависит от действующих воздействий.

. (7.1)

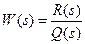
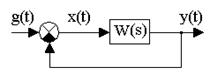
Рис. 7.2. Структурная схема линейной системы

Передаточная функция замкнутой системы, изображенной на рис. 7.2, определяется по следующей формуле

. (7.2)

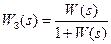
Подставив (7.1) в (7.2) и освободившись от дробей в числителе и знаменателе передаточной функции замкнутой системы, можно представить ее так:

, (7.3)

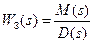
где ; ; .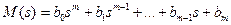

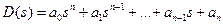
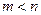
Процессы в системе (рис.7.2), как следует из (7.3), описываются дифференциальным уравнением вида

. (7.4)

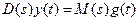
Решение линейного неоднородного уравнения (7.4) в общем виде состоит, как известно, из двух составляющих:

. (7.5)

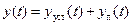
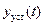
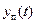
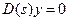
Здесь — частное решение неоднородного уравнения (7.5) с правой частью, описывающее вынужденный режим системы, устанавливающийся по окончании переходного процесса; — общее решение однородного уравнения

,

описывающее переходный процесс в системе.

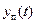
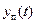
Как показано выше, система будет устойчива, если переходные процессы , вызванные любыми возмущениями, будут затухать, т.е. если с течением времени будет стремиться к нулю.

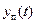
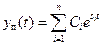
Решение однородного дифференциального уравнения, как известно, имеет вид:

. (7.6)

Здесь С_i – постоянные интегрирования, определяющиеся начальными условиями и возмущением; s_i – корни характеристического уравнения

, (7.7)

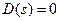
где полином 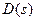, называемый характеристическим, есть левая часть уравнения (7.4) динамики системы.

Из теории комплексных переменных известно, что если вещественная часть корня s_i отрицательна, то слагаемое 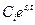стремится к нулю при t ® ¥.

Таким образом, для устойчивости системы необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части.

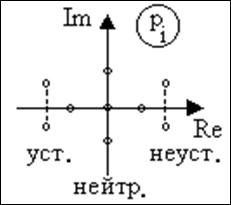
Если изобразить корни характеристического уравнения системы точками на комплексной плоскости (рис. 7.3), то найденное выше общее условие устойчивости линейной системы можно сформулировать еще так: условием устойчивости системы является расположение всех корней характеристического уравнения, т.е. полюсов передаточной функции системы, в левой комплексной полуплоскости или, короче, все они должны быть левыми.

Рис. 7.3. Корни характеристического уравнения на комплексной плоскости.

Наличие корня на мнимой оси означает, что система находится на границе устойчивости. При этом возможны два случая:

— корень в начале координат;

— пара мнимых корней.

Нулевой корень появляется, когда свободный член характеристического уравнения равен нулю. В этом случае границу устойчивости называют апериодической; система устойчива не относительно выходного сигнала, а относительно его производной: выходной сигнал в установившемся режиме имеет произвольное значение. Такие системы называют нейтрально устойчивыми.

В том случае, когда характеристическое уравнение имеет пару мнимых корней, границу устойчивости называют колебательной, при этом в переходном процессе будут незатухающие гармонические колебания.

Если хотя бы один из корней имеет положительную вещественную часть, т.е. лежит в правой полуплоскости комплексной плоскости корней характеристического уравнения, то система неустойчивая.

Для суждения об устойчивости системы практически не требуется находить корней ее характеристического уравнения в связи с тем, что разработаны косвенные признаки, по которым можно судить о знаках действительных частей этих корней и тем самым об устойчивости системы, не решая самого характеристического уравнения. Эти косвенные признаки называются критериями устойчивости.

Существуют три основных критерия устойчивости: критерий Рауса-Гурвица, критерий Михайлова и критерий Найквиста. Рассмотрим их последовательно.

Источник

Определение устойчивости систем автоматического управления промышленными роботами

Введение

Необходимым условием работоспособности системы автоматического управления (САУ), является её устойчивость. Под устойчивостью принято понимать свойство системы восстанавливать состояние равновесия, из которого она была выведена под влиянием возмущающих факторов после прекращения их воздействия [1].

Постановка задачи

Теория просто и кратко

Анализ устойчивости системы по методу Михайлова сводится к построению характеристического многочлена замкнутой системы (знаменатель передаточной функции), комплексной частотной функции (характеристического вектора):

(1)

где и – соответственно вещественная и мнимая части знаменателя передаточной функции, по виду которой можно судить об устойчивости системы.

Замкнутая САУ устойчива, если комплексная частотная функция , начинаясь на
стрелки начало координат, проходя последовательно n квадрантов, где n – порядок характеристического уравнения системы, т. е.

(2)

Рисунок 1. Амплитудно-фазовые характеристики (годографы) критерия Михайлова: а) – устойчивой системы; б) – неустойчивой системы (1, 2) и системы на границе устойчивости (3)

САУ электроприводом манипулятора промышленного робота (МПР)

Рисунок 2 – Структурная схема САУ электроприводом МПР

Передаточная функция данной САУ имеет следующее выражение [2]:

(3)
где kу – коэффициент усиления усилителя, kм – коэффициент пропорциональности частоты вращения двигателя величине напряжения на якоре, Tу – электромагнитная постоянная времени усилителя, Tм – электромеханическая постоянная времени двигателя с учётом инерции нагрузки (по своим динамическим характеристикам двигатель представляет собой передаточную функцию последовательно соединённых инерционного и интегрирующего звеньев), kдс – коэффициент пропорциональности между входной и выходной величинами датчика скорости, K – коэффициент усиления главной цепи: .

Численные значения в выражение передаточной функции следующие:

K = 100 град / (В∙с); kдс = 0,01 В / (град∙с); Tу = 0,01 с; Tм = 0,1с.

Далее запишем характеристический многочлен замкнутой системы

заменив s на :
(4)

Решение на Python

Здесь следует отметить, что подобные задачи на Python ещё никто не решал, во всяком случае я не нашёл. Это было связано с ограниченными возможностями работы с комплексными числами. С появлением SymPy можно сделать следующее:

Характеристический многочлен замкнутой системы –
-I*T1*T2*w**3 — T1*w**2 — T2*w**2 + I*w + 1

Сразу видим, что многочлен третьей степени. Теперь получим мнимую и действительную части в символьном отображении:

Сразу видим вторую степень действительной части и третью мнимой. Подготовим данные для построения годографа Михайлова. Введём численные значения для T1 и T2, и будем менять частоту от 0 до 100 с шагом 0.1 и построим график:

Из графика не видно, то годограф начинается на действительной положительной оси. Нужно изменить масштабы осей. Приведу полный листинг программы:

Теперь уже видно, что годограф начинается на действительной положительной оси. САУ устойчива, n=3, годограф совпадает с приведённым на первом рисунке.

Дополнительно убедится в том, что годограф начинается на действительной оси можно дополнив программу следующим кодом для w=0:

Начальная точка М(1,0)

САУ сварочного робота

Рисунок 3. Структурная схема САУ позиционированием НСУ

Характеристическое уравнение данной САУ будет иметь вид [1]:

где K – варьируемый коэффициент усиления системы, a – определённая положительная константа. Численные значения: K = 40; a = 0,525.

Далее путём замены s на , получим функцию Михайлова:
(5)

Решение на Python

Построенный годограф Михайлова, начинаясь на вещественной положительной оси (М (21,0)), огибает в положительном направлении начало координат, проходя последовательно четыре квадранта, что соответствует порядку характеристического уравнения. Значит, данная САУ позиционированием НСУ – устойчива.

Выводы

При помощи модуля SymPy Python получен простой и наглядный инструмент для решения задач расчёта устойчивости систем автоматического управления, что является обязательным условием работоспособности любого промышленного робота и манипулятора.

Источник

Устойчивость САУ, общие понятия устойчивости

Устойчивость системы автоматического управления — это свойство системы воз-

вращаться в исходное состояние равновесия после прекращения воздействия, выведшего систему состояния первоначального равновесия.

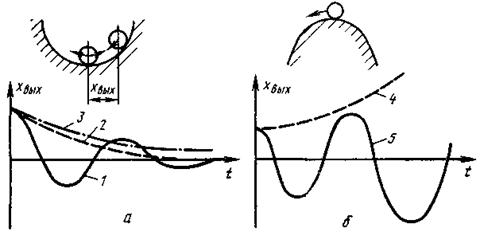
Примером устойчивых и неустойчивых систем могут служить системы из шарика, расположенного на вогнутой и выпуклой поверхности, представленные на рисунке 60.

Рис.60. Примеры систем: а) устойчивой; б) неустойчивой

На рисунке 60а шарик, расположенный на вогнутой поверхности и смещенный в сторону определенным усилием, после окончания внешнего воздействия возвратится в положение первоначального равновесия. При отсутствии трения о поверхность или его минимальном значении шарик будет совершать непродолжительные колебания около положения равновесия до возвращения в первоначальное положение равновесия (кривая 1— затухающий колебательный процесс). При большом трении шарик возвратится в положение первоначального равновесия без колебаний (кривая 2 — апериодический процесс). При очень большом значении трения шарик может не вернуться в положение первоначального равновесия (кривая 3), но возвратится в область, близкую к положению равновесия. В рассмотренном случае налицо наличие устойчивой системы. В устойчивых САУ возникают подобные переходные процессы (затухающие колебательные и апериодические).

На рисунке 60б шарик, расположенный на выпуклой поверхности и смещенный в сторону определенным усилием, не возвратится в положение первоначального равновесия (кривая 4), поэтому система является неустойчивой. В неустойчивых системах возникают переходные процессы виде расходящихся колебаний (кривая 5) или апериодические (кривая 4).

Неустойчивость САУ, как правило, возникает из-за очень сильного действия обратной связи. Причинами динамической неустойчивости обычно являются значительные инерционные характеристики звеньев замкнутой системы, из-за которых сигнал обратной связи в режиме колебаний так отстает от входного сигнала, что оказывается с ним в фазе. Получается, что характер действия отрицательной обратной связи приобретает характер

Составим математическое описание устойчивости и неустойчивости. Так как устойчивость системы зависит только от характера ее свободного движения, то данное свободное движение системы можно описать однородным дифференциальным уравнением:

(2.19.)

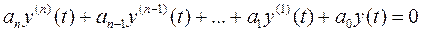
характеристическое уравнение, которого будет представлено следующим выражением:

(2.20.)

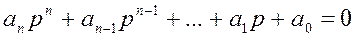
Общее решение однородного дифференциального уравнения (2.19.) представим в следующем виде:

(2.21.)

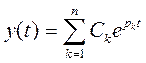
где C_k – постоянные, зависящие от начальных условий, p_k – корни характеристического уравнения.

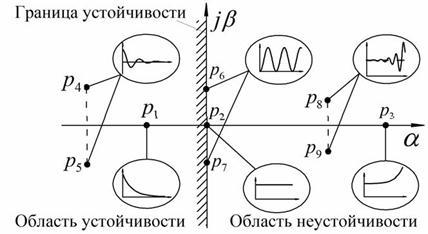
Корни характеристического уравнения могут быть комплексными (p_k = α_k ± jβ_k), действительными (p_k = α_k) или мнимыми (p_k= jβ_k). Комплексные корни всегда попарно сопряжены между собой, т.е. если имеется корень уравнения с положительной мнимой частью, то обязательно будет существовать корень с такой же по модулю, но отрицательной мнимой частью. y(t) при t→ ∞ из (2.21.) будет стремиться к нулю лишь тогда, когда каждое слагаемое С_к е p k t → 0. Характер данной функции будет зависеть от вида корня. Возможные случаи расположения корней p_kна комплексной плоскости и соответствующие им функции y(t) = С_ке p k t представлены на рисунке 61. Вид функций показан внутри эллипсов.

Рис.61. Влияние расположения корней характеристического уравнения на

составляющие свободного движения системы

На рисунке 61 видно, что если каждому действительному корню p_k = α_k для выражения (2.21.) будет соответствовать слагаемое:

тогда приα_к 0 (корень p₃ ) функция будет неограниченно возрастать, а при α_к = 0 (корень p₂ )функция будет оставаться постоянной.

Если характеристическое уравнение будет иметь комплексные корни, то каждой паре сопряженных комплексных корней p _{k, k+1}= α _k± jβ_{k ,} будут соответствовать два слагаемых, которые можно объединить и представить в виде следующего выражения:

Данная функция представляет собой синусоиду с изменяющейся по экспоненте амплитудой и частотой β_k. При отрицательной действительной части двух комплексных корней α_{к, к+1} 0, (корни p₈ и p₉) амплитуда колебаний будет увеличиваться неограниченно. При отсутствии действительной части комплексных корней α_{к, к+1} = 0 (корни p₆ и p₇), т.е. наличии только мнимых корней, функция будет представлять собой незатухающую синусоиду с частотой β_k.

Исходя из определения устойчивости, если первоначальное положение равновесия принимается за ноль, то у устойчивых систем величина выходного параметра с течением времени должна стремиться к нулю, т.е. система сама возвратится в положение равновесия. Необходимым и достаточным условием этого является, чтобы все слагаемые решения дифференциального уравнения (2.21.) с течением времени стремились к нулю, что может быть достигнуто при отрицательных действительных корнях уравнения, а комплексные корни должны иметь отрицательную действительную часть. Существование хотя бы одного положительного действительного корня или пары комплексных корней с положительной действительной частью приведет к тому, что величина выходного параметра системы не возвратится к первоначальному значению, т.е. система будет неустойчивой.

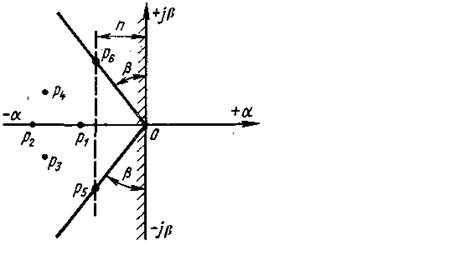
Анализируя местоположение корней характеристического уравнения на комплексной плоскости, представленное на рисунке 62, можно заметить, что САУ является устойчивой, если все корни характеристического уравнения находятся в левой полуплоскости и все они являются действительными отрицательными или комплексными с отрицательной действительной частью. Наличие хотя бы одного корня в правой полуплоскости будет характеризовать неустойчивость системы.

Устойчивость системы является внутренним свойством системы, зависящим только от вида корней характеристического уравнения, описывающего свойства системы, и не зависящим от внешнего воздействия. Необходимым и достаточным условием устойчивости системы является положение всех корней уравнения в левой (отрицательной) полуплоскости.

Точка β = 0 на мнимой оси соответствует нулевому корню. Считается, что уравнение, имеющее один нулевой корень, находится на апериодической границе устойчивости, а при наличии двух нулевых корней система неустойчива.

Рис.62. Расположение корней характеристического уравнения устойчивой системы на

Не стоит забывать, что уравнения почти всех реальных САУ не являются линейными, а приведены к линейным уравнениям с помощью линеаризации, поэтому допущения, сделанные при линеаризации, могут повлиять на правильность определения устойчивости системы.

А. М. Ляпунов в 1892 г. в своей работе «Общая задача об устойчивости движения» привел доказательство теоремы, в которой были сделаны следующие выводы для линеаризованных уравнений:

1. Если все действительные корни характеристического уравнения системы являются отрицательными, то система считается устойчивой.

2. Если хотя бы один действительный корень характеристического уравнения системы положительный, то система считается неустойчивой.

3. Если характеристическое уравнение линеаризованной системы имеет хотя бы один нулевой корень или одну пару мнимых корней, то нельзя судить об устойчивости реальной системы по линеаризованному уравнению.

Следовательно, вывод об устойчивости реальных систем необходимо делать на основе анализа исходного нелинейного уравнения и для определения неустойчивости или устойчивости системы будет достаточно выявить положительность (отрицательность) действительных корней характеристического уравнения.

Критериями устойчивости называют определенные правила, по которым в теории автоматического управления определяют знаки корней характеристического уравнения, не решая его. Различают алгебраические и частотные критерии устойчивости.

Алгебраическими критериями устойчивости системыназывают необходимое и достаточное условие отрицательности корней при определенных значениях коэффициентов в характеристическом уравнении.

Частотными критериями устойчивости системы установлена зависимость устойчивости системы от формы частотных характеристик системы.

Источник