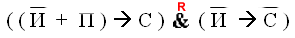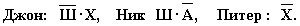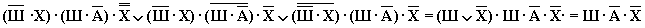Что значит упростить логическое выражение

Что значит упростить логическое выражение

Логические операции (конъюнкция, дизъюнкция, инверсия)

Таблица истинности: К онъюнкция (логическое умножение, логическое И) обозначается /\

(например, А /\ В) либо & (например, А & В); в языках программирования обозначение «And».

Таблица истинности: Дизъюнкция (логическое сложение, логическое ИЛИ) обозначается \/ (например, А \/ В);

в языках программирования обозначение «Or».

Инверсией двух высказываний называется новое высказывание, которое истинное тогда и только тогда, когда исходное высказывание ложно.

Название логической операции

Конъюнкция, логическое умножение

Дизъюнкция, логическое сложение

тогда и только тогда, когда

эквивалентность, эквиваленция, равнозначность

Соединим оба утверждения в одно высказывание:

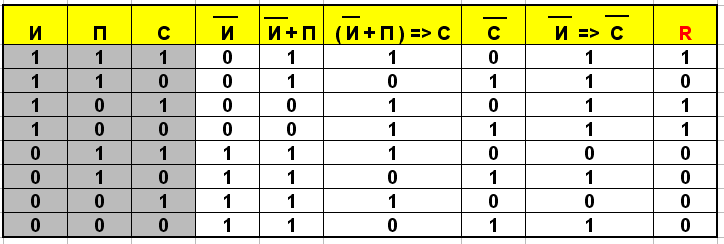
Составим таблицу истинности на полученное высказывание:

Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание

Высказывание 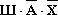истинно только при Ш=1, А=0, Х=0.

Пусть дана таблица истинности для некоторой логической функции Z(X,Y):

Построим истинностную таблицу сложного высказывания :

Очевидно, истинностная таблица будет содержать строк. Скобки применяются, если нарушаются естественный порядок операций: отрицание, конъюнкция, дизъюнкция, импликация, двойная импликация. Скобки (А ® В) указывают на то, что сначала нужно выполнить импликацию, затем найти (А ® В) Ù С. Скобки в выражении можно опустить. Заключительной операцией в построении истинностной таблицы для S будет дизъюнкция двух высказываний: (А ® В) Ù С и .

Источник

Упрощение логических выражений

Для написания любой логической функции может быть использовано логическое выражение, после чего можно составить логическую схему. Как правило, все логические выражения упрощают для получения максимально простой и дешевой логической схемы. В сущности, логическая схема, выражение и логическая функция, являются тремя различными языками, повествующими об одном и том же.

Логические выражения упрощают при помощи различных законов алгебры логики. Часть преобразований напоминает преобразования формул, выполняемые в классической алгебре (например, применение сочетательного и переместительного законов, вынесение за скобки равенства общего множителя и так далее). Для других преобразований используют свойства, которых лишены операции классической алгебры.

Закон двойного отрицания состоит в том, что операция НЕ является обратимой: если ее использовать два раза, логическое значение в результате останется неизменным.

Сущность закона исключенного третьего состоит в том, что каждое логическое выражение при любых условиях является истинным, либо ложным. Если A=1, тогда A=0, а также наоборот. Конъюнкция данных величин всегда равняется 0, дизъюнкция равна 1.

Закон повторения и операции с константами легко можно проверить, используя таблицы истинности операций ИЛИ и И.

Сочетательный и переместительный законы имеют такой же вид, как в математике. Аналогия с привычной всем классической алгеброй.

Для дизъюнкции распределительный закон состоит просто в раскрытии скобок. Для конъюнкции выражение неизвестно, в математике подобное равенство является неверным. Начнем доказывать с правой части. Сначала раскроем скобки:

Используем закон повторение, гласящий, что A⋅A=A,

A+A⋅B=A⋅(1+B)=A⋅1=A, следовательно, (A+B)⋅(A+C)=A+B⋅C.

Мы доказали равенство.

Правил, используемые для раскрытия инверсии сложных выражений, назвали именем известного логика и математика де Моргана. Суть состоит в том, что общее отрицание не только распространяется на отдельные выражения, а еще и дизъюнкция заменяется конъюнкцией (а также наоборот). Для доказательства данных правил используются таблицы истинности.

Основная часть аксиом и законов алгебры логики записаны попарно. Внимательно изучая пары, можно сформулировать принцип двойственности, звучащий следующим образом: если осуществить в тождестве замены конъюнкции, а также дизъюнкции. И также элементов 1 и 0 (при их наличии), получится тождество. Данное свойство именуют принципом двойственности.

Упрощения логических выражений в примерах

Формула, вытекающая из распределительного закона. При ее выведении применили вышеупомянутое правило де Моргана для дизъюнкции, а также использовали закон двойного отрицания, после чего сомножитель X, вынесли за скобку, тогда как в скобках получили закон исключённого третьего, а также применили операцию с константами.

Примеры упрощения логических выражений

Пример первый

Кто из рабочих, обозначенных, как A, B, C, D работает на заводе, а кто нет, если нам даны следующие условия:

Решение задачи. Обозначим несколько простых высказываний:

Сформулировав данные из условия при помощи этих простых высказываний, получим следующее:

Получаем следующую конъюнкцию: ((A+B)→C)⋅(B→C⋅D)⋅C.

После упрощения данной формулы получаем, что A равно 0, B равно 1, C равно 1, D равно 1.

Ответ: ученик A на заводе не работает, а ученики B, C, D играют.

В этом примере применено правило де Моргана, затем использован распределительный закон, после этого применен закон исключенного третьего, потом использован переместительный закон. За ним реализован закон повторения, потом опять применен переместительный закон и, наконец, использован закон поглощения.

Чтобы отыскать решения логического уравнения можно также применить упрощение логических выражений.

Нужно отыскать все решения данного уравнения

Применив правило де Моргана, получим

а затем применяем закон поглощения и получаем

Чтобы логическая сумма равнялась нулю, все слагаемые должны равняться нулю, из чего следует, что

A равно 1, B равно 0, C равно 0, D равно 0.

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Преобразование логических выражений

Информатика. 10 класса. Босова Л.Л. Оглавление

§ 20. Преобразование логических выражений

Способ определения истинности логического выражения путём построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т. к. за счёт существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики.

20.1. Основные законы алгебры логики.

Приведём основные законы алгебры логики.

1. Переместительные (коммутативные) законы:

2. Сочетательные (ассоциативные) законы:

(A v В) v С = A v (В v С).

3. Распределительные (дистрибутивные) законы:

A v (В & С) = (A v В) & (A v С).

4. Законы идемпотентности (отсутствия степеней и коэффициентов):

5. Закон противоречия:

6. Закон исключённого третьего:

7. Закон двойного отрицания:

8. Законы работы с константами:

9. Законы де Моргана:

10. Законы поглощения:

Справедливость законов можно доказать построением таблиц истинности.

Пример 1. Упростим логическое выражение

Последовательно применим дистрибутивный закон и закон исключённого третьего:

Пример 2. Упростим логическое выражение

Аналогичные законы выполняются для операций объединения, пересечения и дополнения множеств. Например:

Пробуйте самостоятельно доказать один из этих законов с помощью кругов Эйлера.

Пример 3. На числовой прямой даны отрезки В = [2; 12] и С = [7; 18]. Каким должен быть отрезок А, чтобы предикат

становился истинным высказыванием при любых значениях х.

Преобразуем исходное выражение, избавившись от импликации:

причём это минимально возможное множество А.

Множество В — это отрезок [2; 12].

Изобразим это графически:

Пересечением этих множеств будет служить промежуток [2; 7[. В качестве ответа мы можем взять этот промежуток, а также любой другой, его включающий.

Чему равна минимальная длина отрезка А? Укажите ещё несколько вариантов множества А.

Пример 4. Для какого наименьшего неотрицательного целого десятичного числа а выражение

тождественно истинно (т. е. принимает значение 1 при любом неотрицательном целом значении десятичной переменной х)? Здесь & — поразрядная конъюнкция двух неотрицательных целых десятичных чисел.

Прежде всего, вспомним, что представляет собой поразрядная конъюнкция двух целых десятичных чисел, например 27 и 22.

Обратите внимание на то, что если в некотором бите хотя бы одного сомножителя есть 0, то 0 есть и в этом бите результата, а 1 в результате получается только тогда, когда в соответствующих битах каждого сомножителя есть 1.

Перепишем исходное выражение в наших обозначениях:

Рассмотрим предикат К(х) = (х & 17 = 0). В числе 17 = 10001₂ 3-й, 2-й и 1-й биты содержат нули, 4-й и 0-й — единицы. Побитовая конъюнкция 17 и х будет равна нулю, если в числе х 4-й и 0-й биты будут содержать нули. Множество истинности этого предиката — все х с нулями в 4-м и 0-м битах.

По условию задачи надо, чтобы

Запишем это выражение для рассмотренных множеств истинности:

Объединением множеств М и N являются все двоичные числа, у которых хотя бы один из битов с номерами 5, 4, 3, 2, 0 содержит единицу. Пересечением этого множества с множеством К будут все двоичные числа, у которых биты с номерами 4 и 0 будут заняты нулями, т. е. такие двоичные числа, у которых хотя бы один из битов с номерами 5, 3, 2 содержит 1. Все эти числа образуют множество А.

Итак, требуемое число 101100₂ или 44₁₀.

Пример 5. Выясним, сколько решений имеет следующая система из двух уравнений:

Конъюнкция истинна тогда и только тогда, когда истинны все образующие её высказывания. Следовательно, каждая из трёх входящих в конъюнкцию импликаций должна быть равна 1.

То же самое проделаем для переменной х₄.

На дереве видно, что рассматриваемое нами уравнение имеет 5 решений — 5 разных наборов значений логических переменных x₁, х₂, х₃, х₄, при которых выполняется равенство:

Следовательно, как и первое уравнение, это уравнение имеет 5 решений. Представим их в табличной форме:

Решение исходной системы логических уравнений — это множество различных наборов значений логических переменных х₁, х₂, х₃, х₄, у₁, у₂, у₃, у₄ таких, что при подстановке каждого из них в систему оба уравнения превращаются в истинные равенства.

Начнём строить такие наборы или двоичные цепочки. Их началом может служить любой из пяти наборов — решений первого уравнения, а концом — любой из пяти наборов — решений второго уравнения. Например, на основе одного из решений первого уравнения можно построить следующие пять решений системы:

Всего мы можем построить 5 • 5 = 25 решений системы.

Вспомните, как называется теорема комбинаторики, которую мы применили для подсчёта количества решений системы.

20.2. Логические функции

Значение любого логического выражения определяется значениями входящих в него логических переменных. Тем самым логическое выражение может рассматриваться как способ задания логической функции.

Совокупность значений п аргументов удобно интерпретировать как строку нулей и единиц длины n. Существует ровно 2 n различных двоичных строк длины n. Так как на каждой такой строке некая функция может принимать значение 0 или 1, общее количество различных булевых функций от n аргументов равно

Для n = 2 существует 16 различных логических функций.

Рассмотрим их подробнее.

С увеличением числа аргументов количество логических функций резко возрастает. Так, для трёх переменных существует 256 различных логических функций! Но изучать их все нет никакой необходимости. Дело в том, что путём преобразований функция любого количества переменных может быть выражена через функции только двух переменных. Более того, можно использовать не все, а лишь некоторые логические функции двух переменных. Например:

1) F₂ и F₁₁ (конъюнкция и отрицание второго аргумента);

2) F₈ и F₁₃ (дизъюнкция и отрицание первого аргумента);

3) F₉ (стрелка Пирса, отрицание дизъюнкции);

4) F₁₅ (штрих Шеффера, отрицание конъюнкции).

Два последних примера говорят о том, что при желании всю алгебру логики можно свести к одной функции! Но чаще всего логические функции записываются в виде логического выражения через отрицание, конъюнкцию и дизъюнкцию.

20.3. Составление логического выражения по таблице истинности и его упрощение

Ранее мы выяснили, что для любого логического выражения можно составить таблицу истинности. Справедливо и обратное: для всякой таблицы истинности можно составить соответствующее ей логическое выражение.

Алгоритм составления логического выражения по таблице истинности достаточно прост. Для этого надо:

1) отметить в таблице истинности наборы переменных, при которых значение логического выражения равно единице;
2) для каждого отмеченного набора записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — её отрицание;
3) все полученные конъюнкции связать операциями дизъюнкции.

Пример 6. Имеется следующая таблица истинности:

После выполнения двух первых шагов алгоритма получим:

После выполнения третьего шага получаем логическое выражение:

Попробуем упростить полученное логическое выражение. Прежде всего, вынесем за скобки В — общий сомножитель, имеющийся у всех трёх слагаемых, затем — сомножитель

, а далее используем законы алгебры логики.

САМОЕ ГЛАВНОЕ

Способ определения истинности логического выражения путём построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т. к. за счёт существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики. Аналогичные законы имеют место и в алгебре множеств.

Логическая функция может быть задана с помощью таблицы истинности или аналитически, т. е. с помощью логического выражения.

Для всякой таблицы истинности можно составить соответствующее ей логическое выражение.

Вопросы и задания

1. Какие из рассмотренных законов алгебры логики аналогичны законам алгебры чисел, а какие нет?

2. Докажите второй закон де Моргана с помощью таблиц истинности.

3. Путём преобразования докажите равносильность следующих высказываний:

4. Упростите логические формулы:

*5. Найдите X,

7. Элементами множеств А, Р и Q являются натуральные числа, причём Р = <2, 4, 6, 8, 10, 12>и Q = <2, 6, 12, 18, 24>.

Известно, что выражение

истинно при любом значении переменной х. Определите наименьшее возможное количество элементов множества А.

*8. На числовой прямой даны два отрезка: М = [10; 60] и N = [40; 80]. Укажите наименьшую возможную длину такого отрезка А, что выражение

истинно при любом значении переменной х.

11. Сколько различных решений имеет система уравнений:

12. Сколько существует различных логических функций от четырёх переменных?

13. По заданной таблице истинности составьте логические выражения для функций F₁, F₂.

14. По известным таблицам истинности запишите аналитическое представление импликации, эквиваленции и строгой дизъюнкции.

15. Логические функции штрих Шеффера и стрелка Пирса названы так в честь математиков, исследовавших их свойства. Подготовьте краткую биографическую справку об одном из этих учёных.

16. По заданной таблице истинности составьте логические выражения для функций F₁, F₂.

17. Запишите логическое выражение для логической функции F(A, В, С), равной 1 на наборах 011, 101, 110, 111. Попытайтесь упростить полученное выражение.

Оглавление

§ 20. Преобразование логических выражений

Источник

Информатика. 10 класс

Конспект урока

Информатика, 10 класс. Урок № 12.

Тема — Преобразование логических выражений

Перечень вопросов, рассматриваемых в теме: основные законы алгебры логики, преобразование логических выражений, логические функции, построение логического выражения с данной таблицей истинности и его упрощение, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ).

Глоссарий по теме: основные законы алгебры логики, логические функции, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ)

Основная литература по теме урока:

Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса

— М.: БИНОМ. Лаборатория знаний, 2017 (с.197—209)

Открытые электронные ресурсы по теме:

Теоретический материал для самостоятельного изучения.

Способ определения истинности логического выражения путем построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т.к. за счет существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики.

Основные законы алгебры логики

Справедливость законов можно доказать построением таблиц истинности.

Пример 1. Упростим логическое выражение

Последовательно применим дистрибутивный закон и закон исключенного третьего:

В общем случае можно предложить следующую последовательность действий:

Пример 2. Упростим логическое выражение .

Здесь последовательно использованы замена операции импликация, закон де Моргана, распределительный закон, закон противоречия и операция с константой, закон идемпотентности и поглощения.

Аналогичные законы выполняются для операции объединения, пересечения и дополнения множеств. Например:

Пример 3. На числовой прямой даны отрезки B = [2;12] и C = [7;18]. Каким должен быть отрезок A, чтобы предикат становился истинным высказыванием при любых значениях x.

Преобразуем исходное выражение, избавившись от импликации:

A, B, C — множества. Для них можно записать (U — универсальное множество).

Будем считать, что.

Тогда , причем это минимально возможное множество А.

Так как множество B — это отрезок [2;12], а множество — это промежутки и, то пересечением этих множеств будет служить промежуток . В качестве ответа мы можем взять этот промежуток, а также любой другой, его включающий.

Пример 4. Для какого наименьшего неотрицательного целого десятичного числа а выражение

тождественно истинно (т. е. принимает значение 1 при любом неотрицательном целом значении десятичной переменной х)? Здесь & — поразрядная конъюнкция двух неотрицательных целых десятичных чисел.

Перепишем исходное выражение в наших обозначениях и преобразуем его:

Рассмотрим предикат . В числе 28₁₀=11100₂ 4-й, 3-й и 2-й биты содержат единицы, а 1-й и 0-й — нули. Следовательно, множеством истинности этого предиката являются такие числа х, у которых хотя бы один из битов с номерами 4, 3 или 2 содержит единицу. Если и 4-й, и 3-й, и 2-й биты числа х нулевые, то высказывание будет ложным.

Рассмотрим предикат . В числе 45₁₀=101101₂ 5-й, 3-й, 2-й и 0-й биты содержат единицы, 4-й и 1-й — нули. Следовательно, множеством истинности этого предиката являются такие числа х, у которых хотя бы один из битов с номерами 5, 3, 2 или 0 содержит единицу. Если и 5-й, и 3-й, и 2-й, и 0-й биты числа х нулевые, то высказывание будет ложным.

Рассмотрим предикат . В числе 17₁₀=10001₂ 3-й, 2-й и 1-й биты содержат нули, 4-й и 0-й — единицы. Побитовая конъюнкция 17 и х будет равна 0, если в числе х 4-й и 0-й биты будут содержать нули. Множество истинности этого предиката — все х с нулями в 4-м и 0-м битах.

По условию задачи надо, чтобы .

Запишем это выражение для рассмотренных множеств истинности:

Так как , примем .

Объединением множеств M и N являются все двоичные числа, у которых хотя бы один из битов с номерами 5, 4, 3, 2, 0 содержит единицу. Пересечением этого множества с множеством K будут все двоичные числа, у которых биты с номерами 4 и 0 будут заняты нулями, т.е. такие двоичные числа, у которых хотя бы один из битов с номерами 5, 3, 2 содержит 1. Все эти числа образуют множество А.

Искомое число a должно быть таким, чтобы при любом неотрицательном целом значении переменной х: , и, кроме того, оно должно быть минимальным из возможных. Этим условиям удовлетворяет число 101100₂ = 44₁₀.

Значение любого логического выражения определяется значениями входящих в него логических переменных. Тем самым логическое выражение может рассматриваться как способ задания логической функции.

Для n=2 существует 16 различных логических функций. Рассмотрим их подробнее.

Источник