Что значит угол 45 градусов в прямоугольном треугольнике
Прямоугольные треугольники
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
Значения тригонометрических функций некоторых углов:
Площадь прямоугольного треугольника равна половине произведения его катетов
Подставим найденное значение в формулу косинуса
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
Прямоугольный треугольник
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).
Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где 
– катеты, 
– гипотенуза. Видеодоказательство
4. Площадь 
прямоугольного треугольника с катетами :
5. Высота 
прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус 
описанной окружности есть половина гипотенузы :
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус 
вписанной окружности выражается через катеты и гипотенузу следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
Кроме того, какова формула тригонометрии?
При этом, какой угол равен 45?
Какой угол равен 45?
Угол можно измерить с помощью транспортира, а угол измерения в 90 градусов называется углом. прямой угол. Под прямым углом две руки перпендикулярны друг другу. Когда прямой угол разделен на две равные части, каждый угол составляет 45 °.
Кто отец тригонометрии?
Первую тригонометрическую таблицу, по-видимому, составил Гиппарх, который, следовательно, теперь известен как «отец тригонометрии».
Где используется тригонометрия?
Другие применения тригонометрии:
Это использовано в океанографии при расчете высоты приливов в океанах. Функции синуса и косинуса являются фундаментальными для теории периодических функций, описывающих звуковые и световые волны. Исчисление состоит из тригонометрии и алгебры.
Какая формула Sinx?
Угол сдвига на π / 2, π, 3π / 2 (тождества ко-функции или тождества периодичности)
Сколько углов 45 CIRC 45 ∘ 45 градусов нужно, чтобы сделать полный поворот?
Ответ: Требуется восемь 45 углы градусов, чтобы сделать полный поворот.
Полный поворот означает разворот до тех пор, пока он снова не будет указывать в том же направлении.
Что такое правило планирования под углом 45 градусов?
Правило 45 градусов оценивается как на плане, так и на высоте. Пристройка не должна выходить за линию, проведенную под углом 45 градусов от центра ближайшего окна первого этажа жилого помещения на прилегающей территории..
В какое время солнце находится под углом 45 градусов?
На полюсах солнце ходит кругами над или под горизонтом. На 45 градусах широты солнце встает и заходит примерно в 45 градусов к горизонту в дни равноденствия. Это 10.6 градуса вверх и 10.6 градуса в сторону в час. Это неверно около полудня.
Каковы характеристики треугольника 45 45 90?
45−45−90 относится к углам треугольника.
Каковы длины сторон треугольника 45 45 90?
Как соотносятся гипотенуза и катет треугольника 45 45 90?
Какой угол составляет 45 градусов и 135 градусов?
Как еще называют 45 45 90?
Кто первым изобрел тригонометрию?
Тригонометрия в современном понимании началась с греков. Гиппарх (ок. 190–120 до н. э.) был первым, кто построил таблицу значений тригонометрической функции.
Кто отец нуля?
Первый современный эквивалент цифры ноль происходит от Индуистский астроном и математик Брахмагупта в 628 году. Его символом для изображения числа была точка под числом. Он также написал стандартные правила для достижения нуля с помощью сложения и вычитания, а также результаты операций, которые включают цифру.
Кто изобрел тригонометрическую таблицу?
Греческий астроном Гиппарх (DC 127 г. до н.э.) был первым, кто составил таблицу тригонометрических функций (на основе хорд в круге), которые он вычислял с шагом 7 ° 30 ′.
Что такое тригонометрия?
Тригонометрия, филиал математики, связанной с конкретными функциями углов и их применением в вычислениях. В тригонометрии обычно используются шесть функций угла. Их имена и сокращения: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc).
Как вы вводите тригонометрию?
Знакомство с тригонометрией
Сколько существует видов тригонометрии?
В математике всего шесть разных типов тригонометрических функций: синус (sin), косинус (cos), секанс (сек), косеканс (косеканс), тангенс (tan) и котангенс (cot). Эти шесть различных типов тригонометрических функций символизируют соотношение между соотношениями сторон прямоугольного треугольника.
Что такое формула sin3x?
Какова формула Tan2x?
Tan2x =2tanx / 1-загар ^ 2x.
Какова формула 2SINXCOSX?
Значение тригонометрических функций углов 30°, 45° и 60°
Найдем значение Sin, Cos, Tg, Ctg трёх примечательных углов 30°, 45° и 60°.
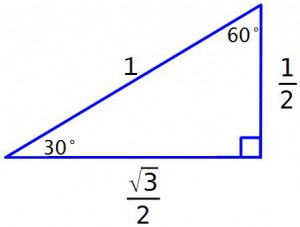
30° и 60°
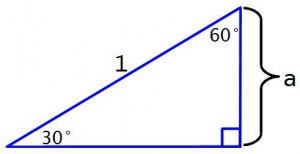
Начнём с синуса 30°. Для этого построим прямоугольный треугольник с острым углом в 30°. И синус 30° – это будет отношение противолежащего короткого катета к гипотенузе. И для удобства установим длину гипотенузы единица.
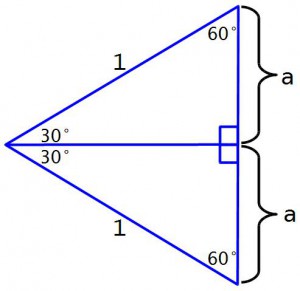
И тогда получается что отношение длины катета к гипотенузе равно просто длине катета, и синус 30° будет равен просто а. Кроме того, сумма углов любого треугольника равна 180°, и 2й острый угол равен 180° – 90° – 30° = 60°. И для 2го острого угла отношение короткого катета к гипотенузе – это будет отношение прилежащего катета к гипотенузе то есть косинус. И значит, Cos(60°) тоже будет равен а. А теперь найдем, чему же равно это а. Для этого построим снизу ещё один такой же треугольник, равный исходному — только отраженный зеркально.
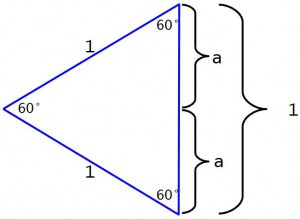
И вот что получается: во-первых приглядимся к углу, сложившемуся из двух прямых углов – он развернутый. Получается, что верхняя и нижняя точки треугольника и вершина прямых углов лежат на одном отрезке. А левый угол складывается из двух углов по 30°, то есть равен он 60°. Следовательно, можно стереть горизонтальный отрезок, и получается треугольник, у которого каждый угол равен 60°.
Равносторонний треугольник, у которого третья сторона равна первым двум сторонам и тоже равна единице. Получилось, что:
А это означает, что
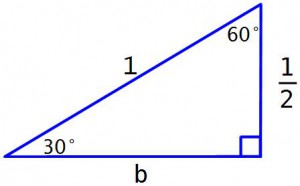
Теперь вернемся к исходному треугольнику. Короткий катет теперь известен – это 1/2. А чему же равен длинный катет? Обозначим его буквой b.
Для угла в 30° этот катет b – прилежащий, гипотенуза равна 1. И значит длина этого катета равна отношению длины прилежащего катета к гипотенузе, то есть Cos(30°). А для 60° этот длинный катет – противолежащий. И следовательно длина этого катета равна отношению противолежащего катета к гипотенузе, то есть Sin(60°). И значит
Ну а теперь найдем катет b с помощью теоремы Пифагора. Как известно, сумма квадратов катетов равна квадрату гипотенузы, то есть
Теперь уже известны оба катета, и можно найти отношение двух катетов. Сначала найдём отношение короткого катета к длинному катету. Для угла в 30° это будет отношение противолежащего катета к прилежащему катету, то есть Tg(30°). А для угла в 60° это будет наоборот – отношение прилежащего катета к противолежащему катету то есть Ctg(60°).
А теперь наоборот длинный катет разделим на короткий катет. Для 30° это будет прилежащий катет разделить на противолежащий, то есть Ctg(30°). А для 60° это будет противолежащий катет разделить на прилежащий, то есть Tg(60°).
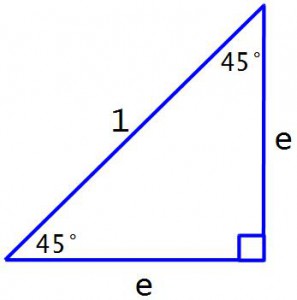
Построим прямоугольный треугольник с острым углом 45 градусов. Гипотенузу опять сделаем единицу и противолежащий катет обозначим буквой e.
Отношение противолежащего катета к гипотенузе и будет равно Sin(45°). Но гипотенуза – единица – поэтому просто длина этого катета равна синусу Sin(45°). Теперь обратим внимание на 2й острый угол. На два острых угла в прямоугольном треугольнике приходится 90°. Значит 2й острый угол равен 90° – 45° = 45°. Выходит что этот прямоугольный треугольник – равнобедренный, и второй катет тоже равен е. И получается что для угла 45° отношение прилежащего катета к гипотенузе такое же, как и противолежащего катета к гипотенузе
Кроме того, даже не зная, чему равно е, можно сказать, какой будет Tg(45°) и Ctg(45°), потому что отношение противолежащего катета к прилежащему или, наоборот, прилежащего катета к противолежащему – будет равно единице.
Tg(45°) = Ctg(45°) = e / e = 1
Ну а теперь можно уже наконец найти, чему равно е. И для этого воспользуемся теоремой Пифагора.
И таким образом найдены значения основных тригонометрических функций углов 30° 45° и 60°.