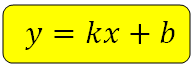Что значит угловой коэффициент прямой
Угловой коэффициент.
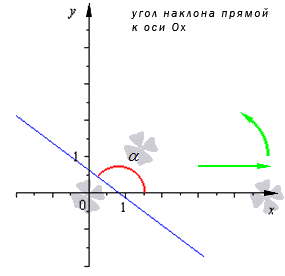
Угловой коэффициент— коэффициент k в уравнении прямой на плоскости y = kx + b. Он численно равняется тангенсу угла между выбранной прямой и осью 0х. Этот угол отсчитывается от положительного направления оси 0х до прямой против хода часовой стрелки и располагается и пределах от 0 до 180 градусов.
Для обозначения углового коэффициента употребляют латинский символ k. И, основываясь на определении получаем:
Когда прямая параллельна оси 0х или совпадает с ней, то угол ее наклона расценивают, как равный нулю.
Когда прямая параллельна оси 0у, то угловой коэффициент отсутствует и принято указывать, что угловой коэффициент обращается в бесконечность.
Положительный угловой коэффициент прямой свидетельствует о росте графика функции, отрицательный угловой коэффициент – об убывании.
Угловой коэффициент прямой так же есть возможность вычислить, когда установлены координаты двух произвольных точек прямой:
Тогда, в образовавшемся прямоугольном треугольнике M1РM2 вычисляем тангенс:
Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Уравнение с угловым коэффициентом
Ответ: М 1 принадлежит прямой, а М 2 нет.
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Решение
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
Решим задачу обратную данной.
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
График линейной функции, его свойства и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
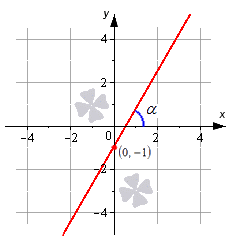
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Угловой коэффициент прямой
Угловой коэффициент прямой — коэффициент 

Тангенс угла может рассчитываться как отношение противолежащего катета к прилежащему. k всегда равен 
При положительных значениях углового коэффициента k и нулевом значении коэффициента сдвига b прямая будет лежать в первом и третьем квадрантах (в которых x и y одновременно положительны и отрицательны). При этом большим значениям углового коэффициента k будет соответствовать более крутая прямая, а меньшим — более пологая.
Прямые 



Примечания
Полезное
Смотреть что такое «Угловой коэффициент прямой» в других словарях:
угловой коэффициент (прямой) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN slope … Справочник технического переводчика
Угловой коэффициент — (математическое) число k в уравнении прямой линии на плоскости у = kx+b (см. Аналитическая геометрия), характеризующее наклон прямой относительно оси абсцисс. В прямоугольной системе координат У. к. k = tg φ, где φ угол между… … Большая советская энциклопедия
Уравнения прямой — Изображение прямых в прямоугольной системе координат Прямая одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется… … Википедия
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ — раздел геометрии, который исследует простейшие геометрические объекты средствами элементарной алгебры на основе метода координат. Создание аналитической геометрии обычно приписывают Р.Декарту, изложившему ее основы в последней главе своего… … Энциклопедия Кольера
Время реакции (reaction time) — Измерение времени реакции (ВР), вероятно, самый почтенный предмет в эмпирической психологии. Оно зародилось в области астрономии, в 1823 г., с измерением индивидуальных различий в скорости восприятия пересечения звездой линии риски телескопа. Эти … Психологическая энциклопедия
МАТЕМАТИЧЕСКИЙ АНАЛИЗ — раздел математики, дающий методы количественного исследования разных процессов изменения; занимается изучением скорости изменения (дифференциальное исчисление) и определением длин кривых, площадей и объемов фигур, ограниченных кривыми контурами и … Энциклопедия Кольера
Прямая — У этого термина существуют и другие значения, см. Прямая (значения). Прямая одно из основных понятий геометрии, то есть точного универсального определения не имеет. При систематическом изложении геометрии прямая линия обычно принимается за одно… … Википедия
Прямая линия — Изображение прямых в прямоугольной системе координат Прямая одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется… … Википедия
Прямые — Изображение прямых в прямоугольной системе координат Прямая одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется… … Википедия
Малая полуось — Не следует путать с термином «Эллипсис». Эллипс и его фокусы Эллипс (др. греч. ἔλλειψις недостаток, в смысле недостатка эксцентриситета до 1) геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний от двух данных точек F1… … Википедия
Угловой коэффициент прямой (и не только)!
Угловой коэффициент прямой. В этой статье мы с вами рассмотрим задачи связанные с координатной плоскостью включённые в ЕГЭ по математике. Это задания на:
— определение углового коэффициента прямой, когда известны две точки через которые она проходит;
— определение абсциссы или ординаты точки пересечения двух прямых на плоскости.
Что такое абсцисса и ордината точки было описано в прошлой статье данной рубрики. В ней мы уже рассмотрели несколько задач связанных с координатной плоскостью. Что необходимо понимать для рассматриваемого типа задач? Немного теории.
Уравнение прямой на координатной плоскости имеет вид:
где k – это и есть угловой коэффициент прямой.
Следующий момент! Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох.
Он лежит в пределах от 0 до 180 градусов.
То есть, если мы приведём уравнение прямой к виду y = kx + b, то далее всегда сможем определить коэффициент k (угловой коэффициент).
Так же, если мы исходя из условия сможем определить тангенс угла наклона прямой, то тем самым найдём её угловой коэффициент.
Следующий теоретический момент! Уравнение прямой походящей через две данные точки. Формула имеет вид:
Рассмотрим задачи (аналогичные задачам из открытого банка заданий):
Найдите угловой коэффициент прямой, проходящей через точки с координатами (–6;0) и (0;6).
В данной задаче самый рациональный путь решения это найти тангенс угла между осью ох и данной прямой. Известно, что он равен угловому коэффициенту. Рассмотрим прямоугольный треугольник образованный прямой и осями ох и оу:
Тангенсом угла в прямоугольном треугольнике является отношение противолежащего катета к прилежащему:

Конечно, данную задачу можно решить используя формулу нахождения уравнения прямой проходящей через две данные точки. Но это будет более длительный путь решения.
Найдите угловой коэффициент прямой, проходящей через точки с координатами (5;0) и (0;5).
Формула уравнения прямой походящей через две данные точки имеет вид:
Наши точки имеют координаты (5;0) и (0;5). Значит,
Получили, что угловой коэффициент k = – 1.
Прямая a проходит через точки с координатами (0;6) и (8;0). Прямая b проходит через точку с координатами (0;10) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.
В данной задаче можно найти уравнение прямой a, определить угловой коэффициент для неё. У прямой b угловой коэффициент будет такой же, так как они параллельны. Далее можно найти уравнение прямой b. А затем, подставив в него значение y = 0, найти абсциссу. НО!
В данном случае, проще использовать свойство подобия треугольников.
Прямоугольные треугольники, образованные данными (параллельными) прямыми о осями координат подобны, а это значит, что отношения их соответствующих сторон равны.
Искомая абсцисса равна 40/3.
Прямая a проходит через точки с координатами (0;8) и (–12;0). Прямая b проходит через точку с координатами (0; –12) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.
Для данной задачи самый рациональный путь решения — это применение свойства подобия треугольников. Но мы решим её другим путём.
Нам известны точки, через которые проходит прямая а. Можем составить уравнение прямой. Формула уравнения прямой походящей через две данные точки имеет вид:
По условию точки имеют координаты (0;8) и (–12;0). Значит,
Получили, что угловой k = 2/3.
*Угловой коэффициент можно было найти через тангенс угла в прямоугольном треугольнике с катетами 8 и 12.
Известно, у параллельных прямых угловые коэффициенты равны. Значит уравнение прямой проходящей через точку (0;-12) имеет вид:
Найти величину b мы можем подставив абсциссу и ординату в уравнение:
Таким образом, прямая имеет вид:
Теперь чтобы найти искомую абсциссу точки пересечения прямой с осью ох, необходимо подставить у = 0:
Найдите ординату точки пересечения оси оy и прямой, проходящей через точку В(10;12) и параллельной прямой, проходящей через начало координат и точку А(10;24).
Найдём уравнение прямой проходящей через точки с координатами (0;0) и (10;24).
Формула уравнения прямой походящей через две данные точки имеет вид:
Наши точки имеют координаты (0;0) и (10;24). Значит,
Угловые коэффициенты параллельных прямых равны. Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:
Значение b найдём подставив в это уравнение координаты точки В(10;12):
Получили уравнение прямой:
Чтобы найти ординату точки пересечения этой прямой с осью оу нужно подставить в найденное уравнение х = 0:
*Самый простой способ решения. При помощи параллельного переноса сдвигаем данную прямую вниз вдоль оси оу до точки (10;12). Сдвиг происходит на 12 единиц, то есть точка А(10;24) «перешла» в точку В(10;12), а точка О(0;0) «перешла» в точку (0;–12). Значит, полученная прямая будет пересекать ось оу в точке (0;–12).
Искомая ордината равна –12.
Найдите ординату точки пересечения прямой, заданной уравнением
Координата точки пересечения заданной прямой с осью оу имеет вид (0;у). Подставим в уравнение абсциссу х = 0, и найдём ординату:
Ордината точки пересечения прямой с осью оу равна 3.
Найдите ординату точки пересечения прямых, заданных уравнениями
Когда заданны две прямые, и стоит вопрос о нахождении координат точки пересечения этих прямых, решается система из данных уравнений:
В первом уравнении подставляем – х вместо у:
Ордината равна минус шести.
Найдите угловой коэффициент прямой, проходящей через точки с координатами (–2;0) и (0;2).
Найдите угловой коэффициент прямой, проходящей через точки с координатами (2;0) и (0;2).
Прямая a проходит через точки с координатами (0;4) и (6;0). Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.
Прямая a проходит через точки с координатами (0;4) и (–6;0). Прямая b проходит через точку с координатами (0; –6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.
Найдите ординату точки пересечения оси оy и прямой, проходящей через точку B (6;4) и параллельной прямой, проходящей через начало координат и точку A (6;8).
Найдите абсциссу точки пересечения прямой, заданной уравнением 2х + 2у = 6, с осью ох.
Найдите абсциссу точки пересечения прямых, заданных уравнениями 3х + 2у = 6 и у = х.
Конечно, некоторые задачи, которые мы рассмотрели можно было решить более рациональными способами. Но ставилась цель показать разные подходы к решению. Надеюсь, это удалось.
1. Необходимо чётко усвоить, что угловой коэффициент прямой равен тангенсу угла наклона прямой. Это поможет вам при решении многих задач данного типа.
2. Формулу нахождения прямой проходящей через две данные точки нужно понимать обязательно. С её помощью всегда найдёте уравнение прямой, если даны координаты двух её точек.
3. Помните о том, что угловые коэффициенты параллельных прямых равны.
4. Как вы поняли, в некоторых задачах удобно использовать признак подобия треугольников. Задачи решаются практически устно.
5. Задачи в которых даны две прямые и требуется найти абсциссу или ординату точки их пересечения можно решить графическим способом. То есть, построить их на координатной плоскости (на листе в клетку) и определить точку пересечения визуально. *Но этот способ применим не всегда.
6. И последнее. Если дана прямая и координаты точек её пересечения с осями координат, то в таких задачах удобно находить угловой коэффициент через нахождение тангенса угла в образованном прямоугольном треугольнике. Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:
>> Угол наклона прямой от 0 до 90 градусов
>> Угол наклона прямой от 90 до 180 градусов
В данных двух случаях, по свойству тангенса :
То есть, чтобы найти уголвой коэффициент прямой, необходимо вычислить тангенс бетта в полученном прямоугольном треугольнике и записать результат с отрицательным знаком.
В данной рубрике продолжим рассматривать задачи, не пропустите!