Что значит тождественно истинно
ТОЖДЕСТВЕННО ИСТИННЫЕ И ТОЖДЕСТВЕННО ЛОЖНЫЕ ВЫСКАЗЫВАНИЯ
· приоритет логических операций;
· тождественно истинные и тождественно ложные операции;
· основные законы алгебры логики;
· доказательство логических законов;
· простейшие преобразователи информации;
Если сложное высказывание истинно для всех значений входящих в него переменных, то такое высказывание называется ТОЖДЕСТВЕННО ИСТИННЫМ или тавтологией (обозначается константой 1).
Все математические, физические и др. законы являются тавтологиями. Например: (а+b) 2 = a 2 + 2ab + b 2
Прогноз погоды на завтра может быть, например, таким: «Дождь будет или дождя не будет». Такое предсказание будет всегда истинным, хотя вряд ли кого устроит. Его математическая запись:
(по закону исключенного третьего всегда должно быть истинным либо суждение, либо его отрицание).
Проверить, является ли сложное высказывание тождественно истинным, можно по таблице истинности.
Если сложное высказывание ложно при всех значениях входящих в него переменных, то такое высказывание называется ТОЖДЕСТВЕННО ЛОЖНЫМ (обозначается константой 0 ).
(по закону противоречия: не могут быть одновременно истинны утверждение и его отрицание.)
Если значения сложных высказываний совпадают при всех возможных значениях входящих в них переменных, то такие высказывания называют РАВНОСИЛЬНЫМИ, ТОЖДЕСТВЕННЫМИ, ЭКВИВАЛЕНТНЫМИ
ОСНОВНЫЕ ЗАКОНЫ (РАВНОСИЛЬНОСТИ) АЛГЕБРЫ ЛОГИКИ
· приоритет логических операций;
· тождественно истинные и тождественно ложные операции;
· основные законы алгебры логики;
· доказательство логических законов;
· простейшие преобразователи информации;
При решении логических задач часто приходится упрощать формулы. Упрощение формул в булевой алгебре производится на основе эквивалентных преобразований, опирающихся на основные законы.
1.1. Закон тождества:
— всякая мысль тождественна самой себе, то есть «А есть А», где А – любое высказывание.
2. Закон исключенного третьего:
— в один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Истинно либо А, либо не А.
НАПРИМЕР. «Число 123 либо четное, либо нечетное, третьего не дано».
Закон исключенного третьего не является законом, признаваемым всеми логиками в качестве универсального закона логики. Этот закон применяется там, где познание имеет дело с жесткой ситуацией: либо-либо, истина-ложь. Там же где встречается неопределенность (например, в рассуждениях о будущем), закон исключенного третьего часто не может быть применен.
Рассмотрим следующее высказывание: «Это предложение ложно». Оно не может быть истинным, потому, что оно утверждает, что оно ложно. Но оно не может быть и ложным, потому что тогда оно было бы истинным. Это высказывание не истинно и не ложно, а потому нарушается закон исключенного третьего.
«В одном городе парикмахер стрижет волосы всем жителям, кроме тех, кто стрижет себя сам. Кто стрижет волосы парикмахеру?»
В нашей формальной системе нет возможности ввести такое ссылающееся само на себя истолкование, поэтому мы не можем выразить все возможные мысли и доводы.
3. Закон непротиворечия:
Именно эта формула часто используется при упрощении сложных логических выражений.
Иногда этот закон формулируется так: два противоречащих друг другу высказывания не могут быть одновременно истинными.
ПРИМЕР. Е = «На Марсе есть жизнь и на Марсе жизни нет»
4. Закон двойного отрицания:
— если отрицать дважды некоторое высказывание, то в результате получается исходное высказывание.
НАПРИМЕР: А = «Неверно, что Матроскин не кот»
Равносильные формулы алгебры высказываний
Равносильные формулы алгебры высказываний
Равносильные формулы алгебры высказываний
Например, равносильны формулы:
Тождественно истинная формула
Тождественно ложная формула
Выполнимая формула
Ясно, что отношение равносильности рефлексивно, симметрично и транзитивно.
Группы равносильностей
Важнейшие равносильности алгебры высказываний можно разбить на следующие группы.
Равносильности алгебры Буля
Равносильности, выражающие одни логические операции через другие
$X\leftrightarrow Y\equiv (X\rightarrow Y)\wedge (Y\rightarrow X)$
$X\leftrightarrow Y\equiv (\overline < X >\vee Y)\wedge (\overline < Y >\vee X)$
$X\leftrightarrow Y\equiv (X\wedge Y)\wedge (\overline < Y >\wedge \overline < X >)$
$X\rightarrow Y\equiv \overline < X >\vee Y$
$X | Y\equiv \overline < X\cdot Y >$
$X \downarrow Y\equiv \overline < X\vee Y >$
$X \rightarrow Y\equiv \overline < X >\vee Y$
$X \bigoplus Y\equiv (X \cdot \bar < Y >)\vee (\bar < X >\cdot Y)$
$X \sim Y\equiv \overline < X \bigoplus Y >\equiv (XY)\vee (\bar < X >\bar < Y >)$
Далее:
Теорема об алгоритме распознавания полноты
Поверхностный интеграл первого рода и его свойства
Свойства тройного интеграла
Несобственные интегралы от неограниченной функции
Упрощение логических функций
Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы
Определение тройного интеграла. Теорема существования тройного интеграла
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Нормальные формы
Теорема Остроградского
Полином Жегалкина. Пример.
Вычисление двойного интеграла. Двукратный интеграл
Вычисление криволинейного интеграла второго рода. Примеры.
Алгебра логики
Алгебра логики — раздел математики, изучающий высказывания с точки зрения их логических значений (истинности или ложности) и логических операций над ними.
Иногда ее называют двоичной логикой или булевой алгеброй по имени английского математика Джорджа Буля.
Для удобства записи, используют обозначение результата через F, а логические высказывания через A (X) и B (Y). Так как возможных вариантов значений всего два, их можно обозначить через 0 (ложь, нет, false, no) и 1 (истина, да, true, yes).
Таблица истинности — табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
Логическое высказывание
Логическое высказывание — любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Тождественно истинные высказывания (тавтология)
Тождественно истинными называются высказывания, истинные при любых значениях входящих в него переменных.
Таким образом, такое высказывание всегда равно 1.
В качестве примеров можно привести высказывания, являющиеся разъяснением термина на основе его словообразования (авиабаза — место базирования авиационной техники). Или любое сложное высказывание, смысл которого сводится к формуле А \/ ¬A.
Тождественно ложные высказывания
Тождественно ложными называются высказывания, ложные при любых значениях входящих в него переменных.
Таким образом, такое высказывание всегда равно 0.
Важно, что большинство высказываний сводится к формуле А /\ ¬A.
Эквивалентные высказывания
Эквивалентными (тождественными или равносильными) называются высказывания, значения которых совпадают при любых значениях входящих в него переменных.
Логические операции
Логическое умножение (конъюнкция)
Представляет собой объединение нескольких логических выражений с помощью союза И. При практическом наборе на компьютере часто используют знаки прямого и обратного деления без пробела: /\
Таким образом, все значения должны быть истинными: И первое, И второе, И. При умножении логических операторов мы получим единицу только если все они будут равны единице:
| A | B | F = A & B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Отсюда вытекает обратное следствие, упрощающее вычисления для конъюнкции:
Если хотя бы одно значение ложно, то ложно и всё выражение.
Логическое сложение (дизъюнкция)
Представляет собой объединение логических выражений с помощью союза ИЛИ. Если при сложении результат становится больше нуля, то он выражается единицей. При практическом наборе на компьютере часто используют знаки обратного и прямого деления без пробела: \/
| A | B | F = A \/ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Отсюда вытекает обратное следствие, упрощающее вычисления для дизъюнкции:
Если хотя бы одно значение истинно, то истинно и всё выражение.
Логическое отрицание (инверсия)
Представляет собой логическое выражение с добавленной в начале частицей НЕ. То есть операция всегда обращает значение в противоположное.
| A | F = ¬A |
| 0 | 1 |
| 1 | 0 |
Логическое следование (импликация)
Связывает два логических выражения с помощью оборота ЕСЛИ. ТО.
Дополнительная операция, так как A → B = 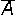
Кроме того, при построении высказывания могут использоваться выражения «из. следует», «. влечет».
| A | B | F = A → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
В таблице хорошо видна практическая суть: импликация ложна только тогда, когда первое выражение истинно, а второе ложно.
При решении задач, в большинстве случаев требуется применение закона снятия импликации.
Логическое равенство (эквивалентность)
Образуется соединением двух логических выражений с помощью оборотов «тогда и только тогда», «необходимо и достаточно», «. равносильно. ». Поскольку мы видим здесь двойное следование (и вправо и влево), операцию иногда называют двойной импликацией. Дополнительная операция, так как A ↔ B = (A ∨ 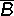
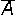
| A | B | F = A ↔ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Суть: эквивалентность ложна только тогда, когда выражения разные.
Законы алгебры логики
Те, кому лень учить эти законы, должны вспомнить алгебру, где знание нескольких способов преобразования позволяет решать очень сложные уравнения.
Строго говоря, это не законы, а теоремы. Но их доказательство не входит в программу изучения. Впрочем, доказательство обычно основывается на построении полной таблицы истинности.
Замечание. Знаки алгебры логики намеренно заменены на сложение и умножение.
| № | Для ИЛИ | Для И | Примечание |
| 1 | A + 0 = A | A • 1 = A | Ничего не меняется при действии, константы удаляются |
| 2 | A + 1 = 1 | A • 0 = 0 | Удаляются переменные, так как их оценивание не имеет смысла |
| 3 | A + B = B + A | AB = BA | Переместительный (коммутативности) |
| 4 | A + 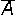 = 1 = 1 | Один из операторов всегда 1 (закон исключения третьего) | |
| 5 | A • 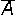 = 0 = 0 | Один из операторов всегда 0 (закон непротиворечия) | |
| 6 | A + A = A | A • A = A | Идемпотентности (NB! Вместо A можно подставить составное выражение!) |
| 7 | ¬¬A = A | Двойное отрицание | |
| 8 | (A+B)+C = A+( B+C) | (A•B)•C = A•(B•C) | Ассоциативный |
| 9 | (A+B)•C = = (A•C)+( B•C) | (A•B)+C = = (A+C)•( B+C) | Дистрибутивный |
| 10 | (A+B)•(¬A+B) = B | (A•B)+(¬A•B) = B | Склеивания |
| 11 | ¬(A+B) = ¬A•¬ B | ¬(A•B) = ¬A+¬ B | Правило де Моргана |
| 12 | A+(A•C) = A | A•(A+C) = A | Поглощение |
| 13 | A→B = ¬A+ B и A→B = ¬B→ ¬A | Снятие (замена) импликации | |
| 14 | 1) A↔B = (A•B)+(¬A•¬ B) 2) A↔B = (A + ¬B)•(¬A + B) | Снятие (замена) эквивалентности | |
Порядок решения логического выражения
В первую очередь надо учитывать, что порядок задается скобками.
Далее выполняются операции отрицания, конъюнкции, дизъюнкции, импликации, эквивалентности.
Построение таблиц истинности
Чтобы решить логическое выражение, необходимо построить таблицу истинности, описывающую ВСЕ возможные варианты значений переменных величин. В связи с тем, что мы используем булевы переменные (то есть имеющие только два значения: 0 и 1), количество вариантов легко сосчитать по формуле
где N — число переменных, а M — число строк в результирующей таблице.
Заполнение же значений фактически является последовательным вписыванием в каждой строке двоичных чисел. Для первой строки это будет 0 (00, 000. ), для второй — 1 (01, 001. ), а для последней — числа, состоящего из всех единиц. Выполнение этого несложного правила позволит не только избежать ошибок, но и облегчит решение, так как значения 0/1 будут подчиняться определенному порядку для каждой переменной.
Графическое решение числовых выражений по координатной прямой
Ряд заданий в алгебре логики основывается в использовании в качестве высказывания числового выражения. Например,
Хорошо видно, что выражение берется в скобки для однозначного восприятия. Прежде чем наносить значения на рисунок, следует избавиться от отрицания. В этом случае происходит замена знаков отношения на противоположные по схеме: ↔ ≤, = ↔ ≠.
В нашем примере мы получим
Нанесем два значения на координатную прямую и, учитывая логическое И, у нас должны совпасть оба условия. То есть на прямой это будет пересечение, обозначенное красным.
Возможные целочисленные ответы — 3, 4, 5.
Построение логического выражения по таблице истинности
Задача является противоположной стандартной.
При ее решении нужно построить дизъюнкцию для всех строк, равных 1, то есть составить выражение в дизъюнктивной нормальной форме (ДНФ).
Решение текстовых задач
На предыдущих этапах, в частности, изучались графический и табличный способы, которые невозможно, либо чрезмерно трудоемко использовать для сложных заданий. Также, решение задач путем рассуждений зачастую неэффективно.
Многие учащиеся очень расстраиваются, что, используя ранее эти способы, они тратили много времени на то, чтобы выработать стратегию, правильно понимать задание и т.п. А теперь их удается решить буквально за несколько секунд. Эта позиция неверна. Большинство подобных задач в реальной жизни не содержит достаточных сведений для решения средствами алгебры логики. Умение анализировать данные и находить «пробелы» в исходных данных — намного важнее.
При решении логической задачи средствами алгебры логики, необходимо выделить из текста логические условия и записать их в виде выражения.
Каждое высказывание оформляется в виде логической переменной. Чаще всего удобно вводить переменные, обозначенные русскими буквами и связанные с объектами, описанными в задаче: Иван — И, красный — К (или Кр, если переменная К уже введена для Коли) и т.п.
В большинстве случаев потребуется упрощение выражения с использованием законов алгебры логики.
В некоторых случаях удобно составить систему высказываний (аналогично системе уравнений) и, затем, решать уже её.
Логическое значение категорически рекомендуется записывать как 0 (ложь) или 1 (истина). Это поможет дифференцировать записи, а не спотыкаться о глупейшие варианты Л/И.
Введем обозначения для логических высказываний:
Л — победит Ласточка; С — победит Стрела; Т — победит Тормоз.
Запишем высказывания (высказывание Петра «Тормоз готовился очень тщательно» не содержит информации о месте и не может быть учтено):
Учитывая истинность предположений двух друзей и ложность третьего, запишем истинное высказывание, основанное на том, что неправ либо первый, либо второй, либо третий:
Затем упростим его за счет двойного отрицания, правила Моргана и убрав ненужные для первого члена скобки:
[¬Л /\ С /\ Л /\ ¬Т /\ С] \/ [(Л \/ ¬С) /\ (¬Л \/ Т) /\ ¬С] \/ [(Л \/ ¬С) /\ (Л /\ ¬Т) /\ ¬С] = 1
Выражение по-прежнему немаленькое. Далее, по закону поглощения можно сократить показанное красным
[ ¬Л /\ С /\ Л /\ ¬Т /\ С] \/ [ (Л \/ ¬С) /\ (¬Л \/ Т) /\ ¬С ] \/ [ (Л \/ ¬С) /\ (Л /\ ¬Т) /\ ¬С ] = 1
[(¬Л \/ Т) /\ ¬С] \/ [(Л /\ ¬Т) /\ ¬С] = 1
В оставшейся части сократим противоположные слагаемые (по закону исключения третьего)
Конечно, можно сразу сказать, что в произведении все три множителя должны быть равны единице, то есть: Л = 1, Т = 0, С = 0. Ответ: победителем скачек стала Ласточка.
Но можно сделать то же, построив таблицу истинности:
ТОЖДЕСТВЕННАЯ ИСТИННОСТЬ
Полезное
Смотреть что такое «ТОЖДЕСТВЕННАЯ ИСТИННОСТЬ» в других словарях:
ТОЖДЕСТВЕННАЯ ИСТИННОСТЬ — свойство сложных высказываний быть истинными в силу своей формально логической структуры и смысла используемых в них логических операций. Будучи независимыми от содержания входящих в них конкретных высказываний, тождественно истинные высказывания … Большой Энциклопедический словарь
ТОЖДЕСТВЕННАЯ ИСТИННОСТЬ — логическая истинность, общезначимоеть, свойство формул языка исчисления предикатов, означающее истинность формулы во всех ее интерпретациях и цри всех допустимых значениях ее свободных переменных. Так, для формул, содержащих только один… … Математическая энциклопедия
тождественная истинность — свойство сложных высказываний быть истинными в силу своей формально логической структуры и смысла используемых в них логических операций. Будучи независимыми от содержания входящих в них конкретных высказываний, тождественно истинные высказывания … Энциклопедический словарь
Тождественная истинность — свойство сложных высказываний (См. Высказывание), истинных в силу их формально логической структуры и смысла (интерпретации) входящих в них логических операций. Такие высказывания лишь «по видимости» описывают факты (классы фактических… … Большая советская энциклопедия
ТОЖДЕСТВЕННАЯ ИСТИННОСТЬ — свойство сложных высказываний быть истинными в силу своей формально логич. структуры и смысла используемых в них логич. операций. Будучи независимыми от содержания входящих в них конкретных высказываний, тождественно истинные высказывания… … Естествознание. Энциклопедический словарь
ФАКТИЧЕСКАЯ ИСТИННОСТЬ — (в л о г и к е) – истинность предложения (суждения, высказывания), обусловленная, в отличие от т.н. логич. истинности, содержанием этого предложения. Иначе говоря, предложение является фактически истинным, когда его истинность зависит от значений … Философская энциклопедия
тавтология — и; ж. [от греч. tauto то же самое и logos слово] 1. Повторение того же самого другими словами, не уточняющее смысла. Явная т. Строить рассуждение на тавтологии. Да это типичная т.! 2. Лог. Суждение, в котором определяемый предмет определяется… … Энциклопедический словарь
Логическая семантика — раздел логики (См. Логика), посвященный изучению значений и смыслов понятий (См. Понятие) и суждений (См. Суждение) и их формальных аналогов интерпретаций (См. Интерпретация) выражений (термов и формул) различных исчислений (См.… … Большая советская энциклопедия
ТАВТОЛОГИЯ — в обычном языке: повторение того, что уже было сказано. Напр.: «Стол есть стол». Т. бессодержательна и пуста, она не несет никакой информации, и от нее стремятся избавиться как от ненужного балласта, загромождающего речь и затрудняющего общение.… … Философская энциклопедия
ФОРМАЛЬНАЯ ЛОГИКА — наука, занимающаяся анализом структуры высказываний и доказательств, обращающая основное внимание на форму в отвлечении от содержания. Определение «формальная» было введено И. Кантом с намерением подчеркнуть ведущую особенность Ф.л. в подходе к… … Философская энциклопедия
Что значит тождественно истинно
Краткий курс логики: Искусство правильного мышления
Логика – один из обязательных предметов в высших учебных заведениях. В последнее время она также изучается в некоторых средних учебных заведениях. Практика показывает: тем, кто познакомился с логикой в школьные годы, намного легче осваивать эту науку в вузе. Книга состоит из четырёх основных глав, теста, ста занимательных задач. Первые три главы посвящены логическим формам: понятию, суждению и умозаключению, четвёртая – рассказывает о важнейших законах логики и распространённых нарушениях этих законов, которые делают наше мышление запутанным, речь – неясной, а значит, мешают полноценно общаться и понимать друг друга. Каждую тему завершают вопросы и задания для самопроверки и закрепления материала. Примеры, содержащиеся в книге, показывают практическую значимость логики для современного человека.
Тест состоит из ста заданий закрытого типа (при нескольких вариантах ответа на каждый вопрос, только один является правильным). Для выполнения теста обязательны теоретические знания по логике.
Сто занимательных логических задач, представленных в книге, различаются по типу построения и уровню сложности. Объединяет их то, что для правильного решения задач требуется нестандартный подход и творческая работа мысли. Задачи направлены на развитие мышления, памяти, внимания и воображения; они могут развлечь в часы досуга. Для решения задач не обязательны теоретические знания по логике, достаточно жизненного опыта и смекалки, т. е. интуитивной логики, которой в большей или меньшей степени обладают все люди, независимо от пола, возраста и уровня образования. Ко всем задачам приведены ответы и комментарии.
Книгу завершает список литературы, рекомендуемый для дальнейшего, более широкого изучения предмета.
Надеемся, что книга вам понравится, а изучение логики станет интересным и увлекательным.
В словаре приведены определения наиболее важных логических терминов, его можно рассматривать как конспект курса логики, построенный по алфавитно-терминологическому принципу.
Логика – наука о формах и законах правильного мышления.
Эта наука появилась приблизительно в V в. до н. э. в Древней Греции. Её создателем считается знаменитый древнегреческий философ и учёный Аристотель. Логике 2,5 тысячи лет, однако она до сих пор сохраняет своё практическое значение. Многие науки и искусства Древнего мира навсегда ушли в прошлое и представляют для нас только «музейное» значение, интересны исключительно как памятники старины, но некоторые из них пережили века, и в настоящее время мы продолжаем ими пользоваться. К их числу относится геометрия Евклида (в школе мы изучаем именно её) и логика Аристотеля. В XIX в. появилась и стала быстро развиваться символическая (математическая, современная) логика, которая является разделом высшей математики. Однако наша книга посвящена исключительно аристотелевской логике.
Так зачем нам нужна логика, какую роль она играет в нашей жизни? Логика помогает нам правильно строить свои мысли и верно их выражать, убеждать других людей и лучше понимать собеседника, объяснять и отстаивать свою точку зрения, избегать ошибок в рассуждениях.
Каждый из нас хорошо знает, что по содержанию человеческое мышление бесконечно многообразно, ведь мыслить (думать) можно о чём угодно, например, об устройстве мира и происхождении жизни на Земле, о прошлом человечества и его будущем, о прочитанных книгах и просмотренных фильмах, о сегодняшних занятиях и завтрашнем отдыхе… Но самое главное заключается в том, что наши мысли возникают и строятся по одним и тем же законам, подчиняются одним и тем же принципам, укладываются в одни и те же схемы или формы. Причём если содержание нашего мышления чрезвычайно разнообразно, то форм, в которых выражается это разнообразие, совсем немного.
Приведём простой пример. Рассмотрим три совершенно различных по содержанию высказывания: «Все караси – это рыбы», «Все треугольники – это геометрические фигуры», «Все стулья – это предметы мебели». Несмотря на различное содержание, у этих высказываний есть нечто общее, что-то их объединяющее. Что? Их объединяет форма. Отличаясь по содержанию, они сходны по форме – каждое из трёх высказываний строится по форме: «Все A – это B», где A и B – какие-либо предметы. Понятно, что само высказывание: «Все A – это B», – лишено всякого содержания. Это высказывание представляет собой чистую форму, которую можно наполнить любым содержанием, например: «Все сосны – это деревья», «Все города – это населённые пункты», «Все школы – это учебные заведения», «Все тигры – это хищники».
Другой пример: возьмём три различных по содержанию высказывания: «Если наступает осень, то опадают листья», «Если завтра пройдёт дождь, то на улице будут лужи», «Если вещество – металл, то оно электропроводно». Будучи непохожими друг на друга по содержанию, эти высказывания сходны между собой тем, что строятся по одной и той же форме: «Если A, то B». Понятно, что к этой форме можно подобрать огромное количество различных содержательных высказываний, например: «Если не подготовиться к контрольной работе, то можно получить двойку», «Если взлётная полоса покрыта льдом, то самолёты не могут взлетать», «Если слово стоит в начале предложения, то его надо писать с большой буквы».
Логика не интересуется содержанием мышления (им занимаются другие науки), она изучает только формы мышления; её интересует не то, что мы мыслим, а то, как мы мыслим, поэтому она часто называется формальной логикой. Аристотелевскую (формальную) логику также часто называют традиционной.
Если по содержанию высказывание: «Все комары – это насекомые», – является нормальным, а высказывание: «Все Чебурашки – это инопланетяне», – абсурдным, то для логики эти два высказывания равноценны, так как она занимается формами мышления, а форма у этих высказываний одна и та же: «Все A – это B».
Форма мышления – это способ выражения мыслей, или схема их построения.
Существует всего три формы мышления:
1. Понятие – это форма мышления, которая обозначает какой-либо объект или признак объекта. Примеры понятий: карандаш, растение, небесное тело, химический элемент, мужество, глупость, нерадивость.
2. Суждение – это форма мышления, которая состоит из понятий, связанных между собой, и что-либо утверждает или отрицает. Примеры суждений: «Все планеты являются небесными телами», «Некоторые школьники – это двоечники», «Все треугольники не являются квадратами».
3. Умозаключение – это форма мышления, в которой из двух или нескольких исходных суждений (посылок) вытекает новое суждение (вывод).
В логике принято располагать посылки и вывод друг под другом и отделять посылки от вывода чертой.