Что значит точка внутри угла

Что значит точка внутри угла

Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.

Лучи называются сторонами угла, а их общее начало − вершиной угла.

Обозначение угла

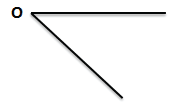
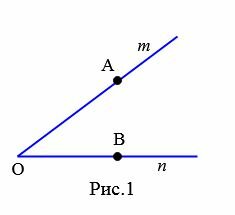
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают \( \small ∠mn \) или \( \small ∠O. \) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: \( \small ∠AOB \) или \( \small ∠BOA. \)

Развернутый угол. Внутренняя и внешняя область угла

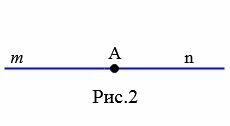
Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.

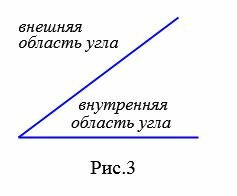
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).

Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.

Фигуру, состоящую из угла и его внутренней области также называют углом.

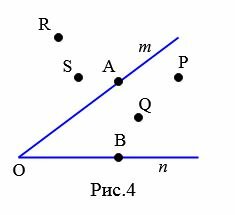
На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.

Типы углов

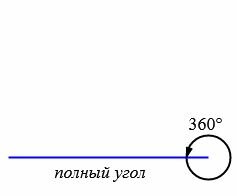
В зависимости от величин, углы бывают следующих типов (Рис.5):

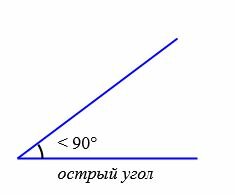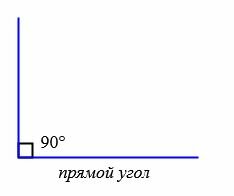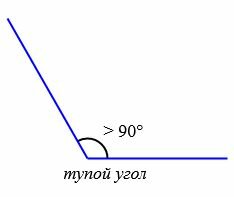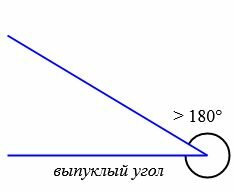Сравнение углов

Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.

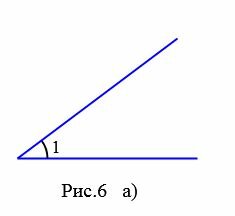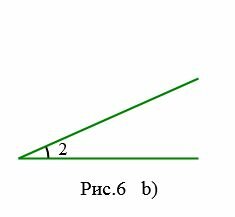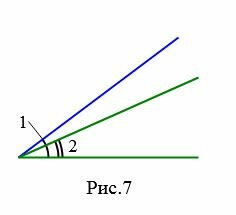
На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: \( \small ∠2 \lt \angle 1. \)

Градусная мера угла

Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является \( \small \frac <1> <180>\) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).

Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: \( \small ∠AOB=120 °. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \small \frac <1> <60>\) часть градуса называется минутой и обозначается так: » ‘ «. \( \small \frac <1> <60>\) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: \( \small \angle AOB=56°6’43». \)

Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.

Источник

Что значит точка внутри угла

Мы знаем, что углом называется геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

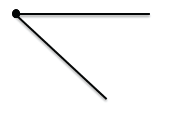
Изображать угол можно и так (не отмечаем точкой общее начало, считаем, что точка есть)

Обозначения угла

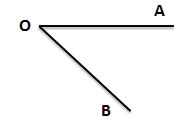
На сторонах угла не отмечены точки (только обозначены большими латинскими буквами А и В)

Считается, что буква А обозначает любую точку на верхней стороне угла (по данному рисунку)

Точка В обозначает любую точку на нижней стороне угла (по данному рисунку)

Читаем: угол АОВ

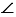
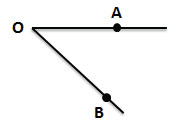
Пишем: АОВ

На сторонах угла отмечены и обозначены произвольные точки А и В

Читаем: угол АОВ

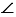
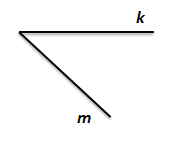
Пишем: АОВ

Стороны угла (лучи) обозначены малыми латинскими буквами k и m

Читаем: угол km

Пишем: 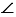km

Обозначена только вершина угла

Читаем: угол О

Пишем: 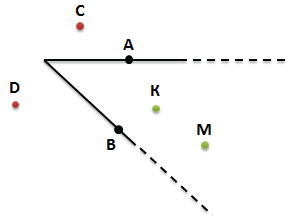О

Развернутый угол

Построим прямую АВ и отметим на этой прямой точку О

Лучи ОА и ОВ лежат на одной прямой (являются дополнительными)

Угол АОВ называется развернутым

Угол на плоскости

Изобразим часть плоскости

(так как плоскость бесконечна, мы не можем изобразить ее всю, только часть ее)

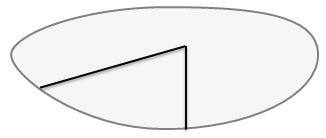
Построим на этой плоскости неразвернутый угол

Замечание

Любой угол разделяет плоскость на две ча­сти. Названия этих частей ( внутренняя область и внешняя область) применяется для неразвернутого угла.

Если угол развёрнутый, то любую из двух частей, на которые он разделяет плоскость, мож­но считать внутренней областью угла.

Расположение точек относительно угла

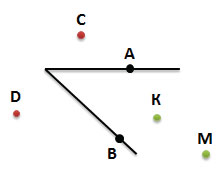
По рисунку определим положение отмеченных точек A, B, C, D, K, M

Точки А и В лежат на сторонах угла

Точки D и C лежат вне угла (во внешней об­ласти угла)

Точки К и М, лежат внутри угла (во внутренней об­ласти угла)

При необходимости мы можем продолжить стороны угла, например, чтобы уточнить положение точки М

Поделись с друзьями в социальных сетях:

Источник

Математика.Точка лежит внутри угла

30 Mar 2020 в 19:33

30 Mar 2020 в 19:33 #1

Она прикасается к прямым образующим этот угол?Или нет?

30 Mar 2020 в 19:34 #2

Ну значит внутри треугольного объекта

30 Mar 2020 в 19:34 #3

Нужно задание видеть, а так скорей всего имеется ввиду вершина угла

30 Mar 2020 в 19:36 #4

Нужно задание видеть, а так скорей всего имеется ввиду вершина угла

30 Mar 2020 в 19:40 #5

При такой формулировке подойдут любые положения между ОА и ОB, не касающиеся OA, OB и OC

30 Mar 2020 в 19:40 #6

При такой формулировке подойдут любые положения между ОА и ОB, не касающиеся OA, OB и OC

То есть кароче в пространстве между палками.

30 Mar 2020 в 19:41 #7

Эта плоскость ограничена двумя лучами, выходящими из вершины угла. Точка, лежащая внутри угла, лежит внутри данной плоскости.

30 Mar 2020 в 19:44 #8

30 Mar 2020 в 19:45 #9

А m то где находится.

Ну я уже понял что в плоскости ограниченной двумя лучами.

30 Mar 2020 в 20:16 #10

А m то где находится.

Ну я уже понял что в плоскости ограниченной двумя лучами.

Не касается 3х линий и между ними, в произвольном порядке можешь расположить

30 Mar 2020 в 20:21 #11

Она прикасается к прямым образующим этот угол?Или нет?

Источник

Свойство точек биссектрисы угла:

По определению биссектриса угла делит угол пополам.

У биссектрисы есть еще одно важное свойство.

Теорема (о биссектрисе угла).

Любая точка биссектрисы угла равноудалена от сторон угла. Если точка внутри угла равноудалена от сторон угла, то она лежит на биссектрисе этого угла.

В данной теореме два утверждения: прямое и ему обратное. Докажем каждое из этих утверждений отдельно.

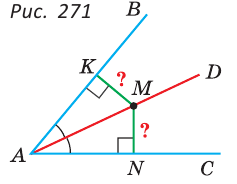
1) Дано: AD — биссектриса

Доказательство:

Прямоугольные треугольники АКМ и ANM равны по гипотенузе и острому углу (гипотенуза AM — общая, KAM =NAM, так как AD — биссектриса). Катеты МК и MN равны как соответствующие в двух равных треугольниках.

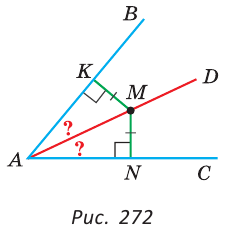
2) Дано: BAC, МКAB, MNAC, МК = MN, MAD (рис. 272).

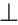
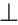
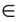
Доказать: луч AD — биссектриса 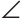BAC.

Доказательство:

Прямоугольные треугольники АКМ и ANM равны по катету и гипотенузе (гипотенуза AM — общая, МК = MN по условию). Углы КAM и NAM равны как соответствующие в двух равных треугольниках, откуда луч AD — биссектриса 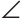BAC. Теорема доказана.

Из доказанной теоремы следует, что биссектриса является геометрическим местом точек плоскости, находящихся внутри угла и равноудаленных от сторон угла.

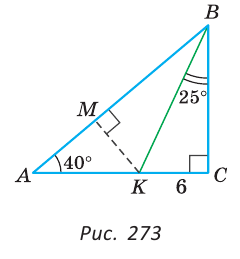
Пример:

В прямоугольном треугольнике ABC C = 90°, A = 40° (рис. 273). На катете АС взята точка К так, что КС=6 см и KBC = 25°. Найти расстояние от точки К до прямой АВ.

Решение:

Пример: (2-я замечательная точка треугольника).

Доказать, что биссектрисы треугольника пересекаются в одной точке.

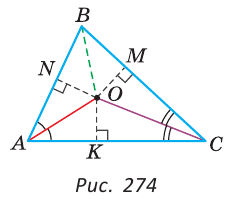
Доказательство:

Проведем в АВС биссектрисы углов А и С. Пусть О — точка их пересечения (рис. 274).

Так как точка О лежит на биссектрисе АО угла А, то она равноудалена от сторон угла А, то есть равны перпендикуляры ON и ОК к сторонам угла А. Так как точка О лежит на биссектрисе СО угла С, она равноудалена от сторон угла С, то есть равны перпендикуляры ОК и ОМ к сторонам угла С. Тогда ОК = ОМ = ON. Так как перпендикуляры ON и ОМ равны, то точка О равноудалена от сторон угла В. Точка, равноудаленная от сторон угла, лежит на биссектрисе этого угла. Поэтому биссектриса угла В пройдет через точку О, и, следовательно, все три биссектрисы пересекутся в одной точке.

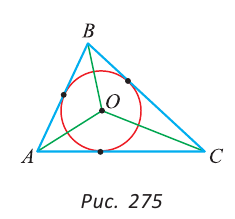
Замечание. Точка пересечения биссектрис треугольника является центром вписанной в него окружности (рис. 275), которая касается всех трех сторон треугольника (имеет с каждой из сторон только одну общую точку).

Пример:

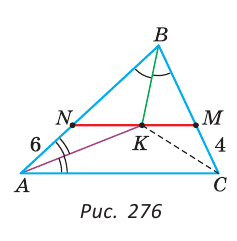
В треугольнике ABC биссектрисы углов А и В пересекаются в точке К. Через точку К проведен отрезок NM, параллельный стороне АС с концами на сторонах АВ и ВС соответственно; AN = 6 см, МС = 4 см. Найти отрезок NM.

Решение:

Так как биссектрисы треугольника пересекаются в одной точке, то СК — биссектриса угла С (рис. 276).

Треугольник ANK — равнобедренный. Действительно, NAK =CAK, поскольку АК — биссектриса, CAK =AKN как накрест лежащие при параллельных прямых NM и АС и секущей АК, откуда NAK =AKN и треугольник ANК — равнобедренный по признаку равнобедренного треугольника. Тогда NK=AN=6 см. Аналогично доказываем, что треугольник KMC — равнобедренный и КМ=МС=4 см.

Искомый отрезок NM = NK + КМ = 6 + 4=10 (см).

Замечание. Решив задачу 3, мы доказали, что если NM || АС и отрезок NM проходит через точку пересечения биссектрис, то периметр NBM равен АВ+ВС.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Что значит точка внутри угла

Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, то есть два луча с общим началом называются углом. Лучи, образующие угол, называются сторонами угла, а их общее начало — вершиной угла.

Обозначение углов

Угол обозначается или одной буквой или цифрой, поставленной при вершине угла, например угол A или угол 1, или тремя буквами, из которых одна стоит при его вершине, а две другие при каких-либо точках его сторон. При обозначении угла тремя буквами, буква, стоящая при его вершине, произносится и пишется между двумя другими, например угол AOB. Слово угол в записи заменяют знаком ∠, например ∠1.

Внутренняя и внешняя область

Два луча, исходящие из одной точки, образуют два угла. Для обозначения нужного угла, угол обычно помечается дугой:

Если рассматриваются оба угла, образованные двумя лучами, то они помечаются разным числом дуг, но только в том случае, если углы не равны. Равные углы обозначаются одинаково.

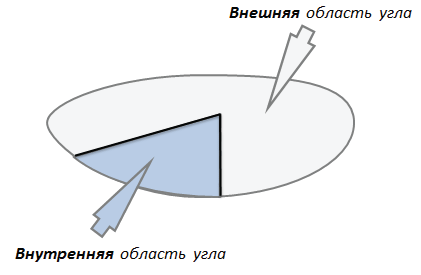
Любой угол делит плоскость на две области. Одна область обычно называется внутренней, а другая внешней. Внутренняя область угла — это часть плоскости, расположенная между сторонами рассматриваемого угла:

Внешняя область угла — это часть плоскости, которая не принадлежит рассматриваемому углу.

Источник