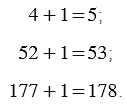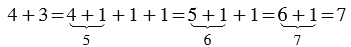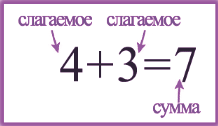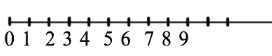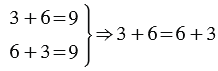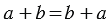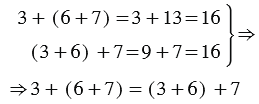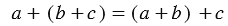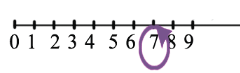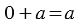Что значит свойства сложения при вычислении суммы
Сложение натуральных чисел. Свойства сложения
При таом поразрядном сложении вычисления приходится проводить только с однозначными числами, что не вызывает затруднений.
Напомним, что в равенстве a + b = c числа a и b называют слагаемыми, число с и запись a + b − суммой. Здесь буквами обозначены числа.
Вам хорошо известно переместительное свойство сложения.
От перестановки слагаемых сумма не меняется.
В буквенном виде это свойство записывают так:
a + b = b + a
Скорее всего вы поступите так:
Здесь мы воспользовались сочетательным свойством сложения.
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.
В буквенном виде это свойство записываю так:
(a + b) + c = a + (b + c)
Из свойств сложения следует, что при сложении нескольких чисел слагаемые можно менять местами и заключать их в скобки, тем самым определяя порядок вычислений.
Например, верны равенства:
2 + 3 + 7 + 8 = ( 2 + 8 ) + ( 7 + 3 ).
При сложении число 0 обладает особым свойством: если одно из двух слагаемых равно нулю, то сумма равна другому слагаемому:
a + 0 = a,
0 + a = a.
Используя переместительно и сочетательное свойства сложения, получаем:
136 + (a + 214 ) = 136 + ( 214 + a) = ( 136 + 214 ) + a = 350 + a.
Учитывая, что 1 мин = 60 с, имеем:
7 мин 44 с + 5 мин 38 с = 7 мин + 44 с + 5 мин + 38 с = ( 7 мин + 5 мин) + ( 44 с + 38 с) = 12 мин + 82 с = 12 мин + 60 с + 22 с = 12 мин + 1 мин + 22 с = 13 мин 22 с.
Сложение натуральных чисел
К нескольким натуральным числам прибавим 1:
Мы видим, что когда мы прибавляем к натуральному числу 1, получаем следующее за ним натуральное число, т.е. следующее число больше предыдущего на единицу. Теперь к 4 прибавим 3: 4+3: для этого к 4 прибавим 3 раза единицу. Учитывая, что при прибавлении к числу единицы получаем следующее число, получим:
Но мы записываем коротко: 4+3=7.
Числа, которые складываются, называются слагаемыми, число, которое получается в результате сложения, называется суммой.
Сложение чисел на координатном луче
Изобразим координатный луч. Отметим на нем начало координат, единичный отрезок и несколько чисел, следующих друг за другом:
Рассмотрим наш пример: 4+3. Для того чтобы к 4 прибавить 3 на координатном луче, необходимо от точки 4 вправо отложить 3 единичных отрезка:
И мы попадем в точку 7, следовательно 4+3=7.
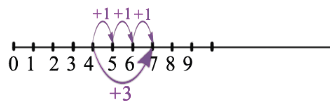
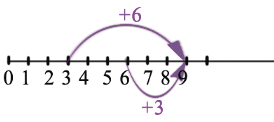
Теперь попробуем отложить на луче, от точки 3 6 единичных отрезков, и от точки 6 3 единичных отрезка, другими словами к 3 прибавим 6 и к 6 прибавим 3 :
Мы видим, что и в первом и во втором случае мы попадаем в одну и ту же точку: 9, следовательно сумма чисел 3 и 6 и 6 и 3 одинакова и равна 9. Это можно записать с помощью равенства:
В этом случае мы меняем местами слагаемые и получаем первое свойство сложения — переместительное свойство :
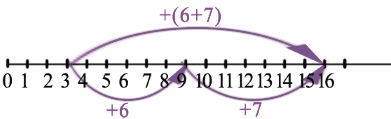
Рассмотрим с помощью координатного луча следующие суммы: 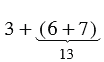
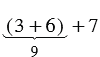
Заметим, что и в первом и во втором случае мы попадаем в одну точку: 16. Это можно записать равенством:
К натуральному числу можно прибавлять не только натуральное число, но еще и нуль, изобразим на луче прибавление нуля к 7:
Свойства сложения
От перестановки слагаемых сумма не меняется
Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое
Если прибавить к нулю какое-нибудь число, то получится прибавленное число
Сравнение сумм натуральных чисел
Сравним (15+81) и (15+77), для этого рассмотрим слагаемые этих двух сумм: Мы видим, что первые слагаемые у них одинаковые, поэтому переходим к сравнению вторых слагаемых: 81 >77, поэтому (15+81)>(15+77).
Теперь сравним (21+15) и (34+54), для этого опять рассмотрим слагаемые, в данном случае одинаковых у нас нет, но мы видим, что слагаемые первой суммы меньше слагаемых второй суммы, а значит мы можем записать: (21+15) При увеличении слагаемых сумма увеличивается, а при уменьшении уменьшается.
Письменный прием сложения («сложение в столбик»)
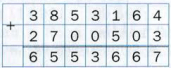
Часто при решении задач, нам необходимо складывать многозначные числа, поэтому считать в «уме» или чертить координатный луч не целесообразно, для решения таких задач был придуман письменный прием сложения или «сложение в столбик», который помогает сложение многозначных чисел свести к сложению однозначных чисел, которое мы можем производить легко. Рассмотрим пример:
| 1 | 1 | 1 | |||
| + | 4 | 5 | 8 | 7 | 1 |
| 4 | 3 | 8 | 2 | ||
| 5 | 0 | 2 | 5 | 3 |
Вывод: Если при сложении чисел одного разряда число получается больше или равное 10, то 1 десяток записываем над следующим разрядом, а единицы под рассматриваемым разрядом.
Поделись с друзьями в социальных сетях:
Свойства сложения
Содержание
Мы уже умеем складывать числа с помощью рисунка и координатного луча. Умеем складывать однозначные числа, такие как 7 и 5, и многозначные, такие как 123 и 456.
Для того чтобы складывать числа было легче, существует несколько простых правил. Их еще называют законами сложения или свойствами.
Закон – это что-то, что никогда не меняется, и что можно применять для всех чисел.
Заучивать законы сложения не нужно, их нужно только один раз понять и научиться использовать в примерах и задачах. Сделать это очень просто. Сейчас мы сможем в этом убедиться.
Переместительное свойство
Первый закон сложения называется переместительным законом сложения. Звучит он так:
От перестановки слагаемых сумма не меняется.
Чтобы понять этот закон, мы решим один и тот же пример двумя способами.
А теперь поменяем наши числа местами и посчитаем ответ:
Результаты сложения получились одинаковыми. Но заметим, что во втором случае посчитать было гораздо проще, не так ли? Значит, проще было поменять числа местами и потом посчитать.
Сложение с нулем
В корзине было 100 яблок, туда положили 0 яблок, сколько яблок стало в корзине?
Очевидно, что если в корзину не положили яблок, то количество яблок в ней не изменилось, то есть по-прежнему равно 100.
От прибавления нуля число не изменяется
$10+0 = 10$
$0 + 8 = 8$
$0 + 0 = 0$
Сочетательное свойство
В некоторых примерах бывает нужно сложить не два числа, а несколько.
Складываем все числа слева направо привычным для нас способом. Получаем:
Если мы внимательно посмотрим на числа, то сможем увидеть, что легче сначала сложить 4 и 6, а затем к полученной сумме прибавить и число 29.
$29 + 4 + 6 = 24 + 10 = 39$
Ответ получился таким же.
Значит, при сложении нескольких чисел можно складывать сначала те числа, которые нам удобнее сложить. А затем уже к полученной сумме прибавляем оставшиеся числа. Мы, так сказать, сочетаем те числа, которые легче посчитать при сложении.
Этот закон называется сочетательный закон сложения. Кратко он звучит так:
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.
Законы сложения можно применять при сложении не только двух или трех, но и большего количество чисел.
Чтобы решить этот пример, посмотрим внимательно на числа. Заметим, что легче всего было бы сложить 128 и 12, а к числу 383 легче прибавить 17. Поэтому мы сейчас поменяем местами числа 17 и 12. То есть применим в нашем примере переместительный закон. Получим:
Теперь группируем попарно числа, которые будем складывать. То есть применим сочетательный закон. Для этого мы используем скобки:
Считаем, сколько получится в скобках и складываем результаты:
Вот так легко и быстро мы получили ответ, применяя законы сложения.
Вычитание натуральных чисел
Пройти тест по теме «Сложение и вычитание натуральных чисел» можно по ссылке. Проверьте свои знания!
Мы можем не только собирать в группы различные предметы, то есть, складывать их, но и забирать из существующей группы определенное их количество.
Разность (или остаток) – это такое число, которое получится, если от одного числа отнять другое, то есть, от всех единиц одного числа отнять все единицы, которые содержатся в другом числе.
Уменьшаемое – это то число, от которого мы отнимаем единицы другого числа.
Вычитаемое – это число, которое мы вычитаем из другого числа. То есть, то число, на количество единиц которого мы уменьшаем другое число.
Вычитание – это арифметическое действие, которое выполняется для получения разности двух или нескольких чисел.
то есть, совершить действие вычитания – это найти такое число, которое получится, если от данного числа отнять определенное количество единиц другого числа.
Совершая вычитание натуральных чисел, вы должны помнить, что из одного натурального числа можно вычесть только равное ему или меньшее натуральное число. Действительно, мы никак не можем отобрать единиц предметов больше, чем их есть в наличии.
Связь вычитания и сложения
Действительно, когда мы ищем сумму, мы складываем все единицы, из которых состоят числа, вместе. То есть, получаем число, которое складывается из разных чисел.
Поэтому, вычитание и сложение – это взаимно обратные действия. Если нам известна сумма двух слагаемых, мы можем превратить ее в разность двух чисел, и наоборот, разность можно перевести в сумму.
Свойства разности натуральных чисел
Свойства разности натуральных чисел состоят из:
Рассмотрим каждый пункт подробнее.
Правила вычитания суммы из числа и числа из суммы
Как вычесть сумму из числа
Чтобы найти разность числа и суммы чисел нужно из данного числа вычесть последовательно каждое слагаемое суммы.
То есть, сначала мы находим разность между данным числом и первым слагаемым, потом от этой полученной разности отнимаем второе слагаемое, третье, и так далее до последнего слагаемого суммы.
Рассмотрим это на примере из урока сложение чисел.
325 +( 12 + 64 + 5 ) = 325 +81 = 406
Я запишу это в виде разности:
и покажу, что результат будет равен первому слагаемому:
Как видите, все верно.
Как вычесть число из суммы
Чтобы найти разность суммы чисел и некоторого числа, нужно отнять это число от какого-нибудь подходящего слагаемого этой суммы.
То есть, мы сначала находим разность одного из слагаемых и данного числа, а потом складываем получившийся результат последовательно с остальными слагаемыми.
Действительно, вы знаете, что, если уменьшить одно из слагаемых на какое-то число, то и сумма уменьшится на это же самое число. Следовательно, если нам нужно сумму чисел уменьшить на какое-то число, то для этого достаточно уменьшить на это число одно из слагаемых суммы.
Для рассмотрения я возьму тот же пример, только сумму расчленю на слагаемые, а слагаемое в скобках заменю суммой:
325 +81 = ( 191 + 65 + 150 )
Превращаю выражение в разность:
( 191 + 65 + 150 )-81 = 325
и покажу, что результат также будет равен первому слагаемому:
Как меняется разность при изменении вычитаемого или уменьшаемого
Изменение разности при изменении вычитаемого и уменьшаемого является следствием описанных в уроке изменений суммы чисел с изменением ее слагаемых.
Если уменьшаемое увеличить на некоторое количество единиц, то и разность увеличится на такое же количество единиц.
Если уменьшаемое уменьшить на некоторое количество единиц, то и разность уменьшится на такое же количество единиц.
Если вычитаемое увеличить на некоторое количество единиц, то разность уменьшится на такое же количество единиц.
Если вычитаемое уменьшить на некоторое количество единиц, то разность увеличится на такое же количество единиц.
Если сразу оба числа, и уменьшаемое, и вычитаемое, увеличить или уменьшить на одно и то же количество единиц, то разность не изменится.
Правила вычитания разности
Если нужно вычесть из числа разность других чисел, можно воспользоваться одним из двух способов:
1. Прибавить к данному числу вычитаемое, и из получившейся суммы вычесть уменьшаемое;
2. Вычесть из данного числа уменьшаемое, а потом результат этого действия сложить с вычитаемым.
Это свойство выводится из предыдущих, рассмотренных нами.
22 — 17 = 5
5+ 3 = 8
22 +3-( 17 +3- 3 )
25- 17 +0 = 8
Как видите, оба способа показали верный результат.
Вычитание однозначного числа
Вычитание в столбик многозначных чисел
Вычитание в столбик – это способ нахождения разности чисел при помощи их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим), и последующего вычисления.
После нахождения разности чисел способом вычитания в столбик записываем ответ в строчном примере:
50063-4825 = 45238.
Как проверить действия сложение и вычитание?
Проверить сложение можно двумя способами: обратным сложением и вычитанием.
Обратное сложение означает, что мы меняем слагаемые местами, и складываем их еще раз. Если результат будет такой же, как и после первого сложения, значит, вычисление было верным.
Проверка сложения вычитанием – это способ, при котором нужно из суммы, которую получили после выполнения действия сложение, отнять одно из слагаемых. Если результат этого вычитания будет равен второму слагаемому (или сумме остальных слагаемых, если их больше двух), значит сложение было выполнено верно.
И этот способ проверки показал правильность нашего решения.
Проверить вычитание также возможно и сложением, и другим вычитанием.
Проверка вычитания сложением основана на взаимосвязи вычитания и сложения. Зная, что уменьшаемое – это сумма, а остаток и вычитаемое – это слагаемые, мы можем сложить между собой вычитаемое и остаток, и, если получим в результате уменьшаемое, значит, мы правильно сделали действие.
Вот так выглядит проверка вычитания сложением на примере вычисленной на этом уроке разницы 50063-4825 = 45238 :
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
Здравствуйте! Начнем урок с загадок.
Очень любит сладкий мед.
Озорник он и проказник,
Не всегда ему везет.
Ребята, вы догадались, о ком идет речь? Конечно, о Винни – Пухе!
Медвежонку лучший друг –
Это знают все вокруг!
Не бычок, и не волчок,
Да, веселый Пятачок!
Сегодня Винни – Пух и Пятачок будут учиться вместе с нами. Они приготовили для урока тетради в клеточку, вооружились цветными ручками, фломастерами и карандашами. Ну что ж, за дело!
Устные вычисления в пределах 100
Разложите числа: 69, 56, 66, 31, 77 на разрядные слагаемые.
Решим вместе такие примеры:
Переместительное и сочетательное свойства сложения
Ребята, запомним свойства сложения! С их помощью вычислять получается гораздо быстрее и легче.
Эти свойства показывают, что мы можем переставлять слагаемые, как удобно, а значит, позволяют упрощать вычисления.
7 + 9 + 3 + 1 + 8 + 6 + 2 + 4 + 3
Будем использовать оба свойства. Можно складывать в любом порядке.
Посмотрите внимательно на примеры! Какие два числа в сумме дают круглое число? Соединим их дугой. Внизу под дугой подпишем результат.
Решите самостоятельно примеры. Соединяйте дугой слагаемые (так удобнее и быстрее):
Есть другой способ записи: с использованием скобок.
Решим еще несколько примеров. Вычислим устно удобным способом следующие суммы:
20 + 8 + 40 + 2 = (20 + 40) + (8 + 2) = 60 + 10 = 70
30 + 1 + 9 + 60 = (30 + 60) + (1 + 9) = 90 + 10 = 100
Задачи на нахождение неизвестного слагаемого
Ребята, помогите Пятачку и Винни – Пуху найти вторую половинку правила:
Это правило пригодится нам, чтобы верно решить задачу.
Посмотрите, Пятачок и Винни – Пух идут друг к другу в гости. Дорожка длиной 80 м. Пятачок прошел до встречи 30 м. Сколько метров прошел до встречи Винни – Пух?
Схема нам поможет понять задачу.
Сколько прошел Пятачок? 30 м.
А сколько прошел Винни – Пух? Не знаем.
Из чего состоит длина дорожки? Из расстояния, которое прошли Пятачок и Винни – Пух вместе.
С1 + С2 = С
Что неизвестно? Второе слагаемое.
Как его найти? С2 = С – С1
Решение: 80 – 30 = 50 (м) – прошел до встречи Винни – Пух.
Математика вокруг нас
Мы с вами даже не подозреваем о том, что математика – всюду! Давайте вместе с Пятачком и Винни – Пухом отправимся в гости к Кролику и попробуем отыскать математику в самых простых привычных вещах. Понаблюдаем за формой, цветом, размером предметов.
Вот мы с вами у дома Кролика.
Ребята, скажите, какой формы клумбы в цветнике?
Верно, мы с вами видим четырехугольники и круг. Посмотрите, как здорово Кролик подобрал цветы для своей клумбы: здесь и белые ромашки, и желтые бархатцы, и красные гвоздики. Ярко и празднично.
А это маленький огород Кролика. Какие геометрические фигуры вы увидели? Какого они размера?
Кролик пригласил своих гостей на чаепитие. Какие геометрические фигуры вы видите в орнаменте и узорах на тарелках и чашках?
Верно, мы видим круги, многоугольники, волнистые и ломаные линии, овалы и точки.
Винни – Пух и Пятачок испекли пирог для чаепития. Он получился вкусным, потому что все было сделано по рецепту.
Вот видите, ребята, и здесь пригодилась математика!
Ну что ж, пора нашим героям отправляться в лесную школу. Их там уже давно ждут.
Посмотрите на часы, которые висят на стене. Определить, который час, нам поможет математика. Маленькая часовая стрелка показывает на число 10, а большая минутная стрелка – на 12 (здесь она начинает свой отсчет). Значит, сейчас ровно 10 часов 00 минут.
Задачи повышенной сложности
Ребята, поможем нашим героям справиться с задачами повышенной сложности. Научим их и научимся сами рассуждать, логически мыслить.
В лесной школе прошла математическая олимпиада. В финал олимпиады вышли две белки и два зайца. Все вместе они решили 11 задач: каждый – разное количество. Кто решил больше задач: зайцы или белки, если один заяц решил задач больше всех, а другой заяц – меньше всех.
Для решения этой задачи надо подбирать разные числа и проверять, подходят ли они.
Для удобства начертим таблицу.
Нужно в сумме набрать 11 так, чтобы все слагаемые были разные. Пусть первый заяц решит всего 1 задачу (меньше всех). Белки решат разное количество, например, 2 и 3. Ну а второй заяц решит больше всех – это 5.
1 + 2 + 3 + 5 = 11. В сумме получилось 11 задач.
Значит, зайцы решили: 1 + 5 = 6, белки решили: 2 + 3 = 5.
Ответ: зайцы решили задач больше, чем белки.
Сегодня в лесной школе все с увлечением мастерили фигурки в технике оригами.
Давайте рассуждать вместе! Чертим таблицу.
Поставим знак « – »в ячейке напротив героев сказки. Мы знаем, что у Пятачка – не кораблик и не лиса. У него – птичка, значит, у Кролика птички нет, и ему остается кораблик. А у Винни – Пуха – фигурка лисы.
Молодцы, ребята! Приходите еще, порешаем вместе! А теперь проверьте свои знания. Всем пока!
В материалах урока использованы кадры из м/с «Винни-Пух»