Что значит среднее значение
Простая формула, чтобы подсчитать среднее арифметическое
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
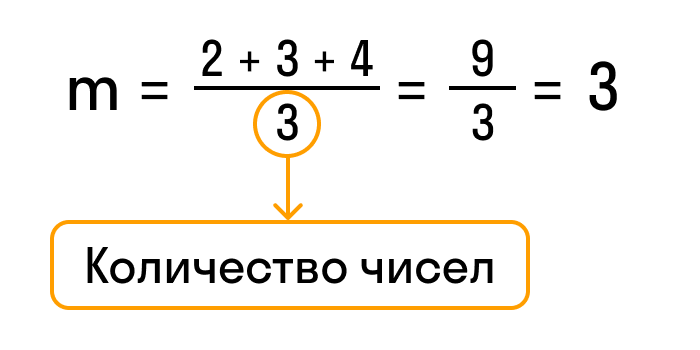
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
Среднее арифметическое: физический смысл и визуализация
Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:
Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.
Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.
Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.
Среднее арифметическое двух чисел
Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:
Их среднее арифметическое:
Физический смысл среднего арифметического
Изобразим два исходных числа и их среднее арифметическое на числовой оси:
Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.
В механике момент силы – это произведение силы F на расстояние l:
На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l1 и l2, получим:
Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:
Обозначив m координату точки опоры весов, получим:
Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:
Координата опоры весов m:
Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.
Визуальное восприятие равновесия
Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.
Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:
На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.
Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:
Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.
Математическое ожидание случайной величины
Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:
Теперь точка опоры весов в равновесии это μ:
Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:
Это и есть формула математического ожидания.
Гистограмма
Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.
На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.
Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:
Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:
Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:
Дайте мне точку опоры, и я переверну Землю. Архимед
Как правильно вычислить среднее значение?
Средняя зарплата… Средняя продолжительность жизни… Практически каждый день мы с вами слышим эти словосочетания, используемые для описания множества одним единственным числом. Но как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека.
В чем проблема?
Под средним значением чаще всего подразумевается среднее арифметическое, которое очень сильно варьируется под воздействием единичных фактов или событий. И вы не получите реального представления о том, как именно распределены значения, которые вы изучаете.
Давайте обратимся к классическому примеру со средней зарплатой.
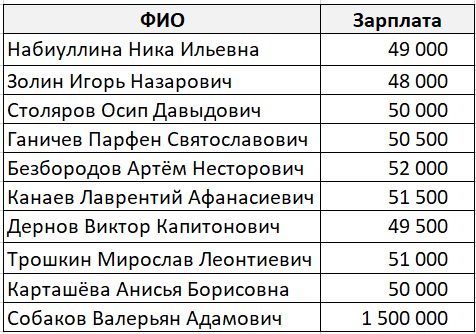
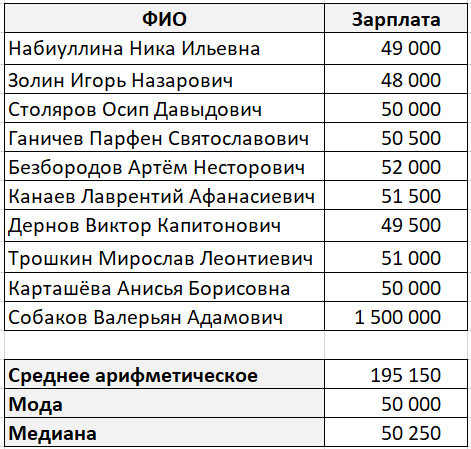
В какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).
Средним значением в данном случае будет 195 150 рублей, что согласитесь, неправильно.
Какие способы вычисления среднего бывают?
Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.
Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.
Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.
Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).
А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:
И вот какие значения у нас получились:
В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.
Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.
Вычисляем среднее арифметическое на SQL
И чтобы ее использовать достаточно написать вот такой запрос:
Вычисляем моду на SQL
В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.
Вычисляем медиану на SQL
Выглядит все это так:
Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.
Какой способ все-таки использовать?
Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.
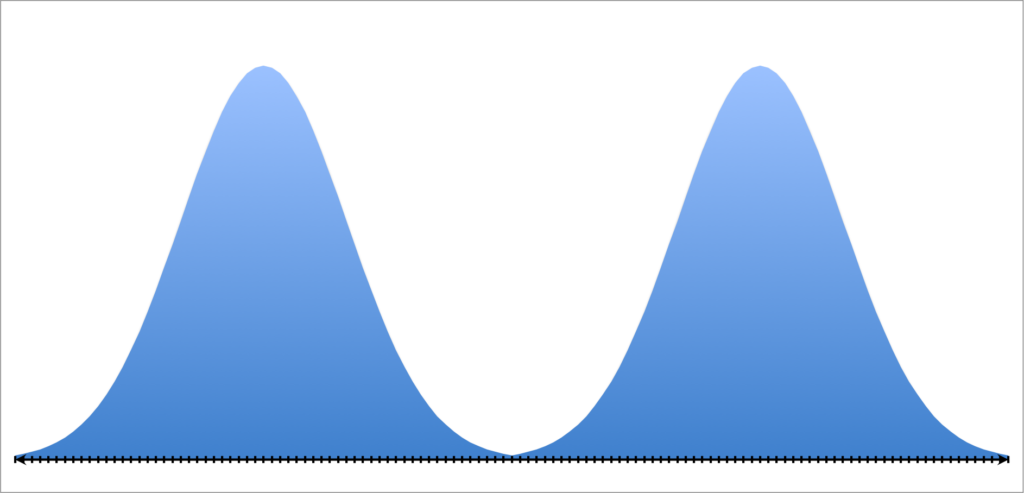
Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:
На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при голосовании на выборах.
В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.
А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.
Вывод:
При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.
Окончательный выбор меры центральной тенденции всегда лежит на аналитике.
Средние величины и показатели вариации
Понятие и виды средних величин
Существует 2 класса средних величин: степенные и структурные.
К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.
Степенные средние величины
Степенные средние могут быть простыми и взвешенными.
Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:
Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида, которые будут далее подробно рассмотрены.
Средняя арифметическая
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической простой: (3+4+4+5)/4 = 16/4 = 4.
Средняя арифметическая взвешенная имеет следующий вид:
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической взвешенной: (3*1 + 4*2 + 5*1)/4 = 16/4 = 4.
Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X отсутствует нижняя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.
Средняя арифметическая применяется чаще всего, но бывают случаи, когда необходимо применение других видов средних величин. Рассмотрим такие случаи далее.
Средняя гармоническая
Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:
Средняя геометрическая
Средняя геометрическая применяется при определении средних относительных изменений, о чем сказано в теме Ряды динамики. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.
Средняя квадратическая
Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.
Главной сферой применения квадратической средней является измерение вариации значений X, о чем пойдет речь позднее в этой лекции.
Средняя кубическая
Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.
Структурные средние величины
К наиболее часто используемым структурным средним относятся статистическая мода и статистическая медиана.
Статистическая мода
Если X задан дискретно, то мода определяется без вычисления как значение признака с наибольшей частотой. В статистической совокупности бывает 2 и более моды, тогда она считается бимодальной (если моды две) или мультимодальной (если мод более двух), и это свидетельствует о неоднородности совокупности.
Если X задан равными интервалами, то сначала определяется модальный интервал как интервал с наибольшей частотой f. Внутри этого интервала находят условное значение моды по формуле:
где Мо – мода;
ХНМо – нижняя граница модального интервала;
hМо – размах модального интервала (разность между его верхней и нижней границей);
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующего модальному;
fМо+1 – частота интервала, следующего за модальным.
Если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.
Статистическая медиана
Если X задан дискретно, то для определения медианы все значения нумеруются от 0 до N в порядке возрастания, тогда медиана при четном числе N будет лежать посередине между X c номерами 0,5N и (0,5N+1), а при нечетном числе N будет соответствовать значению X с номером 0,5(N+1).
Если X задан в виде равных интервалов, то сначала определяется медианный интервал (интервал, в котором заканчивается одна половина частот f и начинается другая половина), в котором находят условное значение медианы по формуле:
где Ме – медиана;
ХНМе – нижняя граница медианного интервала;
hМе – размах медианного интервала (разность между его верхней и нижней границей);
fМе – частота медианного интервала; 
Также как и в случае с модой, при определении медианы если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.
Показатели вариации
Размах вариации
Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:
Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.
Cреднее линейное отклонение
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4. Рассчитаем среднее линейное отклонение простое: Л = (|3-4|+|4-4|+|4-4|+|5-4|)/4 = 0,5.
Вернемся к примеру про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4 и среднее линейное отклонение простое = 0,5. Рассчитаем среднее линейное отклонение взвешенное: Л = (|3-4|*1+|4-4|*2+|5-4|*1)/4 = 0,5.
Линейный коэффициент вариации
С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.
В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, линейный коэффициент вариации составит 0,5/4 = 0,125 или 12,5%.
Дисперсия
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил оценки: 3, 4, 4 и 5, ранее уже была рассчитана средняя арифметическая = 4. Тогда дисперсия простая Д = ((3-4) 2 +(4-4) 2 +(4-4) 2 +(5-4) 2 )/4 = 0,5.
В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию взвешенную: Д = ((3-4) 2 *1+(4-4) 2 *2+(5-4) 2 *1)/4 = 0,5.
Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию методом разности средней квадратов и квадрата средней:
Д = (3 2 *1+4 2 *2+5 2 *1)/4-4 2 = 16,5-16 = 0,5.

Cреднее квадратическое отклонение
Выше уже было рассказано о формуле средней квадратической, которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:
Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:
В примере про студента, в котором выше рассчитали дисперсию, найдем среднее квадратическое отклонение как корень квадратный из нее:
.
Квадратический коэффициент вариации
В примере про студента, в котором выше рассчитали среднее квадратическое отклонение, найдем квадратический коэффициент вариации V = 0,707/4 = 0,177, что меньше критериального значения 0,333, значит вариация слабая и равна 17,7%.

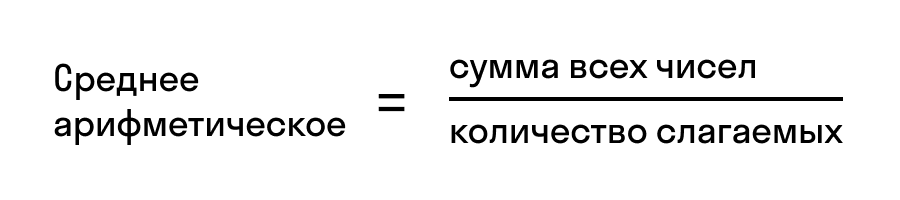



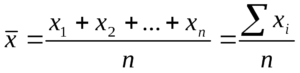
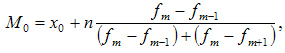
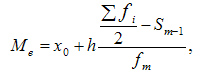




















 .
.