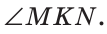Что значит сравнить отрезки

Как сравнить два отрезка: способы и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; АБ.

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Обратите внимание: что такое луч в геометрии.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

Сравнение в координатной сетке

Допустим, что у нас есть два отрезка, координаты которых мы знаем — а (Х1, Y1; Х2, Y2) и b (Х3, Y3; X4, Y4).

Первое, что нужно сделать — придать координатам числовые значения:

Da = √ ((-7 — 3) ² + (4 — (-4)) ²) = √ (-10 ² + 8 ²) = √ 100 + 64 = √ 164

Db = √ ((-3 — 0) ² + (-5 — (-3)) ²) = √ (-3 ² + (-8) ²) = √ (9+ 64) = √ 73

√ 164 > √ 73, значит, Da > Db.

Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.

Примеры

Рассмотрим сравнение методом наложения. У нас имеется два отрезка — АБ и ВГ.

Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.

Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБ 2, значит, CD>AB, то есть отрезок CD длиннее AB.

Источник

Отрезок

Обозначение отрезка.

На плоскости точка является одной из основных геометрических фигур (причем, самой малой).

Отметим на плоскости две произвольные точки А и В.

Соединим эти точки линией, приложив линейку.

Мы получили одну из простейших геометрических фигур на плоскости ‒ отрезок.

Произносится: отрезок АВ или отрезок ВА. Точки А и В называются концами данного отрезка.

Любые две точки на плоскости можно соединить отрезком (причем, только одним).

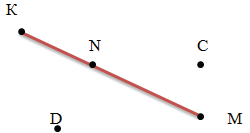
Точка N лежит на отрезке KM (между точками K и M), а точки C и D не лежат на отрезке KM.

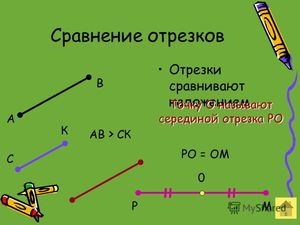
Сравнение отрезков

Отрезки можно сравнивать. Измерителем может служить количество клеток.

Отрезки AB и CD равны. Записывают это так: AB = CD.

На рисунке AB = CD = MK

Отрезок MK является частью отрезка MN.

Длина отрезка

Расстояние между точками M и N (концами отрезка MN) можно измерить с помощью линейки.

Длина отрезка MN равна 13 см, пишут: MN = 13 см.

Единицы измерения длины

Длину отрезка можно измерять не только в сантиметрах.

1 сантиметр содержит 10 миллиметров (1 см = 10 мм, миллиметр – это десятая часть сантиметра);

10 сантиметров ‒ это 1 дециметр (1 дм = 10 см);

100 сантиметров ‒ это 1 метр (1м = 100 см);

1 000 метров ‒ это 1 километр (1 км = 1 000 м).

Вопросы для самопроверки

Поделись с друзьями в социальных сетях:

Источник

Как сравнить длины отрезков?

Сравнить 2 отрезка на плоскости — это типичная задача по геометрии для учеников 7 класса. Существует несколько разных методов выполнения данного сравнения, и мы подробно расскажем о каждом из них.

Подобного рода задачи выполняются элементарно и являются основой для изучения дальнейшего материала. Стоит один раз запомнить этот несложный процесс, и в дальнейшем уже не возникнет никаких трудностей с аналогичными заданиями.

Метод наложения

Пусть нам даны два отрезка AB и СD:

Совместим начало отрезка AB и СD (точки A и С).

Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.

Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.

Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.

MK = KV, K — середина отрезка.

Рассмотрим еще одну пару отрезков HG и ST.

Совместим начало отрезка HG и ST.

Затем повернем отрезок STтак, чтобы он совпал с отрезком HG.

В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.

Вывод:

Измерение длин:

Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.

Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.

Наложим единичный отрезок на данные.

Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.

Сравним отрезки: QL > FJ (т.к. 5 > 3), FJ https://budu5.com/manual/chapter/3301

Как сравнить 2 отрезка: способы решения задачи

Что такое отрезок

Прежде чем рассказать, как сравнить 2 отрезка, давайте разберем, что такое отрезок на плоскости.

Определение из учебника по геометрии гласит, что отрезок — это часть прямой, которая с двух сторон ограничивается двумя точками.

Если рассматривать одну прямую, отрезком будет считаться множество, которое состоит из двух разных точек этой прямой (собственно, концов отрезка), а также остального множества из всех точек, которые располагаются между ними (так называемых внутренних точек).

Сравнение двух отрезков

Итак, в вопросе о том, как сравнить 2 отрезка, можно выделить следующие методы:

В том случае, если разность составит положительное число, значит, первый отрезок длиннее второго на соответствующее количество единиц. Если в результате получено нулевое значение — отрезки равны. А если в ответе отрицательное число, следовательно, второй отрезок длиннее первого.

Вывод

Итак, мы выяснили, как сравнить 2 отрезка. Первый способ указывает только на то, какой из них будет длиннее, а какой — короче, а второй показывает числовое значение разницы в длине.

Прямая и отрезок, измерение и сравнение отрезков

Понятие прямой, также как и понятие точки является основными понятиями геометрии. Как известно основные понятия не определяется. Это не является и исключением для понятия прямой. Поэтому рассмотрим суть этого понятия через его построение.

Возьмем линейку и, не отрывая карандаша, проведем линию произвольной длины.

Полученную линию мы и будем называть прямой. Однако тут необходимо отметить, что это не вся прямая, а только её часть. Всю же прямую построить не имеется возможным, она является бесконечной на обоих своих концах.

Прямые будем обозначать маленькой латинской буквой, либо двумя её точками в круглых скобках.

Понятия прямой и точки связаны тремя аксиомами геометрии:

Для двух прямых актуально их взаимное расположение. Возможны три случая:

В этой статье мы не будем подробно останавливаться на этих понятиях.

Отрезок

Пусть нам дана произвольная прямая и две точки, принадлежащие ей. Тогда отрезком будет называться часть прямой, которая ограничена двумя ее произвольными различными точками. Точки, которыми ограничен отрезок в рамках определения 1 называются концами этого отрезка.

Отрезки будем обозначать двумя её точками концов в квадратных скобках.

Сравнение отрезков

Рассмотрим два произвольных отрезка. Очевидно, что они могут быть либо равными, либо неравными. Чтобы разобраться в этом, нам нужна следующая аксиома геометрии.

Аксиома 4: Если оба конца двух различных отрезков совпадут при их наложении, то такие отрезки будут равными.

Итак, для сравнения выбранных нами отрезков (обозначим их отрезок 1 и отрезок 2) наложим конец отрезка 1 на конец отрезка 2, так, чтобы, отрезки оставались по одну сторону от этих концов. После такого наложения возможны два следующих случая:

Как сравнить длины отрезков: наложение и измерение, объяснение и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; АБ.

Это интересно: как разложить на множители квадратный трехчлен?

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

Источник

Содержание:

В практической деятельности для определения расстояния между пунктами находят длину отрезка, соединяющего рассматриваемые пункты. Если не принимать во внимание физические свойства предметов, то многие из них дают представление об отрезках, например карандаши, балки различных металлических конструкций и т. д.

Рассмотрим понятие отрезка. Для определения отрезка воспользуемся основным свойством (аксиомой) расположения точек на прямой, которое формулируется следующим образом:

Аксиома: Из трех точек на прямой единственная точка лежит между двумя другими.

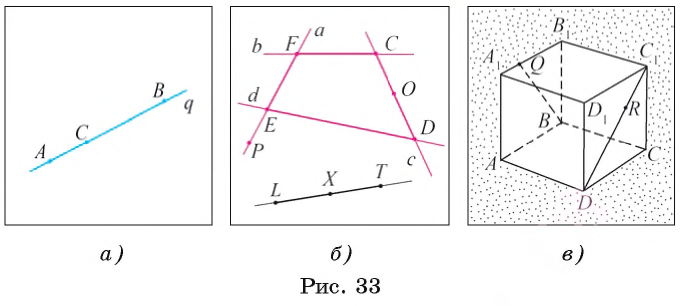
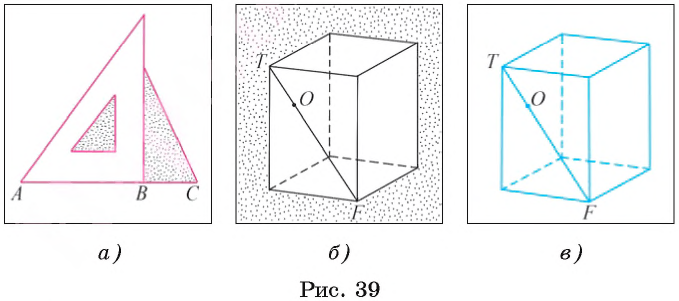
Пусть на прямой q лежат три точки А, В и С (рис. 33, а). Точка С лежит между точками А и В. Можно говорить также, что точки А и В лежат по разные стороны от точки С или что точки А и С лежат по одну сторону от точки Б.

Определение. Отрезком называется геометрическая фигура, состоящая из двух точек прямой и всех ее точек, лежащих между данными точками.

Данные точки называются концами отрезка, остальные его точки называются внутренними точками.

Отрезок, концами которого являются точки А и В, обозначается АВ или ВА. Иногда отрезки обозначаются также строчными буквами латинского алфавита а, b, с и т. д.

Если точки А и B — концы отрезка АВ, то говорят, что отрезок АВ соединяет эти точки.

Можно сказать, что отрезок АВ есть фигура, состоящая из двух точек А, В и части прямой, ими ограниченной.

Подчеркнем, что отрезок LТ состоит из точек L, T и всех точек X прямой LТ, лежащих между точками L и Т (рис. 33, б).

Например, на рисунке 33, B изображены отрезки ЕF, FС, СD и DЕ, которые лежат на прямых а, b, с и d соответственно.

Точка О является внутренней точкой отрезка СD, а точка Р не является внутренней точкой отрезка ЕF. На рисунке 33, в изображены отрезки BQ и DC₁, которые лежат в гранях куба, и точка R, являющаяся внутренней точкой отрезка DC₁.

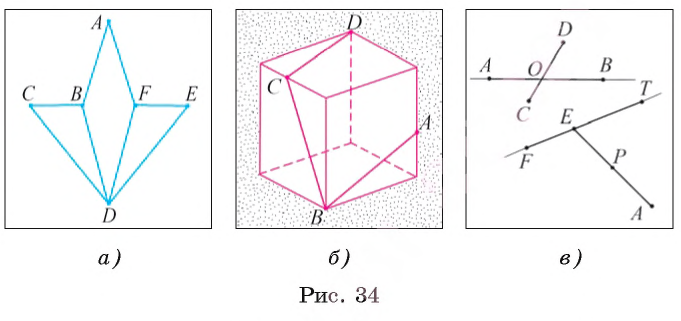
Пользуясь отрезками, мы можем конструировать новые геометрические фигуры. Например, на рисунке 34, а изображена фигура, образованная отрезками АВ, ВС, СD, DЕ, DB, DF, ЕF, FА.

На рисунке 34, B изображен куб и геометрическая фигура, образованная отрезками АВ, ВС, СD, которые лежат в гранях этого куба.

На рисунке 34, в изображены отрезки АВ и СD, которые пересекаются в точке О. Точка О является внутренней точкой каждого из этих отрезков.

Отрезки FТ и ЕА, изображенные на рисунке 34, в, имеют общую точку Е. Точка Е одновременно является внутренней точкой отрезка FТ и концом отрезка ЕА.

Если отрезок АВ не пересекает прямую l, то говорят, что точки А и В лежат по одну сторону от прямой l.

Например, точки Р и А лежат по одну сторону прямой FТ, так как отрезок РА и прямая FТ не пересекаются (см. рис. 34, в).

Если отрезок АВ пересекается с прямой l во внутренней точке отрезка АВ, то говорят, что точки А и В лежат по разные стороны от прямой l.

Например, точки С и D лежат по разные стороны от прямой АВ (см. рис. 34, в).

Более подробное объяснение:

Прямую можно представить как туго натянутую нить, бесконечную в обе стороны. Прямая изображается отрезком, который может быть продолжен в обе стороны.

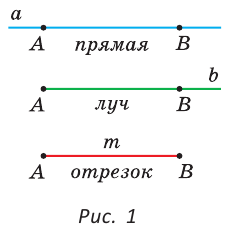
Луч и отрезок — это части прямой. Луч можно представить как луч от фонарика, а отрезок — как карандаш. Луч состоит из точки прямой (начало луча) и всех ее точек, лежащих по одну сторону от данной точки. Отрезок состоит из двух точек прямой (концов отрезка) и всех ее точек, лежащих между двумя данными точками.

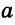
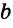
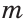
На рисунке 1 показаны: прямая АВ (или ВА, или ), луч АВ (или ), отрезок АВ (или ВА, или ). При назывании или записи луча двумя буквами на первом месте ставится начало луча.

Измерение отрезков

Для сравнения отрезков их можно наложить друг на друга. Если отрезки совпадут своими концами, то они равны, если нет — то отрезок, который лежит внутри другого отрезка, считается меньшим. На рисунке 2 отрезок АВ меньше отрезка CD, то есть АВ а и говорят: «Отрезок b больше отрезка а».

Например, на рисунке 38, B отрезок АQ составляет часть отрезка АF, отрезок КЕ — часть отрезка КР.

Если точка С является внутренней точкой отрезка АВ, то говорят, что она разбивает, или делит, отрезок на два отрезка АС и СВ.

Например, на рисунке 38, в точка F разбивает отрезок ОЕ на отрезки ОF и FЕ, а точка Т разбивает отрезок ЕF на отрезки ЕТ и ТF.

В дальнейшем будем предполагать, что выполняется следующая аксиома.

Аксиома откладывания отрезка. На любом луче от его начала можно отложить единственный отрезок, равный данному.

Эта аксиома означает, что если дан какой-либо отрезок АВ и произвольный луч h с началом в точке О, то на луче h существует единственная точка X, такая, что отрезок ОХ равен отрезку АВ.

Серединой отрезка называется точка, делящая его на два равных отрезка.

Например, на рисунке 38, B изображена точка О — середина отрезка ТR (О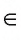ТR, ТО = ОR).

Измерение длин отрезков

В практической деятельности часто необходимо измерять длины отрезков. Знание длин отрезков позволяет сравнивать их, не накладывая один на другой.

Измерение длин отрезков основано на сравнении их с некоторым отрезком, который принимается за единицу измерения (единичный отрезок).
Длина отрезка — это геометрическая величина, которая показывает, сколько раз единица измерения и ее части укладываются в измеряемом отрезке.

Длина отрезка АВ обозначается АВ.

Длина отрезка может измеряться в миллиметрах (мм), сантиметрах (см), дециметрах (дм), метрах (м) и т. д.

Например, если за единицу измерения принять отрезок в 1 см, то для определения длины отрезка необходимо узнать, сколько раз в измеряемом отрезке укладывается сантиметр и его части.

Если в отрезке АВ отрезок в 1 см укладывается 3 раза, то говорят, что отрезок АВ имеет длину, равную 3 см, и пишут: АВ = 3 см. Если в отрезке CD сантиметр укладывается 2 раза и в остатке 5 раз укладывается десятая часть сантиметра, то длина отрезка СD равна 2,5 см, т. е. СD = 2,5 см.

При выбранной единице измерения длину отрезка можно выразить некоторым положительным числом. Если два отрезка равны, то единичный отрезок и его части укладываются в этих отрезках одинаковое число раз, т. е. равные отрезки имеют равные длины.

При измерении отрезков опираются на следующие свойства длины отрезков.

Длиной ломаной называется сумма длин ее звеньев.

Теперь дадим определение расстояния между точками.

Определение. Расстоянием между двумя точками называется длина отрезка, соединяющего данные точки.

Если две точки совпадают, то расстояние между ними считается равным нулю.

Расстояние между двумя точками А и B обозначается АB или ВА.

Пример:

Точка B делит отрезок АС на два отрезка АВ и ВС. Вычислите длину отрезка АС, если известно, что АB = 2 см, а ВС = 1 см (рис. 39, а).

Длина отрезка АС равна сумме длин отрезков, на которые он делится точкой B. Следовательно, АС=АВ + ВС = 2+1 = 3 (см).

Пусть точка О делит отрезок ТF — диагональ грани прямоугольного параллелепипеда — на отрезки ТО и ОF (рис. 39, б, в).

Окружность и круг

Дадим определение еще одной геометрической фигуры.

Определение. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, находящихся на заданном расстоянии от данной точки этой плоскости.

Данная точка называется центром окружности.

Радиусом окружности называется отрезок, соединяющий центр окружности с какой-либо точкой окружности.

Иногда радиусом окружности называют длину отрезка, соединяющего центр окружности с какой-либо ее точкой.

Из определения следует, что все радиусы окружности равны.

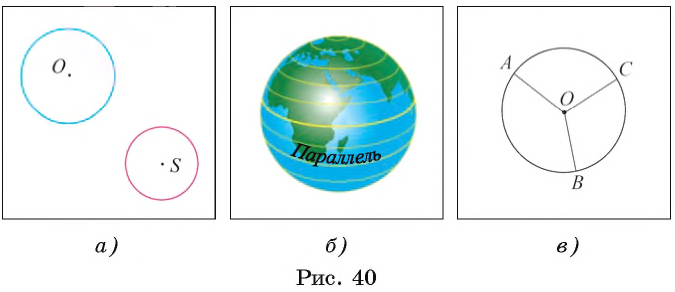
На рисунке 40, а изображены окружности с центрами в точках О и S. Параллели имеют форму окружностей, расположенных на поверхности земного шара (рис. 40, б).

Например, на рисунке 40, в изображены радиусы ОА, ОВ и ОС. Окружность с центром в точке О и радиусом R обозначается 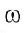(O, R) (читают: «Окружность с центром в точке О и радиусом R»).

Хордой окружности называется отрезок, соединяющий две точки окружности.

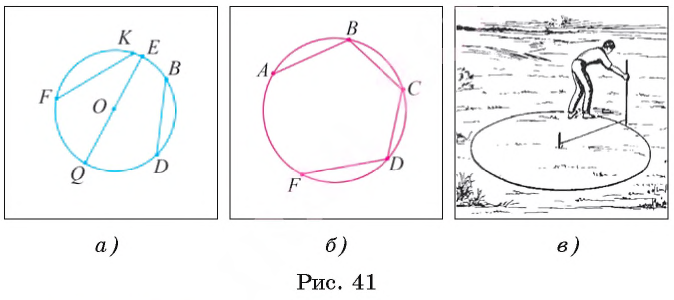
Например, на рисунке 41, а изображены хорды FК, DB и QЕ, а на рисунке 41, B изображена ломаная АВСDF, каждое звено которой является хордой окружности.

Диаметром окружности называется хорда, проходящая через центр окружности (или длина такой хорды). Центр окружности делит любой ее диаметр на два равных отрезка.

Например, хорда QЕ является диаметром окружности, так как проходит через центр О этой окружности (см. рис. 41, а).

Дугой окружности называется каждая из частей, на которые делят окружность любые две ее точки.

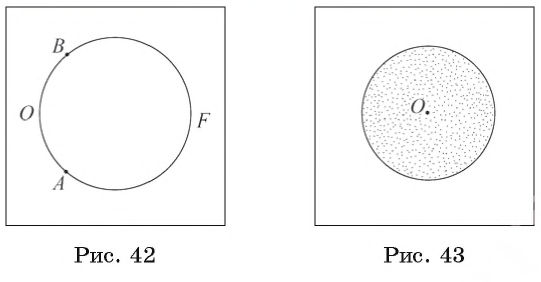
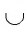
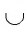
Например, на рисунке 42 точки А и B делят окружность на две дуги АОВ и АFB, которые обозначаются АОВ и AFB (читают: «Дуга АОВ и дуга АFB»).

Прочертить окружность на местности для разбивки цветочной клумбы можно с помощью веревки и колышка (рис. 41, в).

Определение. Кругом называется геометрическая фигура, состоящая из окружности и части плоскости, ограниченной этой окружностью (рис. 43).

Окружность называется границей круга.

Круг с центром в точке О и радиусом R обозначается 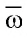(О, R) (читают: «Круг с центром в точке О и радиусом R»).

Окружность с центром в точке О и радиусом R называется границей круга с центром в точке О и радиусом R.

Центром, радиусом, хордой и диаметром круга называются центр, радиус, хорда и диаметр его границы.

Плоская геометрическая фигура называется ограниченной, если все ее точки принадлежат некоторому кругу, и называется неограниченной, если не существует круга, содержащего все точки этой фигуры.

Любой отрезок АВ — ограниченная фигура, так как для него существует круг некоторого, быть может, достаточно большого радиуса, которому принадлежат все точки этого отрезка. Например, любой отрезок АВ принадлежит кругу с центром в точке А и радиусом R=АВ.

Примером неограниченной фигуры является любая прямая или луч. Не существует круга, которому принадлежат все точки прямой. Для круга сколь угодно большого радиуса найдутся точки прямой, которые не принадлежат этому кругу.

Сравнение и измерение углов

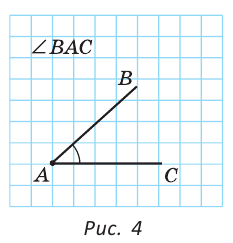
Если из точки провести два луча, то получим угол. Эти лучи называются сторонами угла, а их общая точка — его вершиной. При записи угла тремя большими буквами вершина угла записывается в центре.

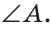
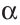
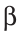
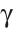
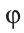
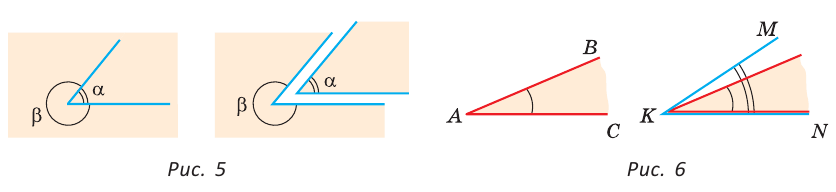
На рисунке 4 лучи АВ и АС — стороны угла ВАС (или CAB), точка А — вершина угла. Если понятно из рисунка, о каком угле идет речь, то его обозначают одной буквой при вершине угла: Часто углы обозначают числами, поставленными внутри угла у его вершины, или малыми буквами греческого алфавита: (альфа), (бета), (гамма), (фи). Обычно равные углы на чертеже обозначают равным числом дуг.

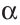
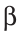
Угол, изображенный на плоскости, делит ее на две части, каждая из которых называется плоским углом. На рисунке 5 это углы и . Далее мы будем рассматривать плоские углы. Слово «плоский» при названии углов употреблять не будем.

Сравнить углы можно наложением, совместив сторону одного угла со стороной другого. Если углы совпадут, то они равны; если нет, то угол, который лежит внутри другого угла, считается меньшим. На рисунке 6 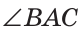меньше, чем

Измерение углов

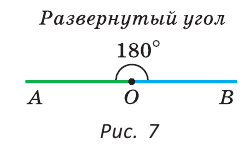
Если стороны угла повернуть вокруг его вершины так, чтобы они образовали прямую, то получим развернутый угол (рис. 7).

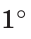
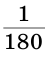
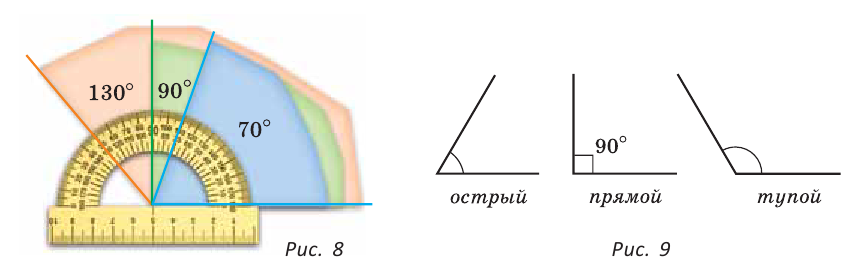
Углы можно сравнить, измерив их величины. Углы измеряются в градусах. Величину развернутого угла принимают за 180°. Тогда — это часть развернутого угла, которая получится, если из его вершины провести лучи, делящие развернутый угол на 180 равных частей. Углы измеряют при помощи транспортира (рис. 8). Транспортир также позволяет построить угол данной градусной меры.

Виды углов: угол, меньший 90°, называется острым; равный 90°, — прямым; больший 90°, но меньший 180°, — тупым углом (рис. 9).

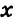
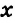
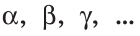
Неизвестный угол при решении задач иногда обозначают или °. Буквами обозначают и угол, и его градусную меру.

Полуплоскость

Пусть l — некоторая прямая на плоскости. Тогда эта прямая разделяет множество остальных точек плоскости на два множества, каждое из которых вместе с прямой l называется полуплоскостью. Прямая l называется границей каждой из полуплоскостей.

Полуплоскость с границей l характеризуется следующим образом. Если две точки лежат по одну сторону от прямой l, то эти точки лежат в одной полуплоскости с границей l. Если две точки лежат по разные стороны от прямой l, то эти точки лежат в разных полуплоскостях с границей l.

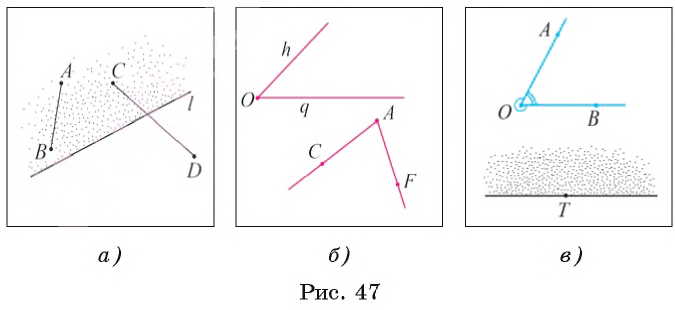
Например, точки А и В лежат в одной полуплоскости с границей l, а точки С и D лежат в разных полуплоскостях с границей l (рис. 47, а).

Определение. Полуплоскостью называется геометрическая фигура, состоящая из прямой и всех точек плоскости, лежащих по одну сторону от данной прямой.

Данная прямая называется границей полуплоскости.

Угол и его определение

Пусть на плоскости даны два луча h, q, имеющие общее начало О. Тогда остальные точки плоскости разделяются этими лучами на две части, каждая из которых вместе с лучами h и q называется углом (рис. 47, б).

Определение. Углом называется геометрическая фигура, состоящая из двух лучей с общим началом и одной из частей плоскости, на которые эти лучи разделяют остальные точки плоскости.

Лучи называются сторонами угла, а их общее начало — вершиной угла.

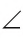
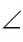
Угол с вершиной О и сторонами h, q обозначается hq или O (говорят: «Угол hq» или «Угол О»).

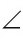
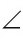
Если на сторонах угла с вершиной А указаны, например, точки С и F, тогда этот угол можно обозначать CAF или FАС (см. рис. 47, б).

Заметим, что два луча с общим началом являются сторонами двух углов. Тот из углов, который хотят рассматривать, на рисунке отмечается дугой.

На рисунке 47, в дугой отмечен один из углов, а двумя дугами — другой из углов, сторонами которых служат лучи ОА и ОВ.

Развернутым углом называется угол, стороны которого являются противоположными лучами. На рисунке 47, в изображен развернутый угол с вершиной Т.

Если два луча с общим началом совпадают, то говорят, что они являются сторонами нулевого угла.

Для каждого ненулевого угла определены его внутренняя и внешняя области. Внутренней областью угла называется множество точек этого угла, не принадлежащих его сторонам.

Внешней областью угла называется множество точек плоскости, не принадлежащих углу.

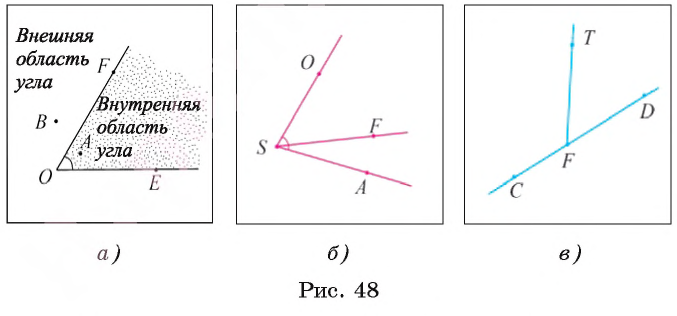
На рисунке 48, а показаны точка А, которая лежит во внутренней области неразвернутого угла FOE, и точка В, лежащая во внешней области этого угла.

Если начало луча совпадает с вершиной угла и луч лежит во внутренней области данного угла, то говорят, что этот луч делит угол на два угла.

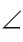
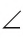
Например, на рисунке 48, B луч SF делит угол ASO на два угла: ASF и FSO.

Любой луч с началом в вершине развернутого угла, не совпадающий с его сторонами и лежащий в его внутренней области, делит этот развернутый угол на два угла.

Например, луч FT, не совпадающий с лучами FC и FD, делит развернутый угол CFD с вершиной F на два угла: CFT и TFD (рис. 48, в).

Сравнение углов

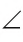
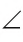
Пусть 1 и 2 — два неразвернутых угла (рис. 49, а). Для сравнения этих углов наложим один угол на другой так, чтобы сторона одного угла совместилась со стороной другого, а две другие стороны были расположены в одной полуплоскости.

Если две другие стороны также совместятся, то совместятся и сами углы, а следовательно, они равны. Если при наложении эти стороны не совместятся, то меньшим считается тот угол, который является частью другого угла.

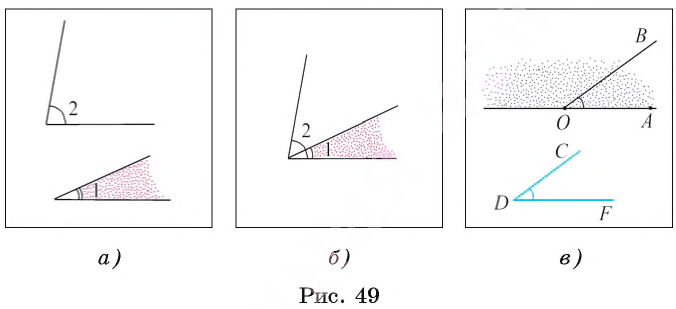
Например, на рисунке 49, B 1 составляет часть 2, поэтому l меньше 2 (в этом случае пишут, что 1 l и читают: «Угол 1 меньше угла 2» или «Угол 2 больше угла 1»).

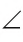
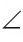
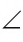
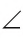
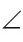
Если угол неразвернутый, то он может быть меньше или больше развернутого.

В дальнейшем, если не будет оговорено иное, будем рассматривать углы, меньшие развернутого угла или развернутые.

Далее будем пользоваться следующей аксиомой.

Аксиома откладывания угла в данную полуплоскость. От любого луча в данную полуплоскость можно отложить единственный угол, равный данному неразвернутому углу.

Эта аксиома означает, что если дан какой-либо луч OA и некоторый угол CDF, то в каждой из двух полуплоскостей, границей которой является прямая ОА, существует единственный луч ОВ, такой, что угол CDF равен углу АОВ (рис. 49, в).

Определение. Биссектрисой угла называется луч с началом в вершине этого угла и делящий его на два равных угла.

Измерение углов

Измерение углов основано на сравнении их с некоторым углом, который принимается за единицу измерения. За единицу измерения углов принят угол в один градус (градус) — угол, равный 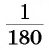части развернутого угла.

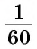
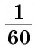
Некоторые части градуса имеют специальное название. Например, часть градуса называется минутой и обозначается знаком «’», а часть минуты называется секундой и обозначается знаком «»».

Градусная мера угла — это геометрическая величина, которая показывает, сколько раз угол в один градус и его части укладываются в данном угле.

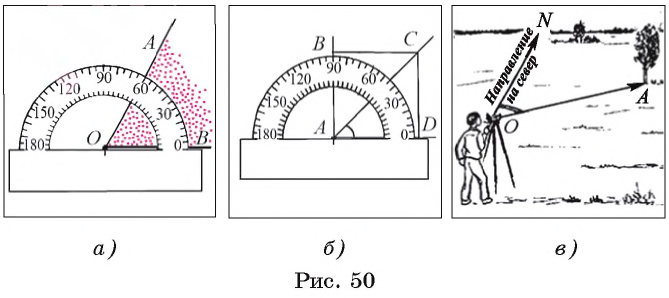
Для измерения углов используется транспортир (рис. 50, а).

Например, на рисунке 50, а изображен угол АОВ, градусная мера которого равна 60°. На рисунке 50, B изображен угол CAD, градусная мера которого равна 45° и BAD=90°.

Угол, градусная мера которого равна 35 градусов 40 минут и 12 секунд, обозначают следующим образом: 35°40’12».

Так как градус составляет 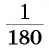развернутого угла, то градусная мера развернутого угла равна 180°. Градусная мера нулевого угла считается равной 0°.

Каждый угол имеет определенную градусную меру.

Если два угла равны, то угол в один градус и его части укладываются в этих углах равное число раз, т. е. равные углы имеют равные градусные меры.

Если один угол меньше другого, то угол в один градус или его части укладываются в нем меньшее число раз, чем в другом угле.

При измерении углов опираются на следующие свойства градусной меры углов.

Понятие угла и его градусной меры используется на практике, например при определении курса корабля или в геодезии при определении азимута предмета — градусной меры угла между направлением на север и направлением на предмет (рис. 50, в).

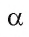
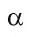
Если дан угол, градусная мера которого равна , то можно говорить, что «дан угол, равный ».

Угол называется прямым, если его градусная мера равна 90° (рис. 51, а), острым — если больше 0° и меньше 90° (рис. 51, б), тупым — если больше 90° и меньше 180° (рис. 51, в).

Ранее мы обсуждали, что понимается под теоремой. Теперь докажем теоремы, которые характеризуют свойства смежных и вертикальных углов.

Свойства смежных и вертикальных углов

Два угла называются смежными, если у них одна сторона общая, а две другие стороны этих углов являются противоположными лучами.

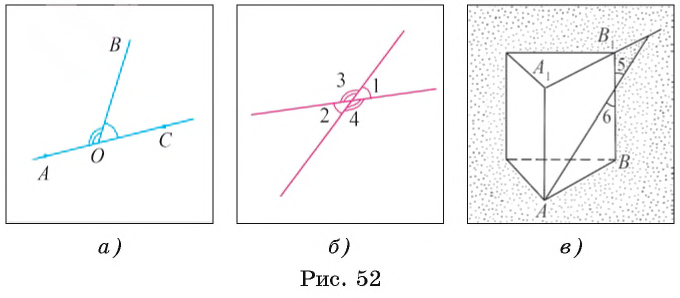
Например, углы АОВ и ВОС, изображенные на рисунке 52, а, являются смежными.

Два угла называются вертикальными, если они имеют общую вершину и стороны одного угла являются лучами, противоположными сторонам другого.

Например, на рисунке 52, B изображены вертикальные углы 1 и 2, 3 и 4. На рисунке 52, в изображены вертикальные углы 5 и 6, лежащие в той же плоскости, в которой лежит грань АВВ₁А₁ прямой призмы.

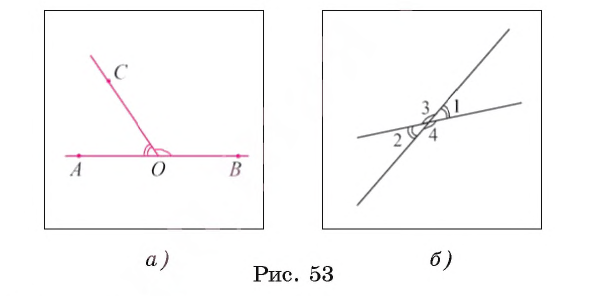
Теорема 1 (о свойстве смежных углов). Сумма градусных мер смежных углов равна 180°.

Пусть углы АОС и ВОС смежные (рис. 53, а). Так как луч ОС делит развернутый угол с вершиной О на два угла АОС и BОС, то AOC + BOC = AOB.

А поскольку AOB = 180°, то AOC + BOC = 180°.

Теорема 2 (о свойстве вертикальных углов). Вертикальные углы равны.

Перпендикулярные прямые

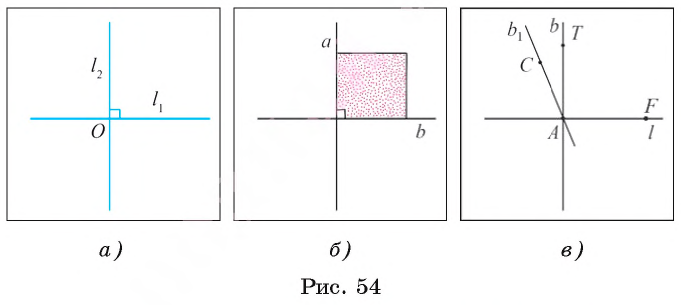
Теперь рассмотрим понятие перпендикулярных прямых. Пусть две прямые l₁ и l₂ пересекаются в точке О. При этом образуются четыре неразвернутых угла, сторонами которых являются лучи данных прямых с началом в точке О. Если один из этих углов прямой (рис. 54, а), то, как следует из теорем 1 и 2, и остальные углы также прямые. В этом случае говорят, что прямые l₁ и l₂ при пересечении образуют прямые углы.

Определение. Две прямые называются перпендикулярными (или взаимно перпендикулярными), если они при пересечении образуют прямые углы.

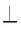
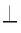
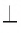
Если прямые а и b (АВ и СD) перпендикулярные, то используется обозначение а b (АВ СD). Запись а b читают следующим образом: «Прямая а перпендикулярна прямой b».

Лучи и отрезки называются перпендикулярными, если они лежат на перпендикулярных прямых.

Отрезок называется перпендикулярным прямой, если он лежит на прямой, перпендикулярной данной прямой.

На рисунке 54, B изображены перпендикулярные прямые а и b, содержащие две стороны квадрата.

Теорема 3. Через каждую точку прямой в плоскости проходит единственная прямая, перпендикулярная данной прямой.

1. Докажем, что такая прямая существует.

Пусть l — данная прямая, А — произвольная точка прямой l. Пусть AF — один из лучей этой прямой с началом в точке А.

На основании аксиомы откладывания угла отложим от луча AF прямой угол TAF. Тогда прямая b, содержащая луч AT, перпендикулярна прямой l (рис. 54, в).

2. Докажем, что такая прямая единственная.

Допустим, что существует еще одна прямая b₁, проходящая через точку А и перпендикулярная прямой l.

Пусть АС — луч этой прямой, лежащий в одной полуплоскости с лучом AT. Каждый из углов FAT и FAC — прямой и отложен от данного луча в одной полуплоскости.

Согласно аксиоме откладывания угла, от данного луча в данную полуплоскость можно отложить только один прямой угол. Следовательно, не может быть другой прямой, проходящей через точку А и перпендикулярной прямой l.

Доказательство от противного

При доказательстве предыдущей теоремы применялся способ, который называется доказательством от противного.

Этот способ доказательства состоит в том, что сначала делают предположение о верности утверждения, противоположного тому, которое необходимо доказать. Затем путем рассуждений, опираясь на аксиомы и доказанные ранее теоремы, приходят к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании делают вывод, что сделанное предположение было неверным, а, следовательно, верно утверждение теоремы.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник