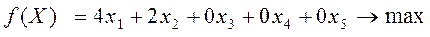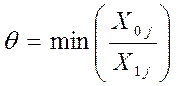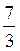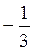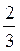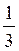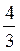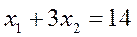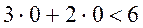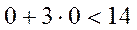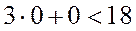Что значит составить математическую модель задачи
Что такое математическая модель?
Понятие математической модели.
Например, нам нужно посчитать расходы (Р) на покупки в магазине. Надо купить две булки (Б) и три пачки масла (М). Мы знаем цену булки (ЦБ) и цену масла (ЦМ). Легко можно записать:
Составление (построение) математической модели задачи.
Говоря конкретнее, нужно установить математическую связь между всеми данными задачи.
Но можно выделить три основных момента, на которые нужно обратить внимание.
1. В любой задаче есть текст, как ни странно.) В этом тексте, как правило, имеется явная, открытая информация. Числа, значения и т.п.
3. В любой задаче должно быть дана связь данных между собой. Эта связь может быть дана открытым текстом (что-то равно чему-то), а может быть и скрыта за простыми словами. Но простые и понятные факты частенько упускаются из виду. И модель никак не составляется.
Сразу скажу: чтобы применить эти три момента, задачу приходится читать (и внимательно!) несколько раз. Обычное дело.
Начнём с простой задачки:
Все эти слова нужно превратить в какое-то уравнение. Для этого нужно, повторюсь, установить математическую связь между всеми данными задачи.
С чего начинать? Сначала вытащим из задачи все данные. Начнём по порядочку:
Обращаем внимание на первый момент.
Какая здесь явная математическая информация? 8 рыбин и 20%. Не густо, да нам много и не надо.)
Обращаем внимание на второй момент.
Ищем скрытую информацию. Она здесь есть. Это слова: «20% всех рыбин«. Здесь нужно понимать, что такое проценты и как они считаются. Иначе задача не решается. Это как раз та дополнительная информация, которая должна быть в голове.
Здесь ещё имеется математическая информация, которую совершенно не видно. Это вопрос задачи: «Сколько всего рыбин купил. « Это ведь тоже какое-то число. И без него никакая модель не составится. Поэтому обозначим это число буквой «х». Мы пока не знаем, чему равен икс, но такое обозначение очень нам пригодится. Подробнее, что брать за икс и как с ним обращаться, написано в уроке Как решать задачи по математике? Вот так сразу и запишем:
Возвращаемся к раскрытию информации. Кто не знает, что такое процент, никогда не раскроет, да. А кто знает, тот сразу скажет, что проценты здесь от общего числа рыб даны. А нам это число неизвестно. Ничего не выйдет!
Общее количество рыб (в штуках!) мы не зря буквой «х» обозначили. Посчитать южных рыб в штуках не получится, но записать-то мы сможем? Вот так:
Вот теперь мы скачали всю информацию с задачи. И явную, и скрытую.
Обращаем внимание на третий момент.
Ищем математическую связь между данными задачи. Эта связь настолько проста, что многие её не замечают. Такое часто бывает. Здесь полезно просто записать собранные данные в кучку, да и посмотреть, что к чему.
Вот это уравнение и будет математической моделью нашей задачи.
Прошу заметить, что в этой задаче нас не просят ничего складывать! Это мы сами, из головы, сообразили, что сумма южных и северных рыб даст нам общее количество. Вещь настолько очевидная, что проскакивает мимо внимания. Но без этой очевидности математическую модель не составить. Вот так.
Теперь уже можно применить всю мощь математики для решения этого уравнения). Именно для этого и составлялась математическая модель. Решаем это линейное уравнение и получаем ответ.
Составим математичесскую модель ещё одной задачки:
Спросили Петровича: «А много ли у тебя денег?» Заплакал Петрович и отвечает: «Да всего чуть-чуть. Если я потрачу половину всех денег, да половину остатка, то всего-то один мешок денег у меня и останется. » Сколько денег у Петровича?
Опять работаем по пунктам.
2. Ищем скрытую информацию. Это половинки. Чего? Не очень понятно. Ищем дальше. Есть ещё вопрос задачи: «Сколько денег у Петровича?» Обозначим количество денег буквой «х»:
И вновь читаем задачу. Уже зная, что у Петровича х денег. Вот тут уже и половинки сработают! Записываем:
Остаток будет тоже половина, т.е. 0,5·х. А половину от половины можно записать так:
Теперь вся скрытая информация выявлена и записана.
3. Ищем связь между записанными данными. Здесь можно просто читать страдания Петровича и записывать их математически):
Если я потрачу половину всех денег.
да половину остатка.
Отнимем ещё половину остатка:
то всего-то один мешок денег у меня и останется.
А вот и равенство нашлось! После всех вычитаний один мешок денег остаётся:
Вот она, математическая модель! Это опять линейное уравнение, решаем, получаем:
Задачки, конечно, элементарные. Это специально, чтобы уловить суть составления математической модели. В некоторых задачах может быть гораздо больше данных, в которых легко запутаться. Это часто бывает в т.н. компетентностных задачах. Как вытаскивать математическое содержание из кучи слов и чисел показано на примерах здесь.
В задачах на движение требуется держать в голове формулу-ключ: связь расстояния, скорости и времени. По ссылке можно посмотреть примеры составления модели и решения таких задач.
В задачах на работу надо чётко понимать формулу-ключ: связь времени, производительности труда и объёма работы. Там имеются свои фишки, с которыми можно ознакомиться по ссылке.
Для того, чтобы свободнее ориентироваться в построении математических моделей очень полезно порешать обратные задачи. Т.е. по заданной модели придумать условие задачи. Это, кстати, не так просто.) Тема может быть совершенно любой, фантазия ограничена только математикой. Вот примеры таких заданий:
Составить задачу по математической модели:
х + (х+10) + (х-30) + 20 = 120
Попробуйте придумать задачку, а потом можете найти в уроке Как решать задачи по математике исходную задачу для этой модели. И сравните, для интереса.)
Еще пример, посложнее:
Составить задачу по математической модели:
Исходная задача и её решение приведены в уроке Решение задач на движение. Кстати, по ссылке подробно написано, как эту математическую модель составить.
Составить задачу по математической модели:
1 = 5 · (х + 2х + 2х + 3х + 4х)
Эта задача и её решение расписаны в уроке Задачи на работу.
Ещё одно замечание. В классических школьных задачах (трубы заполняют бассейн, куда-то плывут катера и т.п.) все данные, как правило, подобраны очень тщательно. Там выполняются два правила:
— информации в задаче хватает для её решения,
— лишней информации в задаче не бывает.
В компетентностных и прочих жизненных задачах эти правила строго не соблюдаются. Нету подсказки. Но и такие задачи можно решать. Если, конечно, потренироваться на классических.)
Если Вам нравится этот сайт.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
А вот здесь можно познакомиться с функциями и производными.
Математическая модель
Что такое математическая модель
Математическая модель — концепция представления реальности математическим способом, вариант схемы как комплекса, изучение которого позволяет человеку обрести знания о некой другой системе.
Простой пример: график зависимости среднесуточной температуры от времени.
Математическая модель также была создана для того, чтобы проанализировать и предугадать поведение материального объекта. Однако у математической модели есть проблема, от которой не избавиться — идеализация.
Математическое моделирование — процесс создания, а также приемы построения и исследования математических моделей.
Все науки, которые используют для решения своих задач математический аппарат, практикуют математическое моделирование. То есть, заменяют объект своего исследования математической моделью и занимаются исследованием последней.
При помощи совокупности математических методов можно описать образцовый объект или процесс, который построен на стадии содержательного моделирования.
Как осуществляется связь математической модели и реальности?
Самые важные математические модели всегда обладают качеством универсальности. То есть, совершенно разные феномены могут быть описаны одной математической моделью.
Однако стоит помнить, что модель — объект, она может иметь собственные качества и свойства, которые могут не относиться к реальному моделируемому объекту.
Часто математические модели представляют в виде:
Представим основные понятия, которые важны для изучения данной темы:
Виды математических моделей, классификация
Существует несколько классификаций математических моделей. Рассмотрим некоторые из них.
Формальная типология
Основа данной классификации — какие математические средства используются для создания модели. Для создания схем в формальной классификации часто используется прием дихотомии.
Дихотомия — раздвоение, разделение чего-то на две части. Например, графиков.
К известным типам дихотомии относятся:
| Линейные | Нелинейные |
| Сосредоточенные | Распределенные |
| Детерминированные | Стохастические |
| Статические | Динамические |
| Дискретные | Непрерывные |
Типология по методу представления объекта
В рамках данной классификации выделяют структурные и функциональные модели.
Эти парадигмы также имеют название «черные ящики».
Содержательные, а также формальные модели
Многие авторы, которые описывают процесс моделирования в математике, отмечают, что для начала нужно построить специальную образцовую конструкцию, так называемую содержательную модель.
В разных учебных изданиях идеальный объект называется по-разному. Встречаются такие примеры как умозрительная модель, концептуальная модель, а также предмодель.
Конечная математическая схема будет назваться формальной моделью (математическая модель). Она получается в результате представления предмодели с помощью формального языка.
Построить умозрительную модель можно с помощью уже готового набора идеализаций. Например, в механике существуют идеальные пружины, маятники, твердые тела и тд, которые представляют собой готовые заготовки для построения содержательной модели.
Однако есть научные области, в которых сложно построить содержательные модели, потому что в них нет полноценных формализованных доктрин. К таким дисциплинам относятся биология, физика, психология, экономика и многие другие).
Содержательная типология
В работах английского физика Рудольфа Эрнста Пайерлса можно найти некоторые типологии математических моделей, которые используются в физике и других естественных науках. Советские ученые Александр Горбань и Рэм Хлебопрос расширили классификацию Пайерлса. Данная типология акцентирует свое внимание на процессе выстраивания содержательной модели. Итак, существуют следующие типы математических моделей:
Сложность моделируемой системы
Выделяются три уровня систем по сложности:
Советский академик Александр Андронов выделил три типа неустойчивых моделей:
Неустойчивые модели называют негрубыми. Устойчивые модели — мягкие.
Какие еще бывают модели?
Это ряд прототипов, которые выделяются по принципу применения.
Также выделяют материальные и информационные модели. Натуральные — муляжи, макеты. А информационные — прототипы, которые заменяют реальность формально (то есть словесно, графически и т.д.).
Какие параметры нужны для построения математической модели
Рассмотрим принципы построения математических моделей:
Также все математические модели должны отличаться следующими признаками адекватностью, конечностью, полнотой, упрощенностью, гибкостью.
Алгоритм составления, основные моменты
Для того чтобы составить математическую модель необходимо перевести данные задачи в вид математической формы. То есть переделать слова в формулу, уравнение и т.д. Необходимо установить математические связи между всеми условиями задачи.
Стоит помнить, что формула, уравнение математической модели должно полностью соответствовать тексту задачи, потому что иначе цель исследования изменится, а значит и задачу мы будем решать другую.
Представим алгоритм решения математической модели:
Попробуем составить математическую модель на примере простой задачи:
Иван Федорович вернулся с охоты и показал своей семье добычу. Оказалось, что он принес 10 тушек зайцев, которые живут в тайге, 50 % всей добычи — из тундры, а из местного леса, где охотился Иван Федорович нет ни одного животного. Сколько всего дичи купил Иван Федорович в магазине «Мясо диких животных?».
Данный текст нужно представить в виде уравнения. Для этого необходимо установить математические связи между всеми условиями задачи.
Обобщение — для того, чтобы построить математическую модель, нужно выбросить всю ненужную информацию из задачи, оставить только нужное и заменяем на математический объект.
Составление математической модели задачи и её решение симплекс-методом и графическим методом. Расчет оптимальной стратегии и цены игры, заданной платежной матрицей
Страницы работы
Содержание работы
1-20. Составить математическую модель задачи и решить ее двумя способами: симплекс-методом и графически. Для полученной задачи составить двойственную и проверить оптимальность плана исходной задачи с помощью критериев оптимальности планов двойственных задач.
Решение: Составить математическую модель по данной таблице:
Технолог. Способы I II
Составить план использования технологических способов в производстве, обеспечивающих максимальную прибыль.
Математическая модель задачи:
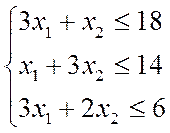
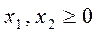
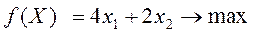
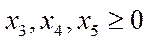
Введем дополнительные неизвестные и прибавим их к левым частям неравенств (I), тогда получим основную задачу:
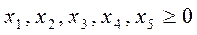

Основная задача (IV)-(VI) является канонической и поэтому ее можно решить симплекс-методом.
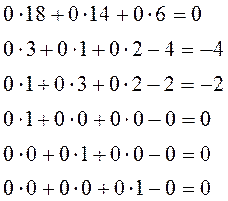
Обозначим: ключевая строка: s=3
ключевой столбец: r=1
Задача считается решенной, если все элементы индексной строки неотрицательны. У нас это условие не выполнено, это означает, что исходный базис можно улучшить, построив новую таблицу. По табл.1 базисный план X1=(0,0,18,14,6), для которого значение целевой функции f(X1)=0.
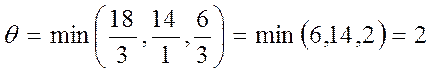
Это означает, что нас интересует 3 строка, поэтому строка с неизвестным x5 выводится из базиса. На пересечении ключевого столбца и ключевой строки стоит элемент 3 (в табл.1 выделен зеленым цветом).
Составим таблицу 2:
3 строка: элементы 3-й строки из табл.1 разделили на ключевой элемент=3.
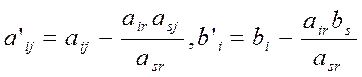
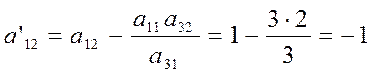
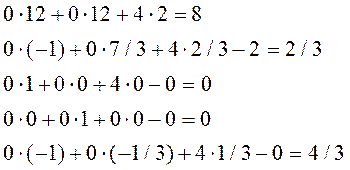
Получилось, что в индексной строке все элементы неотрицательны, значит, задача решена. Базисный план X2=(2,0,12,12,0), для которого f(X2)=8 – есть максимальное значение целевой функции. Значит, X2=(2,0,12,12,0) является оптимальным планом основной задачи (IV)-(VI). Обозначим его X2*=(2,0,12,12,0), тогда f(X2*)=8- максимальное значение целевой функции (VI).
Отбросив значение дополнительных переменных, получим:
Ответ: оптимальный план X*=(2,0) общей задачи (I)-(III), а значение целевой функции останется прежним f(X*)=8.
Таким образом, для того, чтобы получить максимальную прибыль, равную 8 ед., следует использовать 2ед. ресурсов I вида. Значения дополнительных неизвестных x3*=x4*=12 и x5*=0 показывают, что ресурсы I, II видов используются не полностью, а III вида – полностью.
Общая задача (I)-(III) содержит 2 неизвестных, поэтому может быть решена графически.
Введем систему декартовых координат на плоскости x1Ox2 и построим множество планов задача (I)-(III). Каждое линейное неравенство системы определяет полуплоскость по одну сторону от граничной прямой, заданной соответствующим равенством. Множество планов задачи есть пересечение полуплоскостей, представляющих собой выпуклый многоугольник.
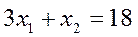
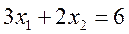
Конспект «Построение математической модели»
МАОУ ООШ п. Мельниково
Построение математической модели как одно из средств обучения школьников решению текстовых задач
Типовой проект работы над задачей включает следующие друг за другом этапы решения задачи:
анализ текста задачи, краткая запись;
поиск способа решения задачи, составление плана ее решения;
решение задачи и его запись; проверка решения задачи;
выбор и запись ответа;
анализ решения задачи, возможные обобщения.
Коротко остановимся на каждом этапе типового проекта.
От качества анализа текста задачи зависит и поиск ее решения. Не надо спешить начинать решать задачу. Необходимо дать время учащимся познакомиться с текстом задачи, внимательно его прочитать. Часто ученики не могут решить задачу еще и потому, что они не понимают условия задачи.
Работу над текстом задачи, в зависимости от уровня обученности учащихся, может проводить учитель; работа может проводиться учителем с привлечением учащихся; учитель может организовать работу в парах; учащиеся могут самостоятельно поработать над текстом задачи.
Анализ текста задачи предполагает: разбиение текста на условие и требование; разбиение условия и требования на элементарные предложения; определение роли и значимости каждого из условий.
При анализе условия целесообразно выяснить:
Какие ситуации рассматриваются в задаче?
Какими величинами они (ситуации) характеризуются?
Что известно о каждой рассматриваемой ситуации?
Эти вопросы первое время формулирует учитель, организуя анализ текста задачи, затем ребята, работая в парах, в группах в процессе решения задач задают эти вопросы друг другу, а уже позже – сами себе во время самостоятельного решения задач.
По итогам анализа содержания выполняется краткая запись. Она может быть выполнена в виде рисунка, схемы, таблицы (нередко ребята одновременно оформляют рисунок и таблицу, схему и таблицу).
Для того чтобы освоить умения по решению текстовых задач, учащиеся должны овладеть некоторыми ориентирами по поиску решения задач. Учитель обязан уметь организовать поиск решения задачи посредством диалога.
Остановимся на алгебраическом способе решения задач. Алгебраический способ – это метод решения задачи путем составления математической модели (уравнения, неравенства) и ее решения. Моделирование позволяет отвлечься от несущественных в данном конкретном случае свойств объекта и отразить какое-то его определенное свойство, что облегчает процесс исследования и, следовательно, решение задачи.
Государственные образовательные стандарты 2-го поколения, с одной стороны, – поддерживают традиции обучения математике, с другой, – расставляют иные акценты и определяют иные приоритеты. Так в условиях образования, ориентированного на развитие мышления у школьников, особое значение в обучении и, прежде всего, при осуществлении решения задач, приобретает овладение действием моделирования, поскольку, как показали исследования, оно способствует формированию обобщённых действий.
Весь процесс, связанный с решением текстовой задачи основан на моделировании:
текст задачи – это знаковая модель реальной ситуации;
сложный текст задачи исследуется с помощью промежуточной, вспомогательной модели (схема, рисунок, таблица, краткая запись);
результаты исследования модели – схемы описываются в виде математической модели, которая является средством для получения ответа на требование задачи;
запись ответа – перевод полученного решения на тот язык, на котором была сформулирована задача.
Все вспомогательные модели (текст, схема, рисунок, таблица, краткая запись, уравнение) являются различными моделями одного и того же объекта. Задачи и различаются тем, что выполнены на разных языках: языке слов, языке образов, языке математических символов.
С этой позиции процесс формирования умения решать задачи можно рассматривать как обучение приемам перевода моделей одного вида к модели другого вида, а моделирование выступает в качестве обобщенного способа решения задачи любого типа.
Текстовая задача – это словесная модель некоторого явления (ситуации, процесса). Чтобы решить такую задачу, надо перевести её на язык математических действий, т. е. построить её математическую модель.
М атематическая модель – это описание какого-либо реального процесса на языке математических понятий, формул и отношений.
В процессе решения задачи чётко выделяют три этапа математического моделирования:
1 этап – это перевод условия задачи на математический язык; при этом выделяются необходимые для решения данные и искомые; математическими способами описываются связи между ними (т.е. происходит кодирование информации – запись с помощью знаковой системы);
2 этап – внутримодельное решение (т. е. выполнение действий, составление и нахождение значения переменных);
3 этап – интерпретация, т. е. перевод полученного решения на тот язык, на котором была сформулирована исходная задача (или же декодирование – восстановление сообщения из последовательности знаковых кодов).
В процессе решения текстовой задачи наибольшую сложность представляет перевод текста с естественного языка на математический, т. е. первый этап математического моделирования.
Чтобы облегчить эту процедуру, ребятам и необходимо строить вспомогательные модели-схемы, таблицы и др. Тогда процесс решения задачи можно рассматривать как переход от одной модели к другой: от словесной модели реальной ситуации, представленной в задаче, к вспомогательной (схемы, таблицы, рисунки), от неё – к математической, на которой и происходит решение задачи.
Единых требований к оформлению решения задач нет. Однако нужно
следить за тем, чтобы запись решения отвечала требованиям к решению задач: решение и ответ задачи должны быть правильными; решение должно содержать всю цепочку обоснованных рассуждений, приведших к результату; запись решений должна быть корректной.
Проверка решения задачи может быть выполнена следующими способами: прикидка; соотнесение результата с условием задачи; решение задачи другим способом; составление обратной задачи.
Приведем примеры организации учебной деятельности учащихся по решению задач алгебраическим способом (путем составления математической модели).
Задача 1(5 класс): В первый день в овощном магазине продали на 3,78 т овощей больше, чем во второй день. Сколько овощей продали в каждый из этих дней, если в первый день продали в 4 раза больше, чем во второй?
К этому моменту ребята уже владеют простейшими умениями работы с текстовой задачей, они могут выделить в тексте задачи условие и требование.
Предлагаем вашему вниманию вопросы (эти вопросы первое время формулирует учитель; затем ребята, работая в парах, в группах в процессе решения задач задают эти вопросы друг другу; а уже позже – сами себе во время самостоятельного решения задач), которые формулируются с целью анализа текста задачи.
(а впоследствии, вопросы учащегося сам ому себе)
Предполагаемые ответы у
Какой жизненный процесс описан в задаче?ащихся
Это задача о продаже овощей в магазине
Какими основными величинами характеризуется этот процесс?
Количество овощей в первый день (А), количество овощей во второй день (В)
Каким соотношением (формуло
) связаны эти величины?
А>В на С, А> B в n раз
Какие ситуации описаны в задаче?
1 ситуация: в первый день продали в 4 раза больше, чем во второй;
2 ситуация: в первый же день продали на 3,78т больше, чем во второй день.
Перечисляют все, что известно о величинах и предлагают составить краткую запись
I 

Рассмотрим вопросы, стимулирующие поиск решения: Как вы думаете, какую величину удобнее обозначить за х в этой задаче? Что через нее можно выразить? А достаточно ли здесь условия для решения задачи?
Приведем решение данной задачи через описание этапов моделирования, которые должны быть освоены учащимися основной школы.
1 этап (перевод задачи на математический язык): Пусть х т овощей продали во второй день, тогда 4х т овощей было продано в первый день.
Так как в первый день было продано на 3,78 т овощей больше, чем во второй, то составим уравнение: 4х-х=3,78
2 этап (работа с математической моделью): Решим уравнение:
3 
Учителю важно понимать, что решение учащимися задачи является не самоцелью, а является средством его развития и обучения. Поэтому необходимо организовывать обсуждение (выделение и анализ) проделанных действий и их недостатков, других способов решения, сущности и выявления условий возможности применения тех приемов, которые были использованы для работы над этой задачей.
Задача 2 (6класс): Одна скважина на 3,4 м глубже другой. Если глубину первой скважины увеличить на 21,6 м, а второй – в 3 раза, то обе скважины будут иметь одинаковую глубину. Найдите глубину каждой скважины.
Предлагаем вашему вниманию вопросы (эти вопросы первое время формулирует учитель; затем ребята, работая в парах, в группах в процессе решения задач задают эти вопросы друг другу; а уже позже – сами себе во время самостоятельного решения задач), которые формулируются с целью анализа текста задачи.
(а впоследствии, вопросы учащегося сам ому себе)
Предполагаемые ответы учащихся
Какой жизненный процесс описан в задаче?
Это задача о двух скважинах
Какими основными величинами характеризуется этот процесс?
Глубина 1 скважины (А), глубина второй скважины (В)
формулой) связаны эти величины?
Какие ситуации описаны в задаче?
1 ситуация: 2 скважины имеют первоначальную глубину;
2 ситуация: глубину каждой скважины изменили.
Перечисляют все, что известно о величинах и предлагают составить краткую запись
В процессе работы с текстом задачи ученик не может непосредственно исследовать описанную ситуацию, но полученные результаты анализа текста можно использовать для дальнейшего понимания процесса, описанного в задаче. Для этого их нужно как-то зафиксировать. Надо найти удобную, более компактную, чем словесное описание форму представления содержания и в то же время достаточно наглядную. Такой формой является вспомогательная модель задачи – рисунок, схема, таблица, чертеж, диаграмма и др., позволяющая продемонстрировать отношения, взаимосвязь между данными и искомыми.
Представим краткую запись в виде таблицы (схемы, вспомогательной модели):
Так как вспомогательная модель – это своеобразная копия задачи, на ней должны быть представлены все ее объекты, все отношения между ними, указаны требования. Для проверки правильности построения вспомогательной модели задачи можно задать следующие вопросы: все ли объекты задачи и их величины показаны на модели? все отношения между ними отражены? все ли числовые данные приведены? обозначен ли вопрос?
Предлагаем вопросы, стимулирующие поиск решения: Как вы думаете, какую величину удобнее обозначить за х в этой задаче? Что через нее можно выразить? А достаточно ли здесь условия для решения задачи?
После того, как ответы на эти вопросы будут получены, таблица может выглядеть так:
1 этап (перевод задачи на математический язык): Пусть х м глубина 2 скважины, тогда (х+3,4) м глубина 1 скважины. После изменений (х+25) м стала глубина 1 скважина, 3х м – глубина 2 скважины.
Так как после изменений глубины скважин равны, то составим уравнение: х+25=3х.
2 этап (работа с математической моделью): Решим уравнение:
3 этап (перевод результата 2 этапа на язык задачи): Значит 12,5 м была глубина второй скважины; 15,9 м была глубина 1 скважины.
Задача 3 (7 класс): Катер шел по течению реки 5 ч, а затем против течения 3 ч. Найдите собственную скорость катера, если известно, что скорость течения реки 3 км/ч, а всего пройдено 126 км.
Перечислим величины, характеризующие процесс движения по реке, и их взаимосвязь, которые ребята в результате совместной работы выделяют при первых встречах с такими задачными ситуациями. Эти ориентиры следует внести в банк ориентиров (это может быть отдельная тетрадь, форзац тетради, съемные стенды для кабинета), помогающих успешно решать текстовые задачи.
v собств. – собственная скорость катера;
Скорость тела при движении по течению реки равна сумме собственной скорости тела и скорости течения реки.




Скорость тела при движении против течения реки равна разности собственной скорости тела и скорости течения реки.


Предлагаем вопросы (эти вопросы первое время формулирует учитель; затем ребята, работая в парах, в группах в процессе решения задач задают эти вопросы друг другу; а уже позже – сами себе во время самостоятельного решения задач), которые формулируются с целью анализа текста задачи.
(а впоследствии, вопросы учащегося сам ому себе)
Предполагаемые ответы учащихся
Какой жизненный процесс описан в задаче?
Это задача о движении катера по течению реки и против течения реки
Какими основными величинами характеризуется этот процесс?
Каким соотношением (формулой) связаны эти величины?
Какие ситуации описаны в задаче?
1 ситуация: движение катера по течению;
2 ситуация: движение катера против течения реки
т все, что известно о величинах и предлагают составить краткую запись Рассмотрим вопросы, стимулирующие поиск решения: Как вы думаете, какую величину удобнее обозначить за х в этой задаче? Что через нее можно выразить? А достаточно ли здесь условия для решения задачи?
Представим краткую запись (вспомогательную модель задачи) в виде таблицы:
Для проверки правильности построения вспомогательной модели задачи рекомендуется задать следующие вопросы: все ли объекты задачи и их величины показаны на модели? все отношения между ними отражены? все ли числовые данные приведены? обозначен ли вопрос?
1 этап (перевод задачи на математический язык): Пусть х км/ч собственная скорость катера, тогда (х+3) км/ч скорость катера по течению реки, (х-3) км/ч скорость катера против течения реки.
Зная время движения и скорость, найдем расстояния, которые прошел катер в каждом направлении 5(х+3) км – по течению, 3(х-3) км – против течения.
Так как всего прошел 126 км, составим уравнение: 5(х+3)+3(х–3)=126.
2 этап (работа с математической моделью): Решим уравнение:
3 этап (перевод результата 2 этапа на язык задачи):
15 км/ч собственная скорость катера.
Задача 4 (8 класс) : Две бригады, работая вместе могут выполнить задание за 8 ч. Превая бригада, работая одна, могла бы выполнить задание на 12 ч быстрее, чем вторая бригада. За сколько часов могла бы выполнить задание первая бригада, если бы она работала одна?
Перечислим величины, характеризующие процесс работы, и их взаимосвязь, которые ребята в результате совместной работы выделяют при первых встречах с такими задачными ситуациями. Эти ориентиры следует внести в банк ориентиров (это может быть отдельная тетрадь, форзац тетради, съемные стенды для кабинета), позволяющих успешно решать текстовые задачи.
n – производительность (объем работы за единицу времени);
Задачи на работу для учащихся более трудны и непонятны, в них, как правило, мало данных. Поэтому можно вместе с учениками провести «параллель» между величинами, характеризующими задачи на работу и задачи на движение. В результате возможно появление таблицы, которая может служить неким ориентиром при поиске способа решения задачи:
Вместе с учениками полезно прийти к выводу о том, что если объем всей работы по условию задачи неизвестен, то его можно обозначить за 1.
Предлагаем вашему вниманию вопросы (эти вопросы первое время формулирует учитель; затем ребята, работая в парах, в группах в процессе решения задач задают эти вопросы друг другу; а уже позже – сами себе во время самостоятельного решения задач), которые формулируются с целью анализа текста задачи.
(а впоследствии, вопросы учащегося сам ому себе)
Предполагаемые ответы учащихся
Какой жизненный процесс описан в задаче?
Это задача о работе, которую могут выполнить две бригады вместе и каждая самостоятельно
Какими основными величинами характеризуется этот процесс?
Каким соотношением (формулой) связаны эти величины?
Какие ситуации описаны в задаче?
1 ситуация: работу выполняют вместе ;
2 ситуация: ту же самую работу выполняет 1 бригада;
3 ситуация: ту же самую работу выполняет 2 бригада
Перечисляют все, что известно о величинах и предлагают составить краткую запись
Представим краткую запись и все введенные обозначения (вспомогательную модель задачи) в виде таблицы:
? 
Для проверки правильности построения вспомогательной модели задачи можно задать следующие вопросы: все ли объекты задачи и их величины показаны на модели? все отношения между ними отражены? все ли числовые данные приведены? обозначен ли вопрос?
1 этап (перевод задачи на математический язык): Обозначим за 1 – весь объем работы или по условию задачи – задание.
Пусть х ч – время работы 1 бригады, тогда (х+12)ч – время работы 2 бригады.






2 этап (работа с математической моделью): Решим уравнение:




3 этап (перевод результата 2 этапа на язык задачи): –8 не удовлетворяет условию задачи (время работы не может быть отрицательным), 12 ч – время работы 1 бригады.
Задача 5 (8-9 класс). На соревнованиях по кольцевой трассе один лыжник проходил круг на 3 минуты быстрее другого и через час обогнал ровно на круг. За сколько минут каждый лыжник проходил круг?
Перечислим величины, характеризующие процесс кругового движения, и их взаимосвязь, которые ребята в результате совместной работы выделяют при первых встречах с такими задачными ситуациями. Эти ориентиры, также как и ориентиры в задачах на движение, на работу, на проценты, на смеси и сплавы, необходимо внести в банк ориентиров (это может быть отдельная тетрадь, форзац тетради, съемные стенды для кабинета), позволяющих успешно решать текстовые задачи.
v – скорость движения;
t – время прохождения одного круга;
n – количество кругов;
l – длина одного круга.


Предлагаем вашему вниманию вопросы (эти вопросы первое время формулирует учитель; затем ребята, работая в парах, в группах в процессе решения задач задают эти вопросы друг другу; а уже позже – сами себе во время самостоятельного решения задач), которые формулируются с целью анализа текста задачи.
(а впоследствии, вопросы учащегося сам ому себе)
Предполагаемые ответы учащихся
Какой жизненный процесс описан в задаче?
Это задача о движении двух лыжников по круговой трассе
Какими основными величинами характеризуется этот процесс?
Время прохождения одного круга, время движения, скорость, длина одного круга, расстояние, количество кругов
Каким соотношением (формулой) связаны эти величины?


Какие ситуации описаны в задаче?
У первого лыжника скорость больше, чем у второго и за 1 час первый лыжник обогнал второго ровно на 1 круг
Что известно о скорости, времени и пути каждого лыжника? Как удобно представить эти данные?
Перечисляют все, что известно о величинах и предлагают составить краткую запись
Полезно вместе с учениками создать некую схему, визуализирующую процесс, описанный в задаче.
Рассмотрим вопросы, стимулирующие поиск решения: Как вы думаете, какую величину удобнее обозначить за х в этой задаче? Что через нее можно выразить? А достаточно ли здесь условия для решения задачи?
1

кругов проходил первый лыжник за час, кругов проходил второй лыжник за час.
Известно, что второй лыжник обогнал первого ровно на один круг. Составим математическую модель данной задачи.
2 этап (работа с математической моделью): Решим уравнение:
3 этап (перевод результата 2 этапа на язык задачи): –15 не удовлетворяют условию задачи. 12 минут – время первого лыжника, 15 минут – время второго лыжника.
Ответ: 12 мин, 15 мин.
Задача 6 (встречается с завидным постоянством и в ОГЭ, и в ЕГЭ): Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
Анализ текста задачи:
(а впоследствии, вопросы учащегося сам ому себе)
Предполагаемые ответы учащихся
Какой жизненный процесс описан в задаче?
Это задача о движении двух автомобилей
Какими основными величинами характеризуется этот процесс?
Скорость, время, расстояние
Каким соотношением (формулой) связаны эти величины?
Какие ситуации описаны в задаче?
1 автомобиль проехал весь путь без остановок с одной и той же скоростью
2 автомобиль половину пути ехал с одной скоростью, а вторую половину с другой, но прибыл в конечный пункт одновременно с первым
Перечисляют все, что известно о величинах и предлагают составить краткую запись
1 этап ( перевод задачи на математический язык):
С учащимися одинаковое время можно обозначить знаком =, а клетки расстояния оставить пустыми, но неоднократно проговорить о том, что первый проехал весь путь, а второй проехал его же – как два участка с разными скоростями.
Рассмотрим вопросы, направляющие на поиск решения: Как вы думаете, какую величину удобнее обозначить за х в этой задаче? Что через нее можно выразить? А достаточно ли здесь условия для решения задачи?
Здесь расстояние или пройденный путь можно обозначить – в менее подготовленном классе за s ; а в более подготовленном за 1.
И в результате дополнить таблицу до следующего вида:
2 этап (работа с математической моделью), а именно решение дробно-рационального уравнения: 


3 этап (перевод результата 2 этапа на язык задачи):
– 24 не удовлетворяет условию задачи, скорость не может быть отрицательной.
Значит, 32 км/ч скорость первого автомобиля.
Задача7 (экономическая, похожая задача была в реальном ЕГЭ-2016): Планируется взять кредит на срок 24 месяца. Условия возврата таковы:
первого числа каждого месяца долг возрастает на р% по сравнению с концом предыдущего месяца;
со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите р.
Предполагается, что если ребята берутся за такую задачу, то они умеют выделить в тексте задачи условия и требования и владеют представлениями о нахождении процентов от числа.
Анализ текста задачи:
1 этап ( перевод задачи на математический язык):
Какой жизненный процесс описан в задаче?
Это задача на проценты, о том, что взяли кредит, который согласно заданным условиям возврата необходимо выплатить
Какими основными величинами х арактеризуется этот процесс?
S 
Каким соотношением (формулой) связаны эти величины?
S 


добавленная за n месяцев
Какие ситуации описаны в задаче?
1ситуация: ежемесячно 1 числа остаток долга возрастает на р%
2 ситуация: ежемесячно необходимо выплачивать проценты и 
Перечисляют все, что известно о величинах и предлагают составить краткую запись
Пусть S – сумма кредита,
р – процент, который начисляют ежемесячно на остаток,
1,3 S – сумма, которую необходимо вернуть (общая сумма выплат после полного погашения кредита).
Необходимо вместе с учащимися прийти к этой формуле.
2 этап (работа с математической моделью): Разделим обе части этого уравнения на положительное число S и решим уравнение
1+0,01р + 0,01 p 


0,01р(1+ 


1+ 



0,01р ∙ 
р= 
3 этап (перевод результата 2 этапа на язык задачи):
2,4% – процент, на который ежемесячно возрастал долг по сравнению с концом предыдущего месяца.
Мы привели лишь некоторый набор задач и показали, как можно организовать учебную деятельность учащихся по обучению решению текстовых задач, работе с текстовой информацией.
Список литературы и других источников по теме
Аналитические материалы по результатам проведения национального исследования качества математического образования в 5 – 7 классах – М.: МЦНМО, 2015. – 187 с.: ил.
Владимирцева С.А. Теория и методика обучения математике: Общая методика. – Барнаул: БГПУ, 2004.