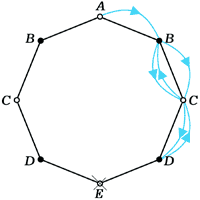
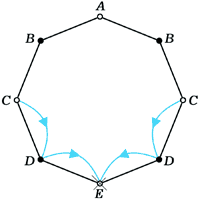
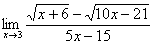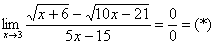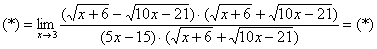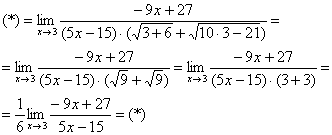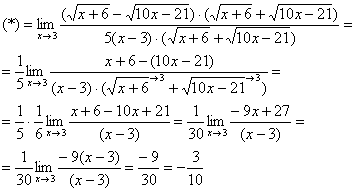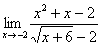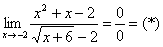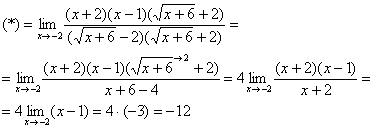Что значит сопряженное выражение

Иррациональность в знаменателе

Если дробь содержит корень в знаменателе, то мы говорим об иррациональности в знаменателе дроби. Часто бывает необходимо освободиться от иррациональности в знаменателе дроби. То есть заменить исходную дробь, содержащую иррациональность в знаменателе на тождественно равную ей дробь, которая иррациональность не содержит. Как это сделать?

Общее правило такое: нужно числитель и знаменатель дроби умножить на выражение, сопряженное знаменателю дроби.

Выражение А называется сопряженным иррациональному выражению В, если произведение АВ не содержит знака корня, то есть произведение АВ является рациональным числом.

Рассмотрим примеры сопряженных выражений.

1. Иррациональное выражение В содержит квадратный корень.

Возможны два случая:

a) . В этом случае :

Например, чтобы исключить иррациональность из знаменателя в дроби , нужно числитель и знаменатель дроби умножить на , получим

б) , =0;

b>=0, a<>b»/>

В этом случае сопряженным выражением будет дополняющее до разности квадратов:

Для выражения сопряженным будет :

Соответственно, для выражения сопряженным будет :

Например, исключим иррациональность из знаменателя дроби

Для этого умножим числитель и знаменатель дроби на выражение, сопряженное знаменателю, то есть на

Получим:

2. Иррациональное выражение В содержит корень n-й степени:

В этом случае сопряженное выражение :

Пример: исключим иррациональность из знаменателя дроби

Умножим числитель и знаменатель дроби на выражение . Получим:

3. Иррациональное выражение В является одним из множителей в разложении на множители разности или суммы кубов. В этом случае сопряженным ему выражением будет второй множитель:

Исключим иррациональность из знаменателя дроби:

Рассмотрим пример упрощения выражения, содержащего иррациональность в знаменателе дроби.

Найти значение выражения:

Внимание! Если нужно упростить выражение, содержащее иррациональность в знаменателе, то первым делом исключаем иррациональность из знаменателя, даже если кажется, что без этого можно обойтись.

Итак, исключим иррациональность из знаменателя первой и второй дроби:

Подставим полученные выражения в исходное:

Источник

Метод умножения числителя и знаменателя на сопряженное выражение

Продолжаем рассматривать неопределенность вида

Следующий тип пределов похож на предыдущий тип. Единственное, что помимо многочленов, у нас добавятся корни.

Найти предел

Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела.Данное действие обычно проводится мысленно или на черновике.

Получена неопределенность вида 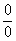, которую нужно устранять.

Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по-возможности, избавляться. Зачем? А без них жизнь проще.

Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности 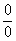используют метод умножения числителя и знаменателя на сопряженное выражение.

Вспоминаем нашу нетленную формулу разности квадратов: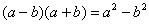
И смотрим на наш предел: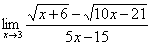
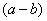
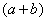
Что можно сказать? у нас в числителе уже есть. Теперь для применения формулы осталось организовать (которое в и называется сопряженным выражением).

Умножаем числитель на сопряженное выражение:

Обратите внимание, что под корнями при этой операции мы ничего не трогаем.

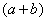
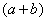
Хорошо, мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на :

То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.

Умножили. Теперь самое время применить вверху формулу :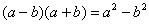

Неопределенность 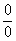не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:

Число, как уже отмечалось ранее, лучше вынести за значок предела.

Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше.

Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:

Умножим числитель и знаменатель на сопряженное выражение.

Найти предел

Сначала попробуйте решить его самостоятельно.

Окончательное решение примера может выглядеть так:

Разложим числитель на множители:

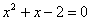
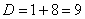
Умножим числитель и знаменатель на сопряженное выражение

Спасибо за внимание.

Помимо рассмотренных типов пределов на практике часто встречаются так называемые Замечательные пределы, с которыми Вы можете ознакомиться в соответствующей статье.

Источник

Как освободиться от иррациональности в знаменателе: способы, примеры, решения

При изучении преобразований иррационального выражения очень важным является вопрос о том, как освободиться от иррациональности в знаменателе дроби. Целью этой статьи является объяснение этого действия на конкретных примерах задач. В первом пункте мы рассмотрим основные правила данного преобразования, а во втором – характерные примеры с подробными пояснениями.

Понятие освобождения от иррациональности в знаменателе

Начнем с пояснения, в чем вообще заключается смысл такого преобразования. Для этого вспомним следующие положения.

Освободиться от иррациональности в знаменателе дроби – значит преобразовать ее, заменив на тождественно равную дробь, в знаменателе которой не содержится корней и степеней.

После формулировки определения мы можем переходить непосредственно к изучению последовательности действий, которые нужно выполнить для такого преобразования.

Основные действия для избавления от иррациональности в знаменателе дроби

Для освобождения от корней нужно провести два последовательных преобразования дроби: умножить обе части дроби на число, отличное от нуля, а затем преобразовать выражение, получившееся в знаменателе. Рассмотрим основные случаи.

Иногда преобразования, которые нужно выполнить, бывают довольно специфическими. Разберем несколько наглядных примеров.

Как преобразовать выражение в знаменателе дроби

Как мы уже говорили, проще всего выполнить преобразование знаменателя.

Условие: освободите дробь 1 2 · 18 + 50 от иррациональности в знаменателе.

Решение

Запишем ход всего решения без комментариев:

1 2 · 18 + 50 = 1 2 · 18 + 2 · 50 = = 1 2 · 18 + 2 · 50 = 1 36 + 100 = 1 6 + 10 = 1 16

Решение

Избавление от иррациональности методом умножения на корень

Решение

x 3 = x · 3 3 · 3 = x · 3 3 2 = x · 3 3

Если же в знаменателе исходной дроби имеются выражения вида A n m или A m n (при условии натуральных m и n ), нам нужно выбрать такой множитель, чтобы получившееся выражение можно было преобразовать в A n n · k или A n · k n (при натуральном k ). После этого избавиться от иррациональности будет несложно. Разберем такой пример.

Решение

7 6 3 5 = 7 · 6 2 5 6 3 5 · 6 2 5 = 7 · 6 2 5 6 3 5 · 6 2 = 7 · 6 2 5 6 5 5 = = 7 · 6 2 5 6 = 7 · 36 5 6

x x 2 + 1 4 15 = x · x 2 + 1 4 x 2 + 1 4 15 · x 2 + 1 4 = = x · x 2 + 1 4 x 2 + 1 4 16 = x · x 2 + 1 4 x 2 + 1 4 4 4 = x · x 2 + 1 4 x 2 + 1 4

Избавление от иррациональности методом умножения на сопряженное выражение

Решение

Возможно также перед умножением выполнить преобразование: если мы вынесем из знаменателя сначала минус, считать будет удобнее:

Важно обратить внимание на то, чтобы выражение, полученное в итоге умножения, не обращалось в 0 ни при каких переменных из области допустимых значений для данного выражения.

Решение

x x + 4 = 16 16 + 4 = 16 4 + 4 = 2

Преобразование дробей с иррациональностью в знаменателе с использованием формул суммы и разности кубов

Решение

Последовательное применение различных способов преобразования

Часто на практике встречаются более сложные примеры, когда мы не можем освободиться от иррациональности в знаменателе с помощью всего одного метода. Для них нужно последовательно выполнять несколько преобразований или подбирать нестандартные решения. Возьмем одну такую задачу.

Решение

Выполним умножение обеих частей исходной дроби на сопряженное выражение 7 4 + 2 4 с ненулевым значением. Получим следующее:

А теперь применим тот же способ еще раз:

Источник

Что значит сопряженное выражение

Иррациональными называют неравенства, в которых переменные входят под знаком корня. Так как корень чётной степени существует только у неотрицательных чисел, то при решении неравенств, содержащих такое выражение, прежде всего удобно найти ОДЗ.

Решите неравенство `sqrt(x + 3) > x + 1`.

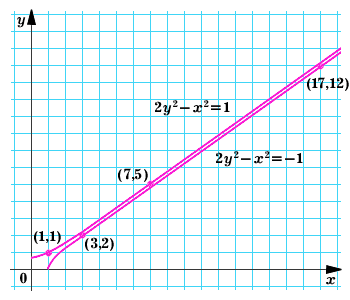
Это неравенство можно решить несколькими способами. Решим его графически.

Рис. 1

Построим графики функций `y = sqrt(x + 3)`, `y = x + 1` и посмотрим, где первый график расположен выше второго. Для нахождения решения останется решить только уравнение `sqrt(x + 3) = x + 1` (и не надо рассматривать случаи разных знаков для `x + 1`!).

`[- 3; 1)`.

Сначала приведём уже выведенные в 10-ом классе условия равносильности для уравнений (в частности, для того, чтобы была понятна приведённая уже здесь нумерация условий равносильности для корней `(`УР К`)`):

ПУНКТ 1. НЕРАВЕНСТВА ВИДА `sqrt(f(x)) >= g(x)` и `sqrt(f(x))

1. Если `x` является решением неравенства `sqrt(f(x)) >= g(x)`, то `f(x) >= 0` и `sqrt(f(x))` существует. При этом неравенство заведомо выполнено при `g(x) = 0`, то возведение в квадрат обеих частей неравенства приводит к равносильному неравенству `f^2 (x) >= g^2 (x)`.

2. Пусть теперь `x` является решением совокупности неравенств

$$\left[\begin\left\<\beging\left(x\right) = 0`, то существует `sqrt(f(x))` и заведомо выполнено неравенство `sqrt(f(x)) >= g(x)`:

б) если `g(x) >= 0` и

Можно ОДЗ неравенства найти отдельно, тогда условие равносильности примет вид:

Первый способ

Воспользуемся (УР К5):

`3sqrt(3x^2-8x-3)>1-2x iff`$$\left[\begin\left\<\begin1-2x \left(1-2x\right)^2\end\right.\end\right.\Leftrightarrow$$

Второй способ

Можно оформить решение неравенства и несколько по – другому. Найдём сначала ОДЗ:

`iff x in (- oo; (34-30sqrt2 )/(23)) uu ((34+30 sqrt2)/(23); + oo)`.

Заметим, что ОДЗ в этом случае выполнилось автоматически.

то `f(x) >= 0`, `g(x) >= 0`, `sqrt(f(x))` и `sqrt(g(x))` существуют.

Рассмотрим довольно часто встречающееся неравенство вида

Теперь используем эти свойства для решения довольно сложных неравенств вида

Сейчас мы покажем, что можно обойтись, хотя и двумя случаями, но без корней.

2. Если же `g(x) >= 0`, то разность может менять знак в зависимости от значений `x`, но сумма `sqrt(f(x)) + g(x)` всегда неотрицательна в ОДЗ, и умножение обеих частей неравенства на это сопряжённое выражение приводит к равносильному неравенству, т. е. в этом случае

Для неравенства другого знака меняется лишь знак неравенства. Объединив оба условия, получаем новое замечательное условие равносильности в ОДЗ:

Найденные в результате исследования совокупности (УР К9) решения следует сравнить с ОДЗ.

Решите неравенство `(4x+15-4x^2)/(sqrt(4x+15) +2x) >=0`.

Теперь в ОДЗ преобразуем неравенство:

Попробуем решить эту систему графически. Из графика на рисунке 2 видно, что неравенство выполнено от точки `x=-(15)/4` до абсциссы точки пересечения кривой `y=sqrt(4x+15)` и прямой `y=2x`.

Рис. 2

Найдём эту абсциссу:

Заметим, что для решения уравнения мы возводили обе части в квадрат, а, значит, одновременно с нашим решили «чужое» уравнение:

А в нашей системе решение этого уравнения `x=-3/2` как раз нам надо исключить. Главное в том, что для решения всей системы, оказалось достаточно решить единственное уравнение

Источник

Что значит сопряженное выражение

Читателю, вероятно, известны на первый взгляд трудные геометрические задачи, которые мгновенно решаются, если заменить одну данную точку другой, симметричной ей относительно прямой. Соображения симметрии очень важны и в алгебре.

В этой статье мы рассмотрим ряд ситуаций, в которых число вида полезно заменить сопряжённым Мы увидим, как этот простой приём — замена знака перед радикалом — помогает в решении разнообразных задач алгебры и анализа — от нехитрых оценок и преобразований до трудных олимпиадных задач и замысловатых придумок составителей конкурсных экзаменов.

Большинство наших примеров может служить первым знакомством с глубокими математическими теориями мы указываем статьи и книги для продолжения знакомства). Среди задач, включённых в статью, две — из Задачника «Кванта» и несколько — из писем читателей, уже испытавших удовольствие от трюков с радикалами и желающих поделиться им с другими.

Пары сопряжённых чисел появляются вполне естественным образом, когда мы решаем квадратное уравнение, а корень из дискриминанта не извлекается: скажем, уравнение имеет пару «сопряжённых» корней:

К этому мы ещё вернёмся, а начнём с примеров другого рода: займёмся «перебросками».

Если в книжке указан ответ к задаче а у вас получилось — не спешите искать ошибку в решении: ответ правильный — эти числа равны, потому что

Вот несколько характерных примеров, где полезно перенести «иррациональность» из числителя в знаменатель или наоборот.

Эта сумма мгновенно «сворачивается», если переписать её так:

По выражению из статьи [1] «остаются крайние» (см. также [5]).

2. Доказать, что для любых натуральных m и n

Подобный факт мы использовали недавно при решении трудной задачи

В самом деле, всегда

поскольку число — целое и отлично от 0 (равенство невозможно — подумайте, почему!). Если бы выполнялось неравенство, противоположное (1), то должно было бы быть и

n ( m + n √ 2 ) n ( 2 n √ 2 + 1 Но из (2) и (3) следует (1). Значит, наше предположение неверно, то есть (1) выполнено. Оно лишь немного сильнее, чем неравенство (1), поскольку π = 0,3183. > 0,3178. = 1 зато выглядит гораздо эффектнее. Помню как в мою бытность студентом на лекциях по алгебре наш профессор говорил: «Корень из это, примерно, 1,73; корень из 1,41. Поэтому их сумма равна. (следовала пауза, необходимая для сложения этих чисел 3,14. (он поворачивался к аудитории и сразу несколько человек с удовлетворением заключал профессор, выписывая окончательное «равенство»: 🙂 ] 3. Найдите предел последовательности Преобразуем a n так: Теперь ясно, что a n возрастает и стремится к В противоположность предыдущему примеру здесь мы имеем дело с хорошим приближением: 4 (M532). Даны две последовательности и Докажите, что В разности появляется «тройная иррациональность»; к таким иррациональностям мы ещё вернёмся (см. задачу 8), но пока мы будем рассматривать как одно целое. Заметим, что величина очевидно, заключена между и поскольку Итак, мы уже получили — левое неравенство Кроме того, число дающее при делении на 4 в остатке 2, не может быть полным квадратом (проверьте!), поэтому квадрат целого числа не больше из неравенств Теперь осталось оценить разность сверху. Посмотрите, как здесь дважды работает переброска «сопряжённого» числа в знаменатель: √ 4 n +2 – √ n – √ n +1 = 2 n + 1 – 2√ n ( n + 1) √ 4 n + 2 + √ n + √ n + 1 = = 1 (√ 4 n + 2 + √ n + √ n + 1 )(2 n + 1 + 2√ n ( n + 1) ) ≤ ≤ 1 (2√ n + √ n + √ n )(2 n + 2 n ) = 1 Заметим, что и эта оценка очень точная. Но убедиться в этом (и вообще исследовать поведение функции с многими радикалами) лучше уже не с помощью алгебраических преобразований, а средствами анализа — заменить переменную n на и воспользоваться формулой Тейлора Мы уже говорили о пользе симметрии в геометрических задачах. Своего рода симметрией в алгебре является замена плюса на минус. Так, если какое-либо выражение от равно и мы всюду в этом выражении заменим на то естественно ожидать, что новое выражение окажется равным сопряженному числу Мы будем пользоваться таким очевидным частным случаем этого свойства ( a и b — рациональны, — нет): 5. Доказать, что уравнение не имеет решений в рациональных числах x, y, z, t. Можно, конечно, найти отдельно сумму членов левой части, не содержащих (она должна быть равна 2), и отдельно — коэффициент при (он должен равняться 1). Но что делать с полученной громоздкой системой неясно. Вместо этого воспользуемся (4) и заменим плюс перед на минус! Слева стоит неотрицательное число, справа — отрицательное. 6. Доказать, что существует бесконечно много пар натуральных чисел, для которых x 2 отличается от 2 y 2 Несколько таких пар с небольшими легко найти подбором: это (1; 1), (3; 2), (7; 5), (рис. 1). Как продолжить этот набор? Можно ли записать общую формулу для этих решений? Рис. 1. Проходят ли эти гиперболы через бесконечное число узлов клетчатой бумаги? Найти ответы на эти вопросы нам поможет число Закономерность, позволяющая получать всё новые и новые решения указана в таблице: n (1 + √ 2 ) n x n y n x n 2 – 2 y n 2 (1 – √ 2 ) n 1 1 + √ 2 1 1 1 – 2 = –1 1 – √ 2 2 3 + 2√ 2 3 2 9 – 8 = 1 3 – 2√ 2 3 7 + 5√ 2 7 5 49 – 50 = –1 7 – 5√ 2 4 17 + 12√ 2 17 12 289 – 288 = 1 17 – 12√ 2 5 41 + 29√ 2 41 29 1681 – 1682 = –1 41 – 29√ 2 . . . . . . Какой будет шестая строчка? будут давать нужную пару. Доказать это поможет колонка таблицы из сопряжённых чисел (мы снова Перемножив два последних равенства, получим и интересующее нас выражение попеременно равно то 1, то Складывая и вычитая эти же два равенства, мы получим явное выражение для x n и y n : Освободитесь от иррациональности в знаменателе: Источник ← Что значит сопряженно отраженные способы действия с предметом Что значит сопряженное устройство → Вам также понравится Чем обезболить кишечные колики 13.04.202213.04.2022 admin 0 Что случилось с гимнастом рязановым 18.04.202222.04.2022 admin 0 Что значит распаячная коробка 16.04.202218.04.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев. x n = (1 + √ 2 ) n + (1 – √ 2 ) n 2 , y n = (1 + √ 2 ) n – (1 – √ 2 ) n Можно ли в решении этой задачи про целые числа обойтись без иррациональных чисел и Теперь, зная ответ, мы можем легко выразить через предыдущую пару из ( x n + y n √ 2 )(1 + √ 2 ) вытекает До этого рекуррентного соотношения можно было, видимо, догадаться по нескольким первым решениям, а потом проверить, что Рекуррентные соотношения типа (6) возникают не только в теории чисел, но и в разных задачах анализа, теории вероятностей. Вот характерный пример комбинаторной задачи такого типа (она предлагалась на последней международной олимпиаде в Лондоне): 7 (М595). В вершине A правильного восьмиугольника сидит лягушка. Из любой вершины восьмиугольника, кроме вершины E, противоположной A, она может прыгнуть в любую из двух соседних вершин. Попав в E, лягушка останавливается и остаётся там. Найти количество e m различных способов, которыми лягушка может попасть из вершины A в E ровно за m прыжков. А интересующее нас число e 2 n равно, очевидно, а) c 1 = 1 б) a 1 = 2 в) a n +1 = 2 a n + 2 c n г) c n +1 = a n + 2 c n д) e 2 n = 2 c n –1 Из A в C за два прыжка можно попасть только одним способом: Из A в A за два прыжка можно попасть двумя способами: В A можно попасть из C двумя способами и из A двумя способами: В C можно попасть из A одним способом и из C — двумя: В E можно попасть из C двумя способами: Рис. 2. а) б) в) г) д) a n +1 + c n +1 √ 2 = ( a n + c n √ 2 )(2 + √ 2 ) (8) и — как вы уже, конечно, догадались — ещё так: a n +1 – c n +1 √ 2 = ( a n – c n √ 2 )(2 – √ 2 ). (9) Отсюда по индукции, пользуясь (7), получаем: Докажите, что последовательность содержит бесконечно много квадратов целых чисел. Составьте квадратное уравнение с целыми коэффициентами, один из корней которого Составьте уравнение 4-й степени с корнями и решите его, как биквадратное уравнение. Сравнивая ответ с данными корнями, докажите популярные формулы для двойных радикалов: c n = (2 + √ 2 ) n – (2 – √ 2 ) n а так как получаем окончательно Докажите, что функция — нечётная, и постройте её график. а) Докажите, что для любого натурального n б) Докажите, что последовательность убывает и стремится к пределу. а) Докажите, что последовательность сходится, и найдите её предел. б) Каковы первые 100 десятичных знаков после запятой в записи числа 2 + √ 2 + p e 2 n = (2 + √ 2 ) n –1 – (2 – √ 2 ) n –1 Задача решена. Неясно только, как в этой задаче (и в предыдущей задаче 6) можно было додуматься до формул, содержащих — ведь в задаче речь идёт о целых числах! (Для участников олимпиады и читателей «Кванта» задача 7 была облегчена тем, что в формулировке указывался ответ — «Квант», 1979, № 11, М595 ). Однако «сопряжённые числа» возникли бы совершенно автоматически, если бы мы владели началами линейной алгебры (см. [12]), и применили стандартные правила этой науки к решению уравнений (7). Эти правила предлагают сначала выяснить, какие геометрические прогрессии удовлетворяют данному рекуррентному соотношению. Значения, для которых такие прогрессии существуют, — они называются характеристическими значениями или собственными числами — определяются из некоторого уравнения (оно тоже называется характеристическим ). Для (7) характеристическое уравнение имеет вид его корни — как раз и Зная эти корни, любое решение рекуррентного соотношения мы можем получить как «линейную комбинацию» соответствующих геометрических прогрессий ([11]). «Начальное условие» (в нашем случае определяет нужное нам решение однозначно. Неудивительно, что даже самые простые рекуррентные целочисленные последовательности, для которых характеристическое уравнение — квадратное с целыми коэффициентами (примеры — те же (6) и (7) или последовательность Фибоначчи 1, 1, 2, 3, 5, см. [9], [10]), выражаются, как функции номера, с помощью «сопряжённых» квадратичных иррациональностей. Интересное продолжение этого факта мы увидим в следующей задаче с бо́льшим числом «сопряжённых» иррациональностей. Конечно, мы здесь можем выразить через ( q n ; r n ; s n ; t n ), пользуясь тем, что Нетрудно сообразить, каковы будут другие. Рассмотрим вместе с данным числом ещё три «сопряжённых»: Докажите, что при всех положительных x Постройте график функции и докажите, что при q n = λ 1 n + λ 2 n + λ 3 n + λ 4 n 4 , s n = λ 1 n + λ 2 n – λ 3 n – λ 4 n 4√ 3 , r n = λ 1 n – λ 2 n + λ 3 n – λ 4 n 4√ 2 , t n = λ 1 n – λ 2 n – λ 3 n + λ 4 n Теперь заметим, что Поэтому 1 + (λ 2 /λ 1 ) n + (λ 3 /λ 1 ) n + (λ 4 /λ 1 ) n · 1 Аналогично найдём, что Мы говорили выше, что сопряжённые числа возникают часто как корни квадратного уравнения с целыми коэффициентами. В связи с последней задачей возникает такое желание: 9. Написать уравнение с целыми коэффициентами, один из корней которого равен после преобразований получаем Именно такое уравнение получилось бы в качестве характеристического, если бы мы применили упомянутую мелким шрифтом в конце предыдущего раздела общую теорию к исследованию линейного преобразования в предыдущей задаче. Заметим, кроме того, что мы на самом деле получили уравнение наименьшей степени (с целыми коэффициентами) с корнем Попробуйте это доказать! Мы разобрали несколько примеров, в которых затрагивались пограничные вопросы алгебры, математического анализа и теории чисел. (Каждому направлению, которое мы наметили, можно было бы посвятить более подробную статью в «Кванте»!) В заключение покажем ещё, как можно смотреть на основных героев статьи — «сопряжённые числа» — с чисто алгебраической точки зрения. и их «взаимодействие» устроено так же, как во множестве самосовмещений прямоугольника. Мы закончим эту статью набором задач, в основном продолжающих уже затронутые темы, но требующих иногда и новых соображений, и обещанным списком литературы. Что больше: или 2. √ 2 = 1 + 1 . 2 + 1 √ 2 + 1 Докажите, что уравнения имеют бесконечное множество решений в целых числах. 6. 7. 8. 9. = β 1/2 n + β –1/2 n . 12. 13. 14. 2 √ ( A 2 > B > 0, A > 0). 15.