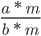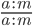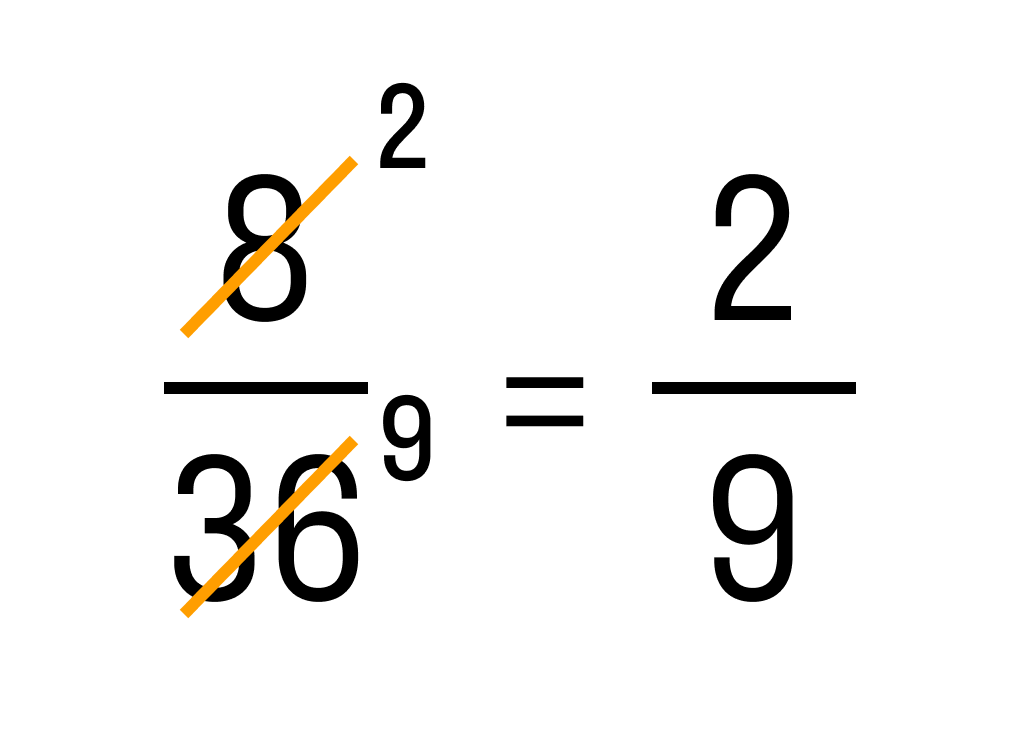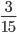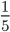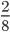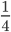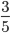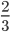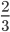Что значит сокращение дробей

Как сокращать дроби: простые примеры с подробными решениями

Содержание:

В этой статье коротко предоставим информацию о том, как сокращать дроби. Сначала приведем немного теоретической части, а затем подкрепим ее решением практических задач.

Что означает сократить дробь

Как сокращаются дроби

Как привести дробь к несократимому виду

Обычно алгебраическое решение любой задачи по сокращению дробей сводится к получению равной дроби, но в несокращаемом виде. Чтобы получить несократимую дробь, ее делят на определенное число, которое называется наибольший общий делитель (сокращенно НОД):

Практически рассмотрим, используя дробь \frac < 6 > < 12 >. Ее можно сократить на НОД, который равняется 6. Тогда 6 : 6 = 1 и 12 : 6 = 2. Следовательно:

Последняя дробь является несократимой.

Следует обратить внимание, что в большинстве случаев если требуется выполнить сокращение дробей, то это значит выполнить до получения несократимой дроби.

Как сократить большую дробь

В качестве нового примера возьмем дробь 144192. Сначала найдем наибольший общий делитель для чисел 144 и 192. Для этого можно применить метод разложения на простые множители:

144 : 2 = 72 192 : 2 = 96

72 : 2 = 36 96 : 2 = 48

36 : 2 = 18 48 : 2 = 24

18 : 2 = 9 24 : 2 = 12

Тогда наибольшим общим множителем для данных чисел будет число 48 = 3 ∙ 2 ∙ 2 ∙ 2 ∙ 2.

Разделив исходную дробь на 48 получим несократимую дробь:

Разберем еще один способ, который позволяет сокращать числитель и знаменатель дроби последовательно на делитель, который без труда определяется по простейшим математическим признакам. Если требуется сократить дробь типа 40008 800, то можно сразу же определить, что здесь присутствует общий множитель 100, который можно вынести за скобку:

Далее невооруженным глазом заметно, что оба числа делятся на 2, а результат опять на 2 и т. д. В конечном итоге получаем несократимую дробь \frac < 5 > < 11 >= \frac < 4000 > < 8800 >. Теперь можно сказать, что наибольшим общим делителем для данной дроби было число 800.

В заключении заметим, что если знаменатель дроби представляет собой числитель, возведенный в квадрат, то такая дробь в несокращаемом виде всегда будет представлять собой: 1 – в числителе + число, значившееся числителем до сокращения, в знаменателе:

Источник

Сокращение дробей. Что значит сократить дробь?

Сокращение дробей нужно для того, чтобы привести дробь к более простому виду, например, в ответе полученном в результате решения выражения.

Сокращение дробей, определение и формула.

Что такое сокращение дробей? Что значит сократить дробь?

Определение:
Сокращение дробей – это разделение у дроби числитель и знаменатель на одно и то же положительное число не равное нулю и единице. В итоге сокращения получается дробь с меньшим числителем и знаменателем, равная предыдущей дроби согласно основному свойству рациональных чисел.

Формула сокращения дробей основного свойства рациональных чисел.

Рассмотрим пример:
Сократите дробь \(\frac<9><15>\)

Решение:
Мы можем разложить дробь на простые множители и сократить общие множители.

Ответ: после сокращения получили дробь \(\frac<3><5>\). По основному свойству рациональных чисел первоначальная и получившееся дробь равны.

Как сокращать дроби? Сокращение дроби до несократимого вида.

Чтобы нам получить в результате несократимую дробь, нужно найти наибольший общий делитель (НОД) для числителя и знаменателя дроби.

Есть несколько способов найти НОД мы воспользуемся в примере разложением чисел на простые множители.

Получите несократимую дробь \(\frac<48><136>\).

Решение:
Найдем НОД(48, 136). Распишем числа 48 и 136 на простые множители.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
НОД(48, 136)= 2⋅2⋅2=6

Правило сокращения дроби до несократимого вида.

Пример:
Сократите дробь \(\frac<152><168>\).

Решение:
Найдем НОД(152, 168). Распишем числа 152 и 168 на простые множители.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
НОД(152, 168)= 2⋅2⋅2=6

Ответ: \(\frac<19><21>\) несократимая дробь.

Сокращение неправильной дроби.

Как сократить неправильную дробь?
Правила сокращения дробей для правильных и неправильных дробей одинаковы.

Рассмотрим пример:
Сократите неправильную дробь \(\frac<44><32>\).

Решение:
Распишем на простые множители числитель и знаменатель. А потом общие множители сократим.

Сокращение смешанных дробей.

Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.

Рассмотрим пример:
Сократите смешанную дробь \(2\frac<30><45>\).

Решение:
Решим двумя способами:
Первый способ:
Распишем дробную часть на простые множители, а целую часть не будем трогать.

Второй способ:
Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.

Вопросы по теме:
Можно ли сокращать дроби при сложении или вычитании?
Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:

Решение:
Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.

На какие числа можно сокращать дробь?
Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя. Например, дробь \(\frac<100><150>\).

Распишем на простые множители числа 100 и 150.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50

Получили несократимую дробь \(\frac<2><3>\).

Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь \(\frac<100><150>\) на 2.

Получили сократимую дробь \(\frac<50><75>\).

Какие дроби можно сокращать?
Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь \(\frac<4><8>\). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.

Пример:
Сравните две дроби \(\frac<2><3>\) и \(\frac<8><12>\).

Эти две дроби равны. Рассмотрим подробно дробь \(\frac<8><12>\):

Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.

Пример:
Сократите если возможно следующие дроби: а) \(\frac<90><65>\) б) \(\frac<27><63>\) в) \(\frac<17><100>\) г) \(\frac<100><250>\)

Источник

Сокращение дробей. Что значит сократить дробь?

Сокращение дроби

Правило сокращения

Если и числитель, и знаменатель обыкновенной дроби имеют общий делитель, то их можно поделить на этот делитель, тем самым получив новую дробь, равную исходной. Эта действие называется сокращением дроби.

При этом, если числитель и знаменатель дроби взаимно просты, то она является несократимой.

Чтобы сократить дробь, выполняем следующие действия:

Пример: сократим дробь 27 /₄₅.

Решение В данном случае одним из множителей и числителя, и знаменателя является число 9, на которое и можно сократить дробь.

В сжатом виде сокращение обычно записывается так: числитель и знаменатель зачеркиваем, рядом с ними подписываем частные от их деления на общий делитель, который держим в уме, затем ставим знак равно и пишем получившуюся дробь.

Сокращение может выполняться поэтапно, т.е. делим дробь сначала на один общий делитель, затем – на другой.

Использование НОД

Чтобы за одно действие сразу максимально сократить дробь, требуется найти наибольший общий делитель (НОД) числителя и знаменателя. Затем остается только поделить составные части дроби на найденное значение.

Пример: давайте сократим дробь 564 /₂₄₄₈.

Решение Разложим числитель и знаменатель на простые множители.

И обеих раскладках два раза встречается число 2 и один раз – число 3. Следовательно, НОД (564, 2448) = 2 ⋅ 2 ⋅ 3 = 12.

Таким образом, исходную дробь можно максимально сократить, разделив ее на 12.

Правило сокращения дроби до несократимого вида

Пример: Сократите дробь \(\frac<152><168>\).

Решение: Найдем НОД(152, 168). Распишем числа 152 и 168 на простые множители. 152=2⋅2⋅2⋅19 168=2⋅2⋅2⋅3⋅7 НОД(152, 168)= 2⋅2⋅2=6

Ответ: \(\frac<19><21>\) несократимая дробь.

Видео

Основное свойство дроби

Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится.

Например, рассмотрим дробь . Умножим её числитель и знаменатель на одно и то же число, например на число 2

Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:

Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.

Рассмотрим дробь . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2

Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:

Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.

Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!

Дробь означает деление

Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.

Например, рассмотрим дробь . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:

Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:

Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».

Приведение дробей к несократимому виду

В предыдущем примере мы сократили дробь 624 на 2, в результате чего получили дробь 312. Нетрудно заметить, что эту дробь можно сократить еще. Как правило, целью сокращения дробей является получение в итоге несократимой дроби. Как привести дробь к несократимому виду?

Сложные выражения

Многочлены, стоящие в числителе или знаменателе, имеющие первую степень, сокращать довольно легко. Но часто в задании попадаются степенные выражения. Для того чтобы их упростить, нужно хорошо знать основные формулы и свойства степеней. Заключаются они в следующем:

В заданиях могут встречаться рациональные и простые числа, известные и неизвестные. Решают их таким же образом. Например, нужно сократить дробь со степенями и буквами: ((0,25 ) p +1 * 8 p ) / (2 2p+1 * (0,5) p-1 ) = (0,25 p * 0,25 1 * 8 p ) / (2 2p * 2 1 * 0,5 p :0,5 1 ) = (1 / 4) p * 0,25 * 8 k / 4 p * 4 * 0,5 p = 2 p * 0,25 / 2 p * 4 = 0,25 / 4 = (1/4) / 4 = 1 / 4* 4 = 1/16.

Смотря на этот пример, можно понять важность упрощения дробей. Ведь из задания, практически недоступного для решения, получилось простейшее наглядное выражение. Но при этом может случиться так, что исходная формула будет довольно сложна для предварительного анализа, например, содержать квадратный корень, экспоненту или логарифм. Для таких случаев есть резон использовать специализированные сайты-вычислители.

Свойства дроби

По сути, сократить дробь — значит, её упростить. Можно использовать разный алгоритм, но в любом случае применяется основное свойство отношений. Заключается оно в том, что если делитель или делимое умножить на одно и то же число, то количественное значение в ответе не изменится. Это правило справедливо и при замене операции умножения на деление.

Алгебраически свойство можно записать в виде равенства: (q * c) / (r * c) = q / r. Для объяснения этого правила используется следующее доказательство. Пусть имеется равенство (q * r) * c = (c * r) * q. Оно возможно, так как соответствует закону умножения натуральных чисел. При этом учитывается свойство деления, согласно которому, если число разделить на равное ему значение, то результатом действия будет единица. Например, с / с = 1 или 12к/12k = 1. Последнее правило довольно логичное и интуитивно понятное. Если представить, что есть число вещей, равное x, и их нужно разложить на кучки так, чтобы в каждой оказалось x предметов, то очевидно, что получится лишь одна кучка.

Исходя из этих двух правил, можно утверждать, что выражения q * c / r * c и q : c / r : c равны q / r. То есть эти два выражения равны друг другу. На уроках математики в школе предлагают графическую иллюстрацию основного свойства. Пусть есть квадрат, который набран из девяти других квадратов. Каждый из них, в свою очередь, разделён на четыре части. Можно утверждать, что основная фигура поделена на 9 * 4 = 36 частей.

Если закрасить пять больших квадратов другим цветом, то фактически будет окрашено 20 квадратов меньшего размера (4 * 5). Отмеченная область составляет 5/9 от целого квадрата или 20/36, если считать маленькие фигуры. Но так как окрашенная часть одна, то справедливо будет утверждать о верности равенства 5 / 9 = 20 / 36. Вместо чисел 20 и 36 можно подставить их произведения. В итоге получится выражение: 5 / 9 = 5 * 4 / 9 * 4 = 20 * 4 / 36 * 4 = 20 / 36. Что и следовало доказать.

Свойство дроби используется при поиске наименьшего и наибольшего общего знаменателя, а также позволяет упрощать выражения. Невозможно правильно научиться сокращать дроби, не понимая рассмотренного правила.

Сокращение смешанных дробей

Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.

Рассмотрим пример: Сократите смешанную дробь \(2\frac<30><45>\).

Решение: Решим двумя способами: Первый способ: Распишем дробную часть на простые множители, а целую часть не будем трогать.

Второй способ: Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.

Вопросы по теме: Можно ли сокращать дроби при сложении или вычитании? Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:

Решение: Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.

На какие числа можно сокращать дробь? Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя. Например, дробь \(\frac<100><150>\).

Распишем на простые множители числа 100 и 150. 100=2⋅2⋅5⋅5 150=2⋅5⋅5⋅3 Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50

Получили несократимую дробь \(\frac<2><3>\).

Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь \(\frac<100><150>\) на 2.

Получили сократимую дробь \(\frac<50><75>\).

Какие дроби можно сокращать? Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь \(\frac<4><8>\). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.

Пример: Сравните две дроби \(\frac<2><3>\) и \(\frac<8><12>\).

Эти две дроби равны. Рассмотрим подробно дробь \(\frac<8><12>\):

Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.

Пример: Сократите если возможно следующие дроби: а) \(\frac<90><65>\) б) \(\frac<27><63>\) в) \(\frac<17><100>\) г) \(\frac<100><250>\)

Источник

Сокращение обыкновенных дробей

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Что такое «сокращение дробей»

Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.

Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.

В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:

Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.

С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:

=

=

где a, b, m — натуральные числа.

Графически сокращение дробей обычно записывается вот так:

Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.

Больше наглядных примеров и понятных объяснений — на курсах обучения математике в онлайн-школе Skysmart.

Пример 1. Сократим обыкновенную дробь

Разделим числитель и знаменатель на общий делитель 3.

= =

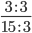
Сокращение выполнено: =

Пример 2. Сократим обыкновенную дробь

Разделим числитель и знаменатель на общий делитель 2.

= =

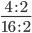
Сокращение выполнено: =

Приведение дробей к несократимому виду

Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.

Так, в результате сокращения в примере 2, мы из дроби получили дробь

Выходит, что дробь выдержит еще одно сокращение и придет к виду

Сокращая дробь, стремитесь в итоге получить несократимую дробь.

Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.

— несократимая дробь, так как по свойствам НОД мы знаем, что:

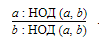
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.

Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.

Пример 3. Приведите обыкновенную дробь к несократимому виду

Найдем НОД числителя и знаменателя. НОД = 12

Найдем частное: 12 : 12 = 1

= =

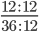
Сокращение выполнено: =

Пример 4. Приведите обыкновенную дробь к несократимому виду

Найдем НОД числителя и знаменателя. НОД = 5

Найдем частное: 15 : 5 = 3

= =

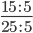
Сокращение выполнено: =

Правило сокращения дробей

Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.

Выполняйте сокращение дробей по следующему алгоритму:

В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.

Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.

Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7

Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.

Пример 5. Сократите дробь

Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5

Мысленно убираем все общие множители и перемножаем оставшиеся.

= =

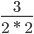
Сокращение выполнено: =

Пример 6. Сократите обыкновенную дробь

Найдем НОД числителя и знаменателя. НОД = 9

= =

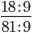
Сокращение выполнено: =

Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.

Пример 6. Сократите дробь:

= = =

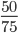
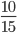
Сокращение выполнено: =

Пример 7. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

168 = 2 * 2 * 2 * 3 * 7

240 = 2 * 2 * 2 * 2 * 3 * 5

Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24

НОД 168 и 240 равен 24

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7

= =

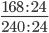
Сокращение выполнено: =

Пример 8. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

360 = 2 * 2 * 2 * 3 * 3 * 5

540 = 2 * 2 * 3 * 3 * 3 * 5

Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180

НОД 360 и 540 равен 180

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2

= =

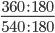
Сокращение выполнено: =

Пример 8. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

420 = 2 * 2 * 3 * 5 * 7

2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7

Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420

НОД 420 и 2520 равен 420

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1

= =

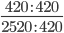
Сокращение выполнено. Дробь приведена к несократимому виду: =

Пример 9. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

1575 = 3 * 3 * 5 * 5 * 7

3450 = 2 * 3 * 5 * 5 * 23

Перемножаем все общие множители между собой 3 * 5 * 5 = 75

НОД 1575 и 3450 равен 72

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21

= =

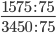
Сокращение выполнено. Дробь приведена к несократимому виду: =

Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.

Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.

Источник