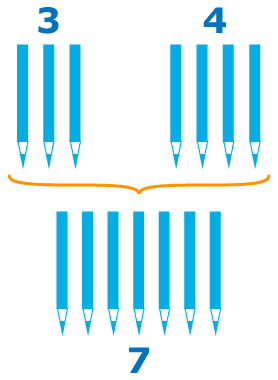
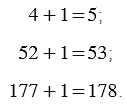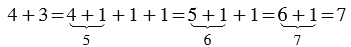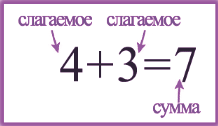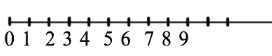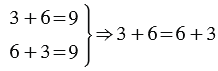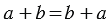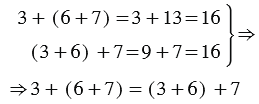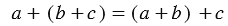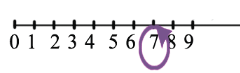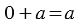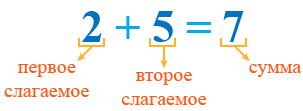Что значит сложить два числа
Сложение натуральных чисел
К нескольким натуральным числам прибавим 1:
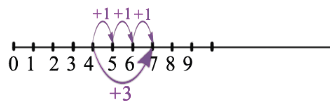
Мы видим, что когда мы прибавляем к натуральному числу 1, получаем следующее за ним натуральное число, т.е. следующее число больше предыдущего на единицу. Теперь к 4 прибавим 3: 4+3: для этого к 4 прибавим 3 раза единицу. Учитывая, что при прибавлении к числу единицы получаем следующее число, получим:
Но мы записываем коротко: 4+3=7.
Числа, которые складываются, называются слагаемыми, число, которое получается в результате сложения, называется суммой.
Сложение чисел на координатном луче
Изобразим координатный луч. Отметим на нем начало координат, единичный отрезок и несколько чисел, следующих друг за другом:
Рассмотрим наш пример: 4+3. Для того чтобы к 4 прибавить 3 на координатном луче, необходимо от точки 4 вправо отложить 3 единичных отрезка:
И мы попадем в точку 7, следовательно 4+3=7.
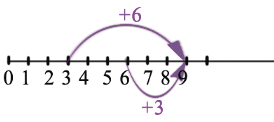
Теперь попробуем отложить на луче, от точки 3 6 единичных отрезков, и от точки 6 3 единичных отрезка, другими словами к 3 прибавим 6 и к 6 прибавим 3 :
Мы видим, что и в первом и во втором случае мы попадаем в одну и ту же точку: 9, следовательно сумма чисел 3 и 6 и 6 и 3 одинакова и равна 9. Это можно записать с помощью равенства:
В этом случае мы меняем местами слагаемые и получаем первое свойство сложения — переместительное свойство :
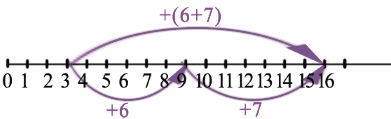
Рассмотрим с помощью координатного луча следующие суммы: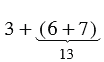 
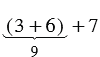
и 
, для этого от точки 3 сначала отложим (6+7) единичных отрезков, а затем от точки 3, отложим сначала 6 единичных отрезков, а затем от получившийся точки отложим еще 7 единичных отрезков:
Заметим, что и в первом и во втором случае мы попадаем в одну точку: 16. Это можно записать равенством:
К натуральному числу можно прибавлять не только натуральное число, но еще и нуль, изобразим на луче прибавление нуля к 7:
Свойства сложения
От перестановки слагаемых сумма не меняется
Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое
Если прибавить к нулю какое-нибудь число, то получится прибавленное число
Сравнение сумм натуральных чисел
Сравним (15+81) и (15+77), для этого рассмотрим слагаемые этих двух сумм: Мы видим, что первые слагаемые у них одинаковые, поэтому переходим к сравнению вторых слагаемых: 81 >77, поэтому (15+81)>(15+77).
Теперь сравним (21+15) и (34+54), для этого опять рассмотрим слагаемые, в данном случае одинаковых у нас нет, но мы видим, что слагаемые первой суммы меньше слагаемых второй суммы, а значит мы можем записать: (21+15) При увеличении слагаемых сумма увеличивается, а при уменьшении уменьшается.
Письменный прием сложения («сложение в столбик»)
Часто при решении задач, нам необходимо складывать многозначные числа, поэтому считать в «уме» или чертить координатный луч не целесообразно, для решения таких задач был придуман письменный прием сложения или «сложение в столбик», который помогает сложение многозначных чисел свести к сложению однозначных чисел, которое мы можем производить легко. Рассмотрим пример:
| 1 | 1 | 1 | |||
| + | 4 | 5 | 8 | 7 | 1 |
| 4 | 3 | 8 | 2 | ||
| 5 | 0 | 2 | 5 | 3 |
Вывод: Если при сложении чисел одного разряда число получается больше или равное 10, то 1 десяток записываем над следующим разрядом, а единицы под рассматриваемым разрядом.
Поделись с друзьями в социальных сетях:
Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
2 + 3 = 5
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
Вывод: два соседних слагаемых можно заменить их суммой.
Поделись с друзьями в социальных сетях:
Свойства сложения и вычитания
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
При этом саму запись (2 + 5) можно тоже назвать суммой.
Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
Свойства вычитания
Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.
Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Разность — это число, которое получается в результате вычитания.
