Что значит скалярная функция

Скалярные функции;

Скалярными называют те функции, которые возвращают одно значение. Эти функции могут принимать множество параметров, выполнять вычисления, но в результате выдают одно значение. Эти функции могут использоваться в любых выражениях, даже участвующих в ограничениях проверки. Значение возвращается функцией с помощью оператора return — эта команда должна завершать скалярную функцию.

В скалярных пользовательских функциях не допускаются операции обновления базы данных, но в то же время они могут работать с локальными временными таблицами. Они не могут возвращать данные BLOB (двоичные большие объекты) таких типов, как text, image и ntext, равно как табличные переменные и курсоры.

Скалярные функции создаются, изменяются и удаляются с помощью тех же инструкций DDL, что и другие объекты, хотя синтаксис немного отличается, чтобы определить возвращаемое значение:

CREATE FUNCTION имя_функции (входные_параметры)
RETURNS тип_данных
AS
BEGIN
текст_ функции
RETURN выражение
END

В списке входных параметров должны быть указаны типы данных и, в случае необходимости, значения по умолчанию, аналогично хранимым процедурам (параметр = умолчание). Параметры функции отличаются от параметров хранимых процедур тем, что даже если определены значения по умолчанию, параметры все равно должны присутствовать в вызове функции (т.е. параметры с определенными по умолчанию значениями все равно обязательны). Чтобы запросить значение по умолчанию при вызове функции, ей передается ключевое слово default.

Следующая скалярная функция выполняет простую арифметическую операцию; ее второй параметр имеет значение по умолчанию:

CREATE FUNCTION dbo.Multiply (@A int, @B int = 3)

Скалярные функции могут использоваться в любом месте выражений, где допустимо одно значение. Пользовательские скалярные функции должны всегда вызываться с помощью двухкомпонентного имени (владелец.имя). В следующем примере продемонстрирован вызов ранее созданной функции Multiply:

SELECT dbo.Multiply(7, DEFAULT)

Следующий код создает функцию, возвращающую имя заданного клиента в формате Фамилия И.

CREATE FUNCTION getFICust (@IdCust int)

DECLARE @result varchar(25)

SELECT @result = LName + ‘ ‘ + SUBSTRING(FName, 1, 1) + ‘.’

WHERE IdCust = @IdCust

Тестирование созданной функции:

SELECT dbo.getFICust(IdCust) AS CustName

ORDER BY LName, FName

Задание для самостоятельной работы: Создайте скалярные пользовательские функции, возвращающие:

· Количество товара на складе по заданному уникальному идентификатору товара;

· Суммарную стоимость товаров в заданном заказе.

Источник

Что значит скалярная функция

С SQL Server вы можете создавать ваши собственные функции, добавляющие и расширяющие функции, предоставляемые системой. Функции могут получать 0 или более параметров и возвращать скалярное значение или таблицу. Входные параметры могут быть любого типа, исключая timestamp, cursor, table.

Сервер SQL поддерживает три типа функций определенных пользователем:

1. Создание хранимой функции

Создание функций очень похоже на создание процедур и объектов просмотра. эедаром мы рассматриваем все эти темы в одной главе. Для создания функции используется оператор CREATE FUNCTION. В зависимости от типа, Объявление будет отличаться. э ассмотрим все три типа объявления.

Функция, возвращающая таблицу:

2. Скалярные функции в Transact-SQL

Давайте для примера создадим функцию, которая будет возвращать скалярное значение. эапример, результат перемножение цены на количество указанного товара. Товар будет идентифицироваться по названию и дате, ведь мы договорились, что сочетание этих полей дает уникальность. эо будьте осторожны, при тестировании запроса, если в разделе 3.2.8 вы выполнили запрос на изменение данных и создали дубликаты покупок за 1.1.2005-го года.

Итак, посмотрим сначала на код создание скалярной функции:

После оператора CREATE FUNCTION мы указываем имя функции. Далее, в скобках идут параметры, которые необходимо передать. Да, параметры должны передаваться через запятую в круглых скобках. В этом объявление отличается от процедур и эту разницу необходимо помнить.

Далее указывается ключевое слово RETURNS, за которым идет описание типа возвращаемого значения. Для скалярной функции это могут быть любые типы (строки, числа, даты и т.д.).

Код, который должна выполнять функция пишется между ключевыми словами BEGIN (начало) и END (конец). В коде можно использовать любые операторы Transact-SQL, которые мы изучали ранее. Итак, объявление нашей функции в упрощенном виде можно описать следующим образом:

Между ключевыми словами BEGIN и END у нас выполняется следующий код:

В первой строке объявляется переменная @Summ. Она нужна для хранения промежуточного результата расчетов. Далее выполняется запрос SELECT, в котором происходит поиск строки по дате и названию товара в таблице товаров. В найденной строке перемножаются поля цены и количества, и результат записывается в переменную @Summ.

Обратите внимание, что в конце запроса стоит знак точки с запятой. Каждый запрос должен заканчиваться этим символом, но в большинстве примеров мы этим пренебрегали, но в функции отсутствие символа «;» может привести к ошибке.

В последней строке возвращаем результат. Для этого нужно написать ключевое слово RETURN, после которого пишется возвращаемое значение или переменная. В данном случае, возвращаться будет содержимое переменной @Summ.

Так как функция скалярная, то и возвращаемое значение должно быть скалярным и при этом соответствовать типу, описанному после ключевого слова RETURNS.

3. Использование функций

Как выполнить такую функцию? Да также, как и многие другие системные функции (например, GETDATE()). эапример, следующий пример использует функцию в операторе SELECT:

В этом примере, оператор SELECT возвращает результат выполнения функции GetSumm. Функция принадлежит пользователю dbo, поэтому перед именем я указал владельца. После имени в скобках должны быть перечислены параметры в том же порядке, что и при объявлении функции. В данном примере я запрашиваю затраты на картофель, купленный 3.3.2005.

Выполните следующий запрос и убедитесь, что он вернул тот же результат, что и созданная нами функция:

Функции можно использовать не только в операторе SELECT, но и напрямую, присваивая значение переменной. эапример:

В этом примере мы объявили переменную @Summ типа numeric(10,2). Именно такой тип возвращает функция. В следующей строке переменной присваивается результат выполнения Summ, с помощью SET.

Давайте посмотрим, что произойдет, если передать функции такие параметры, при которых запрос функции вернет более одной строки. В нашей таблице товаров сочетание даты и название не дает уникальности, потому что мы ее нарушили. Первичного ключа в таблице также нет, и среди товаров у меня есть четыре строки, которые имеют свои точные копии. э­то нарушает правило уникальности строк в реляционных базах, но очень наглядно показывает, что в реальной жизни нарушать его нельзя.

Итак, в моей таблице есть две покупки хлеба 1.1.2005-го числа. Попробую запросить у функцию сумму:

э езультатом будет только одно число, хотя строки две. э какую строку из двух вернул сервер? эикто точно сказать не может, потому что они обе одинаковые и без единого различия. Поэтому сервер скорей всего вернул первую из строк.

4. Функция, возвращающая таблицу

В следующем примере мы создаем функцию, которая будет возвращать в качестве результата таблицу. В качестве примера, создадим функцию, которая будет возвращать таблицу товаров, и для каждой строки рассчитаем произведение колонок количества и цены:

эачало функции такое же, как у скалярной – указываем оператор CREATE FUNCTION и имя функции. Я специально создал эту функцию без параметров, чтобы вы увидели, как это делается. эе смотря на то, что параметров нет, после имени должны идти круглые скобки, в которых не надо ничего писать. Если не указать скобок, то сервер вернет ошибку и функция не будет создана.

э азница есть и в секции RETURNS, после которой указывается тип TABLE, что говорит о необходимости вернуть таблицу. После этого идет ключевое слово AS и RETURN, после которого должно идти возвращаемое значение. Для функции данного типа в секции RETURN нужно в скобках указать запрос, результат которого и будет возвращаться функцией.

Когда пишете запрос, то все его поля должны содержать имена. Если одно из полей не имеет имени, то результатом выполнения оператора CREATE FUNCTION будет ошибка. В нашем примере последнее поле является результатом перемножения полей «Цена» и «Количество», а такие поля не имеют имени, поэтому мы его задаем с помощью ключевого слова AS.

Посмотрим, как можно использовать такую функцию с помощью оператора SELECT:

Так как мы используем простой оператор SELECT, то мы можем и ограничивать вывод определенными строками, с помощью ограничений в секции WHERE. эапример, в следующем примере выбираем из результата функции только те строки, в которых поле «Количество» содержит значение 1:

Функция возвращает в качестве результата таблице, которую вы можете использовать как любую другую таблицу базы данных. Давайте создадим пример в котором можно будет увидеть использование функции в связи с таблицами. Для начала создадим функцию, которая будет возвращать идентификатор работников таблицы tbPeoples и объединенные в одно поле ФИО:

Функция возвращает нам идентификатор строки, с помощью которого мы легко можем связать результат с таблицей телефонов. Попробуем сделать это с помощью простого SQL запроса:

Как видите, функции, возвращающие таблицы очень удобны. Они больше, чем процедуры похожи на объекты просмотра, но при этом позволяют принимать параметры. Таким образом, можно сделать так, чтобы сама функция возвращала нам только то, что нужно. Вьюшки такого не могут делать по определению. Чтобы получить нужные данные, вьюшка должна выполнить свой SELECT запрос, а потом уже во внешнем запросе мы пишем еще один оператор SELECT, с помощью которого ограничивается вывод до необходимого. Таким образом, выполняется два запроса SELECT, что для большой таблицы достаточно накладно. Функция же может сразу вернуть только то, что нужно.

э ассмотрим пример, функция GetPeoples у нас возвращает все строки таблицы. Чтобы получить только нужную фамилию, нужно писать запрос типа:

В этом случае будут выполняться два запроса: этот и еще один внутри функции. эо если передавать фамилию в качестве параметра в функцию и там сделать секцию WHERE, то можно обойтись и одним запросом SELECT:

5. Многооператорная функция возвращающая таблицу

Все функции, созданные в разделе 3.3.5 могут возвращать таблицу, сгенерированную только одним оператором SQL. э как же тогда сделать возможность выполнять несколько операций? эапример, вы можете захотеть выполнять дополнительные проверки входных параметров для обеспечения безопасности. Проверки лишними не бывает, особенно входных данных и особенно, если эти входные данные указываются пользователем.

Следующий пример показывает, как создать функцию, которая может вернуть в качестве результата таблицу, и при этом, в теле функции могут выполняться несколько операторов:

э­то упрощенный вид создания процедуры. Более полный вид мы рассматривали в начале главы, а сейчас я упростил объявление, чтобы проще было его разбирать.

Объявление больше похоже на создание скалярных функций. Первая строка без изменений. В секции RETURNS объявляется переменная, которая имеет тип TABLE. После этого, в скобках нужно описать поля результирующей таблицы. После ключевого слова AS идtт пара операторов BEGIN и END, между которыми может выполняться какое угодно количество операций. Выполнение операций заканчивается ключевым словом RETURN.

Вот тут есть одно отличие от скалярных функций – после RETURN мы указывали имя переменной, значение которой должно стать результатом. В данном случае ничего указывать не надо. Мы уже объявили переменную в секции RETURNS и описали формат этой переменной. В теле функции мы можем и должны наполнить эту переменную значениями и именно это попадет в результат.

Теперь посмотрим на пример создания функции:

В данном примере в качестве результата объявлена переменная @ret, которая является таблицей из двух полей «idPeoples» типа int и «vcFIO» типа varchar длинной в 50 символов. В теле функции в эту таблицу записываются значения из таблицы tbPeoples и выполняется оператор RETURN, завершающий выполнение функции.

В использовании, такая функция ничем не отличается от рассмотренных ранее. эапример, следующий запрос выбирает все данные, которые возвращает функция:

6. Опции функций

При создании функций могут использоваться следующие опции SCHEMABINDING (привязать к схеме) и/или ENCRYPTION (шифровать текст функции). Если вторая опция нам уже известна по вьюшкам и процедурам (позволяет шифровать исходный код функции в системных таблицах), то вторая встречается впервые, но при этом предоставляет удобное средство защиты данных.

Если функция создана с опцией SCHEMABINDING, то объекты базы данных, на которые ссылается функция, не могут быть изменены (с использованием оператора ALTER) или удалены (с помощью оператора DROP). эапример, следующая функция использует таблицу tbPeoples и при этом используется опция SCHEMABINDING:

Функция может быть связанной со схемой, только если следующие ограничения истины:

Создайте функцию и попробуйте после этого удалить таблицу tbPeoples.

В ответ на это сервер выдаст сообщение с ошибкой о том, что объект не может быть удален, из-за присутствия внешнего ключа. Даже если избавиться от ключа, удаление будет невозможно, потому что на таблицу ссылается функция, привязанная к схеме.

Чтобы увидеть сообщение без удаления ключа, давайте добавим к таблице колонку, а потом попробуем ее удалить:

Создание пройдет успешно, а вот во время удаления произойдет ошибка, с сообщением о том, что существует ограничение, которое зависит от колонки. Мы же не создавали никаких ограничений, а просто добавили колонку и попытались ее удалить. Ограничение уже давно существует, но не на отдельную колонку, а на все колонки таблицы и это ограничение создано функцией GetPeoples2, которая связана со схемой.

7. Изменение функций

Вы можете изменять функцию с помощью оператора ALTER FUNCTION. Общий вид для каждого варианта функции отличается. Давайте рассмотрим каждый из них.

1. Общий вид команды изменения скалярной функции:

2. Общий вид изменения функции, возвращающей таблицу:

3. Общий вид команды изменения функции с множеством операторов, возвращающей таблицу.

Следующий пример показывает упрощенный вариант команды, изменяющей функцию:

8. Удаление функций

Если вы внимательно читали об объектах просмотра и функциях, то не трудно догадаться, как можно удалить функцию. Конечно же для этого используется оператор DROP FUNCTION:

Источник

Скалярная функция

В самом общем случае, числовая функция — это функция, принимающая значения в области вещественных чисел и которая задана на произвольном (чаще всего) метрическом пространстве. Такова, например, индикаторная или характеристическая функция множества. Другой пример числовой функции — это функция расстояния (или, что то же самое, метрика).

Числовые функции, заданные на множестве вещественных или комплексных чисел называются функциями соответственно вещественного или комплексного переменного и являются предметом рассмотрения в анализе:

Важнейший предмет рассмотрения в анализе — представление числовых функций в виде системы приближений (числовых и функциональных рядов).

Числовые функции обладают как общими свойствами, которыми могут обладать отображения произвольных метрических пространств (например, непрерывность), так и рядом свойств, непосредственно связанных с природой числовых пространств. Таковы свойства

Числовые функции широко используются на практике при решении прикладных задач.

Содержание

Свойства

Свойства, связанные с отношением порядка

(Строго) возрастающая или убывающая функция называется (строго) монотонной.

Периодичность

Чётность

Экстремумы функции

График функции

Примеры

Способы задания функции

ТабличныйС помощью таблицы значений

x	0	1	2	3	4	5	6	7	8	9
y	1	1	2	3	5	8	13	21	34	55

Аналитический способ

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде. Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно. Функция может быть определена разными формулами на разных участках области своего задания. Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.

Табличный способ

Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:

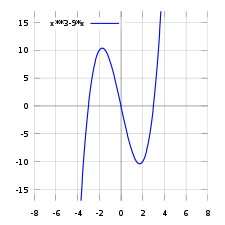
Графический способ

Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.

Рекурсивный способ

Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.

Словесный способ

Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.

Классы числовых функций

Исторический очерк

Появление понятия

Математический термин «функция» впервые появился в 1673 году у Лейбница, и притом не совсем в современном его понимании: Лейбниц вначале называл функцией различные отрезки, связанные с какой-либо кривой (например, абсциссы её точек). Позже, однако, в переписке с Иоганном Бернулли (1694) содержание термина расширяется и в конце концов становится синонимом «аналитически заданной зависимости».

В первом печатном курсе «Анализа бесконечно малых для познания кривых линий» Лопиталя (1696) термин «функция» не употребляется.

Первые попытки определения

В начале XVIII века были получены разложения всех стандартных функций и многих других. Благодаря, в основном, Эйлеру (1748) были уточнены их определения. Эйлер впервые ясно определил показательную функцию, а также логарифмическую как обратную к ней, и дал их разложения в ряд. До Эйлера многие математики считали, например, тангенс тупого угла положительным; Эйлер дал современные определения всех тригонометрических функций (сам термин «тригонометрическая функция» предложил Клюгель в 1770 году).

В приложениях анализа появляется множество новых трансцендентных функций. Когда Гольдбах и Бернулли попытались найти непрерывный аналог факториала, молодой Эйлер сообщил в письме Гольдбаху о свойствах гамма-функции (1729, название принадлежит Лежандру). Через год Эйлер открыл бета-функцию, и далее неоднократно возвращался к этой теме. Гамма-функция и связанные с ней (бета, дзета, цилиндрические (Бесселя)) находят многочисленные применения в анализе, а также в теории чисел, а дзета-функция Римана оказалась незаменимым инструментом для изучения распределения простых чисел в натуральном ряду.

В 1757 году Винченцо Риккати, исследуя секторы гиперболы, вводит гиперболические функции ch, sh (именно с такими обозначениями) и перечисляет их основные свойства. Немало новых функций возникло в связи с неинтегрируемостью различных выражений. Эйлер определил (1768) интегральный логарифм (название предложил И. Зольднер, 1809), Л. Маскерони — интегральные синус и косинус (1790). Вскоре появляется и новый раздел математики: специальные функции.

С этим пёстрым собранием надо было что-то делать, и математики приняли радикальное решение: все функции, независимо от их происхождения, были объявлены равноправными. Единственное требование, предъявляемое к функции — определённость, причём имеется в виду не однозначность самой функции (она может быть и многозначной), а недвусмысленность способа вычисления её значений.

Первое общее определение функции встречается у Иоганна Бернулли (1718): «Функция — это величина, составленная из переменной и постоянной». В основе этого не вполне отчётливого определения лежит идея задания функции аналитической формулой. Та же идея выступает и в определении Эйлера, данном им во «Введении в анализ бесконечных» (1748): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств».

Всё же в XVIII веке отсутствовало достаточно ясное понимание различия между функцией и её аналитическим выражением. Это нашло отражение в той критике, которой Эйлер подверг решение задачи о колебании струны, предложенное Бернулли (1753). В основе решения Бернулли лежало утверждение о возможности разложить любую функцию в тригонометрический ряд. Возражая против этого, Эйлер указал на то, что подобная разложимость доставляла бы для любой функции аналитическое выражение, в то время как функция может и не иметь его (она может быть задана графиком, «начертанным свободным движением руки»).

Под влиянием теории бесконечных рядов, которые давали алгебраическое представление почти любой гладкой зависимости, наличие явной формулы постепенно перестало быть обязательным для функции. Логарифм или показательная функция, например, вычисляются как пределы бесконечных рядов; такой подход распространился и на другие нестандартные функции. С рядами стали обращаться как с конечными выражениями, первоначально никак не обосновывая корректность операций и даже не гарантируя сходимость ряда.

Начиная с «Дифференциального исчисления» (1755), Эйлер фактически принимает современное определение числовой функции как произвольного соответствия чисел [4] :

Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых.

Общее определение

Близко к современному и определение Лобачевского:

Таким образом, современное определение функции, свободное от упоминаний об аналитическом задании, обычно приписываемое Дирихле, неоднократно предлагалось и до него. Вот определение Дирихле (1837):

К концу XIX века понятие функции перерастает рамки числовых систем. Первыми это сделали векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.

Примеры

Неявные функции

Функции могут быть заданы при помощи других функций и уравнений.

Источник