Что значит середины отрезков совпадают

Сравнение отрезков

Одной из простейших геометрических фигур является отрезок. Для того чтобы сравнивать отрезки, можно использовать два способа:

Метод наложения:

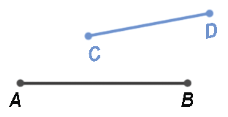
Пусть нам даны два отрезка AB и СD:

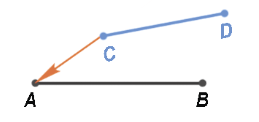
Совместим начало отрезка AB и СD (точки A и С).

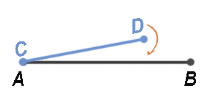
Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.

Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.

Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.

Рассмотрим еще одну пару отрезков HG и ST.

Совместим начало отрезка HG и ST.

Затем повернем отрезок ST так, чтобы он совпал с отрезком HG.

В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.

Вывод:

Измерение длин:

Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.

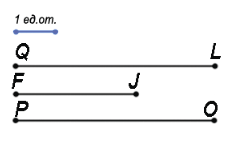
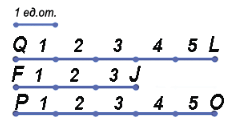
Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.

Наложим единичный отрезок на данные.

Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.

Поделись с друзьями в социальных сетях:

Источник

Отрезок

Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.

Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.

Длина отрезка

Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:

Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:

длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.

Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:

Свойства длин отрезков:

Равные отрезки

Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.

Пример. Возьмём два отрезка CD и LM:

Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:

Значит длины отрезков равны, следовательно CD = LM.

Сравнение отрезков

Сравнить два отрезка — это значит определить, равны они, или один больше другого.

Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.

Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.

При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.

Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):

Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):

CA > CB или CB Пример. Сравнить длину отрезков AB и AC.

Так как отрезок AB имеет большую длину, чем отрезок AC, то

Так как отрезки AB и AC имеют одинаковую длину, то

Если при измерении отрезков их длины равны, то и отрезки равны.

Середина отрезка

Середина отрезка — это точка, делящая отрезок на две равные части.

Источник

Отрезок. Ломаная линия

Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.

Рис. 1 Отрезок на прямой

Рис. 2 Несколько отрезков на прямой

Отрезок делит прямую линию на три объекта (смотри рисунок 3):

То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.

Рис. 3 Отрезок и лучи прямой

Рис. 4 Отрезок без прямой

Рис. 5 Отрезок и принадлежащие ему точки

Так, на рисунке 5 видно, что:

В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.

Рис. 6 Отрезок и части отрезка

Построение и измерение отрезка

Произвольный отрезок можно построить двумя способами:

Рис. 7 Построение произвольного отрезка

Измерить отрезок можно:

Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).

Рис. 8 Сравнение отрезков

На рисунке 8 видно, что:

Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.

Длина отрезка – это расстояние между концами этого отрезка.

Равные отрезки — это такие отрезки, которые имеют одинаковую длину.

На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?

Рис. 9 Измерение длины отрезка

Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.

Рис. 10 Построение отрезка заданной длины

Отрезок — это самое короткое расстояние между двумя точками.

В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.

Рис. 11 Кривая, ломаная, отрезок

Ломаная линия

Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.

Рис. 12 Ломаная линия

На рисунке 12 видно, что:

Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.

Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.

Рис. 12. Замкнутая и разомкнутая ломаные линии

Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.

Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.

Рис. 13. Самопересекающиеся ломаные линии

Источник

Координаты середины отрезка

Что такое середина отрезка

Отрезок — это геометрическая фигура, представляющая собой ограниченный с двух сторон участок прямой.

Пусть точки A и B не совпадают. Если провести через них прямую, то образуется отрезок AB или BA, который ограничен точками A и B. Данные точки являются концами отрезка.

Длина отрезка — это расстояние между двумя точками, ограничивающими данный отрезок. Длина отрезка AB обозначается как модуль данной геометрической фигуры, то есть |AB|.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Серединой отрезка является такая точка C, принадлежащая отрезку AB, которая расположена в центре данного отрезка, то есть |AC|=|CB|.

Правила нахождения координат середины отрезка, формулы

Середина отрезка на координатной прямой

Предположим, что несовпадающие точки A и B лежат на координатной прямая Ох. Известно, что A и B соответствуют действительные числа x_A и x_B, а точка С делит AB пополам. Определите координату x_C, соответствующую С.

Так как C — это середина AB, то справедливо следующее равенство:

Вычислим расстояние между A и C, а также между C и B. Для этого определим модуль разницы их координат. На математическом языке это будет иметь вид:

Опустим знак модуля и получим справедливость двух выражений:

Исходя из первого равенства, получим формулу нахождения x_C, согласно которой координата точки С равна половине суммы координат A и B:

Следствием второго равенства будет следующее утверждение:

Это противоречит заданным условиям, следовательно, формула определения координат середины отрезка выглядит так:

Середина отрезка на плоскости

В декартовой системе координат Oxy расположены две точки A(x_A,y_A) и B(x_B,y_B), которые не совпадают между собой. Точка C является центром AB. Необходимо произвести вычисление координат x_C и y_C, соответствующих С.

Пусть произвольные точки А и В лежат на одной координатной прямой, а также не принадлежат прямым, располагающимся перпендикулярно к оси абсцисс или ординат. Опустим от заданных точек A, B, C перпендикуляры на ось x на ось y. Полученные точки пересечения с осями координат A_x, A_y; B_x, B_y; C_x, C_y — это проекции исходных точек.

По построению прямые AA_x, BB_x, CC_x относительно друг друга находятся параллельно. Прямые AA_y, BB_y, CC_y не пересекаются, то есть являются параллельными. Согласно равенству AB=BC, далее применим теорему Фалеса и получим:

Это значит, что C_x и C_y являются серединами отрезков A_xB_x и A_yB_y соответственно. Теперь воспользуемся формулой определения координат середины отрезка на координатной прямой и получим:

Данные формулы подходят для вычисления координат середины отрезка в случае его расположения на осях абсцисс и ординат, а также при перпендикулярности одной из них. Следовательно, координаты центра отрезка AB, находящегося в плоскости и ограниченного точками A(x_A,y_A) и B(x_B,y_B), вычисляются следующим образом:

Середина отрезка в пространстве

Допустим, что в трехмерной системе координат Oxyz любые две точки с соответствующими им координатами A(x_A, y_A, z_A) и B(x_B, y_B, z_B). C(x_C, y_C, z_C) — это центр АВ. Задание заключается в том, чтобы определить x_C, y_C, z_C.

Проведем от исходных точек перпендикуляры к прямым Ox, Oy и Oz. Образовавшиеся точки пересечения с координатными осями — A_x, A_y, A_z; B_x, B_y, B_z; C_x, C_y, C_z — проекции точек A, B, C на них.

Воспользуемся теоремой Фалеса:

Исходя из полученных равенств следует, что C_x, C_y, C_z — делят A_xB_x, A_yB_y, A_zB_z пополам, то есть являются серединами перечисленных отрезков. Значит, для определения координат центра AB с концами A(x_A,y_A,z_A) и B(x_B,y_B,z_B) используем формулу:

Метод с использованием координат радиус-векторов концов отрезка

Трактовка векторов в алгебре позволяет составить формулу для расчета координат середины отрезка.

Дано: прямоугольная система координат Oxy, в которой лежат произвольные точки A(x_A,y_A) и B(x_B,y_B), а также C, делящая пополам отрезок, ограниченный A и B.

По определению действий над вектором в геометрии:

Это значит, что С — это центр диагоналей.

Произведем подстановку в формулу (1):

Получили формулу определения координат середины отрезка, находящегося в декартовой системе координат:

По аналогично схеме можно вывести формулу для расчета координат центра отрезка, лежащего в пространстве:

Примеры решения задач

Дано: в декартовой системе координат имеются точки M(5,4) и N(1,−2). Найти координаты середины отрезка MN.

Пусть точка O — центр MN. Тогда вычислим ее координаты, подставив в формулы:

Точка O имеет координаты (3,1).

Дано: треугольник ABC лежит в прямоугольной системе координат. Известны координаты его вершин: A(7,3), B(−3,1), C(2,4). Вычислите длину медианы АМ.

Поскольку АМ является медианой треугольника ABC, то точка М делит сторону ВС на два равных отрезка, то есть является серединой отрезка ВС. Отсюда можно вычислить координат точки М:

Теперь, зная координаты начала и конца отрезка АМ, применим формулу нахождения расстояния между точками:

Источник

Что должно быть одинаковым в двух отрезках, чтобы они соответствовали друг другу?

Сегменты линий совпадают если у них одинаковая длина. … Для линейных сегментов выражение «конгруэнтно» похоже на выражение «равно». Вы могли бы сказать «длина линии AB равна длине линии PQ». Но в геометрии правильный способ сказать, что это «отрезки AB и PQ конгруэнтны» или «AB конгруэнтны PQ».

Кроме того, есть ли у сегмента уникальная средняя точка?

Теорема 9.2: Середина сегмент уникален. … Вам понадобится отрезок линии; назовите это AB. Вам также понадобятся две средние точки, которые вы можете назвать M и N.

При этом как узнать, совпадают ли сегменты?

Конгруэнтные сегменты просто отрезки равной длины. Конгруэнтный означает равный. Сегменты конгруэнтных линий обычно обозначаются путем рисования одинакового количества маленьких линий в середине сегментов, перпендикулярных сегментам. … Важная часть состоит в том, что они равны или совпадают.

Также знать, как вы доказываете, что линии совпадают? Если две параллельные прямые пересекаются поперечной, то соответствующие углы конгруэнтны. Если две прямые пересекаются трансверсалью и соответствующие углы совпадают, то прямые параллельны.

Что это значит, если два угла совпадают?

У биссектрисы одинаковая середина?

Конгруэнтны ли обе стороны средней точки?

Теорема: отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и совпадает с половиной третьей стороны. Доказательство. Рассмотрим треугольник ABC, середина которого обозначена M.…

Могут ли быть похожими два отрезка?

Следовательно, утверждение, что «два отрезка линии совпадают, если они имеют одинаковую длину» правда. Примечание. Любые отрезки линии совпадают, если они имеют одинаковую длину. Однако они не обязательно должны быть параллельны. Они могут быть под любым углом или ориентированы на плоскости.

Что доказывает, что две линии параллельны?

Если две прямые пересекаются трансверсалью, так что соответствующие углы совпадают, то прямые параллельны. Если две линии пересекаются трансверсалью, так что альтернативные внутренние углы совпадают, тогда линии параллельны.

Какие пять способов доказать, что две прямые параллельны?

Способы доказательства параллельности двух линий

Могут ли 2 линии совпадать?

Два отрезка совпадают, если они имеют одинаковую длину.. У них не обязательно должно быть одинаковое положение или ориентация. … Однако соответствие отрезков прямой отличается от равенства отрезков в том смысле, что равенство сравнивает расстояние. Например, AB = CD, потому что AB и CD представляют длину линий.

Как доказать, что две линии параллельны?

Если две линии пересекаются трансверсалью и чередующиеся внешние углы равны, то две прямые параллельны. Углы могут быть равными или равными; вы можете заменить слово «равный» в обеих теоремах на «конгруэнтный», не затрагивая теорему. Итак, если ∠B и ∠L равны (или совпадают), прямые параллельны.

Какие два угла должны совпадать?

Все углы, которые внешние углы, внутренние углы, альтернативные углы или соответствующие углы все конгруэнтны.

Что такое SSS SAS ASA AAS?

SSS означает «сторона, сторона, сторона”И означает, что у нас есть два треугольника, все три стороны которых равны. Если три стороны одного треугольника равны трем сторонам другого треугольника, треугольники конгруэнтны. SAS (сторона, угол, сторона)

Что происходит, когда два отрезка линии имеют одинаковую середину?

Средние точки сегмента

Как это называется, когда два сегмента имеют одинаковую середину?

Как найти середину имени?

Середина отрезка линии

Где середина треугольника?

Как объяснить мидпойнт?

Какова теорема о мидпойнте?

Теорема о средней точке утверждает, что ” Отрезок в треугольнике, соединяющий середину двух сторон треугольника, считается параллельным его третьей стороне и также составляет половину длины третьей стороны.

Что произойдет, если два сегмента совпадают?

Линии не лежат в одной плоскости?

Что происходит, когда две параллельные линии пересекаются трансверсалью?

Если две параллельные прямые пересекаются трансверсалью, то соответствующие углы совпадают. Две прямые, пересеченные трансверсалью, параллельны, ЕСЛИ И ТОЛЬКО ЕСЛИ соответствующие углы совпадают. … Если внутренние углы на одной стороне поперечной в сумме равны 180, то прямые параллельны.

При пересечении двух параллельных прямых образуются поперечные углы?

Как узнать, параллельны ли две линии углам?

Во-первых, если соответствующие углы, углы, которые находятся на одном и том же углу на каждом пересечении, равны, тогда прямые параллельны. Во-вторых, если чередующиеся внутренние углы, углы, которые находятся на противоположных сторонах поперечной и внутри параллельных линий, равны, то линии параллельны.

Источник