Что значит сдвинуть число на один двоичный разряд вправо
Русские Блоги
Операция двоичного сдвига, битовая операция
1. Фон
Каждый из наших языков в конечном итоге будет выполняться компилятором, преобразованным в машинный язык, поэтому прямое использование основного языка не требует преобразования компилятора для получения более высокой эффективности выполнения, конечно, читаемость может быть снижена, это также Почему сборка в большинстве случаев быстрее. Разумное использование битовых операций в проекте может повысить эффективность выполнения нашего кода.
В системе iOS битовые операции чаще всего встречаются в перечислениях и редко встречаются где-либо еще, потому что битовые операции являются основным компьютерным языком, а в разработке iOS и Objective-C, и Swift принадлежат к языкам программирования высокого уровня с большим количеством битовых операций. Все они инкапсулированы Apple.Мы заботимся только о вызываемом интерфейсе и не заботимся о внутренней реализации.
10: Принципы компьютерных вычислений
#### Сложение и умножение
Приведите простой пример, чтобы увидеть, как ЦП выполняет вычисления, например эту строку кода.
Вычислите сумму двух чисел, потому что компьютер работает в двоичном формате, поэтому переменная int, которую мы указали выше, будет преобразована в двоичную форму в машине и добавлена
Давайте снова посмотрим на умножение и выполним следующий код
С помощью приведенного выше расчета мы видим, что когда a умножается на b и если b удовлетворяет 2 ^ N, это эквивалентно сдвигу двоичных данных a влево на N бит и помещению их в код. Мы можем записать это такa 0110 Как упоминалось выше, битовые операции, часто встречающиеся в iOS, находятся в перечислениях, поэтому преобразование цвета должно быть второй наиболее распространенной сценой битовых операций, помимо перечислений. Например, когда дизайнеры предоставляют нам черновик, они обычно отмечают на нем значения цвета в шестнадцатеричном формате. Но UIColor в iOS не поддерживает использование шестнадцатеричных данных для инициализации. Итак, нам нужно преобразовать шестнадцатеричное значение цвета в UIColor. UIColor обычно инициализируется значением входящего RGB, а диапазон значений каждого цвета составляет 0 255 в десятичном виде, и студенты-дизайнеры также предоставляют шестнадцатеричные данные, поэтому это необходимо изменить в операционной системе. Данные двух баз объединяются в двоичный код для вычислений, в котором используются битовые операции. Вот пример шестнадцатеричного значения цвета, например0xffa131Мы должны сначала понять его состав, если хотим преобразовать 0x или 0X: шестнадцатеричный идентификатор, указывающий, что за ним следует шестнадцатеричное значение, не имеющее значения для самого значения. Значение R в цвете ff, преобразованное в двоичное, составляет 1111 1111 Значение G в цвете a1, преобразованное в двоичное, как 1010 0001. 31 Значение B цвета, преобразованное в двоичное, как 0011 0001 Вышеуказанное значение цвета преобразуется в двоичное как1111 1111 1010 0001 0011 0001 (каждый шестнадцатеричный бит соответствует 4 двоичным битам, если количество бит недостаточно, не забудьте заполнить старший бит нулем) Вообще говоря, шестнадцатеричные цвета расположены в указанном выше порядке RGB, но это не фиксировано. Иногда к нему может быть добавлено значение A (Alpha). Конкретная ситуация зависит от дизайна. В этой статье в качестве примеров используются общие случаи. Таким образом, нам нужно только преобразовать значение соответствующего бита в десятичное, а затем /255.0f, чтобы получить значение цвета RGB, которое можно преобразовать в UIColor. #### Код конверсии Сначала укажите код, затем проанализируйте Можно увидеть общий принцип синтаксического анализа каждого значения RGB и преобразования его в UIColor. Сначала сделайте первый шаг, чтобы преобразовать значение красного. Давайте проследим порядок действий шаг за шагом (по умолчанию параметры подставляются, а вместо hexColor используется 0xffa131) 0xffa131 & 0xFF0000 Сдвиньте результат, полученный на предыдущем шаге, на 16 бит вправо, чтобы получить0000 0000 0000 0000 1111 1111Старшие нули можно игнорировать, это тоже конечный результат / 255.0f На этом этапе вы должны знать, что диапазон значений, переданный в UIColor, составляет 0 1, поэтому нам нужно преобразовать Последующее значение G и значение B одинаковы, но все обращают внимание на количество бит.Стоит отметить, что битовая операция над двумя двоичными числами должна обеспечивать совпадение цифр этих двух чисел.Старшая цифра числа с недостаточным количеством цифр должна быть заполнена 0. Мы также говорили об использовании битовых операций при перечислении, давайте сами напишем перечисление (псевдокод) В iOS мы можем использовать XOR для шифрования и дешифрования. Характеристики XOR следующие. Выше мы можем рассматривать A как данные, которые необходимо зашифровать, B как ключ и C как зашифрованные данные. Например: Принцип очень прост, потому что двоичная система состоит из двух в один, когда оно превысит 1, оно изменится на 0 и войдет в один бит. В это время операция ** & ** с 00001 определенно будет 0, в противном случае это не ноль. Эта эффективность записи будет выше. В C# имеется возможность сдвигать двоичные разряды, составляющие целое значение, влево или вправо на заданную величину. Для этой цели в C# определены два приведенных ниже оператора сдвига двоичных разрядов. Ниже приведена общая форма для этих операторов: При сдвиге влево все двоичные разряды в указываемом значении сдвигаются на одну позицию влево, а младший разряд сбрасывается в нуль. При сдвиге вправо все двоичные разряды в указываемом значении сдвигаются на одну позицию вправо. Если вправо сдвигается целое значение без знака, то старший разряд сбрасывается в нуль. А если вправо сдвигается целое значение со знаком, то разряд знака сохраняется. Напомним, что для представления отрицательных чисел старший разряд целого числа устанавливается в 1. Так, если сдвигаемое значение является отрицательным, то при каждом сдвиге вправо старший разряд числа устанавливается в 1. А если сдвигаемое значение является положительным, то при каждом сдвиге вправо старший разряд числа сбрасывается в нуль. При сдвиге влево и вправо крайние двоичные разряды теряются. Восстановить потерянные при сдвиге двоичные разряды нельзя, поскольку сдвиг в данном случае не является циклическим. Ниже приведен пример программы, наглядно демонстрирующий действие сдвига влево и вправо. В данном примере сначала задается первоначальное целое значение, равное 1. Это означает, что младший разряд этого значения установлен. Затем это целое значение сдвигается восемь раз подряд влево. После каждого сдвига выводятся восемь младших двоичных разрядов данного значения. Далее процесс повторяется, но на этот раз 1 устанавливается на позиции восьмого разряда, а по существу, задается целое значение 128, которое затем сдвигается восемь раз подряд вправо. Результат выполнения этой программы выглядит следующим образом. Двоичные разряды соответствуют форме представления чисел в степени 2, и поэтому операторы сдвига могут быть использованы для умножения или деления целых значений на 2. Так, при сдвиге вправо целое значение удваивается, а при сдвиге влево — уменьшается наполовину. Разумеется, все это справедливо лишь в том случае, если крайние разряды не теряются при сдвиге в ту или иную сторону. Ниже приведен соответствующий пример. Ниже приведен результат выполнения этой программы. Особый класс операций представляют поразрядные операции. Они выполняются над отдельными разрядами числа. Они выполняются только над целыми числами (то есть над значениями типов byte, sbyte, int16, uint16, int, uint, int64, uint64, nativeint и unativeint.). Рассмотрим все поразрядные операции языка F#: Умножение производится поразрядно, и если у обоих операндов значения соответствующих разрядов равно 1, то операция возвращает 1, иначе возвращается число 0. Например: Во втором случае у нас вместо двойки число 4, у которого в первом разряде 1, так же как и у числа 5, поэтому в итоге получим (1*1, 0*0, 0 *1) = 100, то есть число 4 в десятичном формате. Похоже на логическое умножение, операция также производится по двоичным разрядам, но теперь возвращается единица, если хотя бы у одного числа в данном разряде имеется единица. Например: (логическое отрицание или инверсия) Еще одна поразрядная операция, которая инвертирует все разряды: если значение разряда равно 1, то оно становится равным нулю, и наоборот. Для записи чисел со знаком в F# применяется дополнительный код (two’s complement), при котором старший разряд является знаковым. Если его значение равно 0, то число положительное, и его двоичное представление не отличается от представления беззнакового числа. Например, 0000 0001 в десятичной системе 1. Чтобы получить из положительного числа отрицательное, его нужно инвертировать и прибавить единицу: Операции сдвига также производятся над разрядами чисел. Сдвиг может происходить вправо и влево. Здесь операция сдвигает число 4 (которое в двоичном представлении 100) на два разряда влево, то есть в итоге получается 10000 или число 16 в десятичном представлении. Здесь операция сдвигает число 16 (которое в двоичном представлении 10000) на один разряд вправо, то есть в итоге получается 1000 или число 8 в десятичном представлении. Таким образом, если исходное число, которое надо сдвинуть в ту или другую строну, делится на два, то фактически получается умножение или деление на два. Поэтому подобную операцию можно использовать вместо непосредственного умножения или деления на два. В этой статье я расскажу вам о том, как работают битовые операции. С первого взгляда они могут показаться вам чем-то сложным и бесполезным, но на самом деле это совсем не так. В этом я и попытаюсь вас убедить. Побитовые операторы проводят операции непосредственно на битах числа, поэтому числа в примерах будут в двоичной системе счисления. Я расскажу о следующих побитовых операторах: Битовые операции изучаются в дискретной математике, а также лежат в основе цифровой техники, так как на них основана логика работы логических вентилей — базовых элементов цифровых схем. В дискретной математике, как и в цифровой технике, для описания их работы используются таблицы истинности. Таблицы истинности, как мне кажется, значительно облегчают понимание битовых операций, поэтому я приведу их в этой статье. Их, тем не менее, почти не используют в объяснениях побитовых операторов высокоуровневых языков программирования. О битовых операторах вам также необходимо знать: Побитовое ИЛИ действует эквивалентно логическому ИЛИ, но примененному к каждой паре битов двоичного числа. Двоичный разряд результата равен 0 только тогда, когда оба соответствующих бита в равны 0. Во всех других случаях двоичный результат равен 1. То есть, если у нас есть следующая таблица истинности: 38 | 53 будет таким: Побитовое И — это что-то вроде операции, противоположной побитовому ИЛИ. Двоичный разряд результата равен 1 только тогда, когда оба соответствующих бита операндов равны 1. Другими словами, можно сказать, двоичные разряды получившегося числа — это результат умножения соответствующих битов операнда: 1х1 = 1, 1х0 = 0. Побитовому И соответствует следующая таблица истинности: Пример работы побитового И на выражении 38 & 53: Разница между исключающим ИЛИ и побитовым ИЛИ в том, что для получения 1 только один бит в паре может быть 1: Например, выражение 138^43 будет равно… С помощью ^ можно поменять значения двух переменных (имеющих одинаковый тип данных) без использования временной переменной. Также с помощью исключающего ИЛИ можно зашифровать текст. Для этого нужно лишь итерировать через все символы, и ^ их с символом-ключом. Для более сложного шифра можно использовать строку символов: Исключающее ИЛИ не самый надежный способ шифровки, но его можно сделать частью шифровального алгоритма. Побитовое отрицание инвертирует все биты операнда. То есть, то что было 1 станет 0, и наоборот. Вот, например, операция Результатом будет 20310 При использовании побитового отрицания знак результата всегда будет противоположен знаку исходного числа (при работе со знаковыми числами). Почему так происходит, узнаете прямо сейчас. Здесь мне стоит рассказать вам немного о способе представления отрицательных целых чисел в ЭВМ, а именно о дополнительном коде (two’s complement). Не вдаваясь в подробности, он нужен для облегчения арифметики двоичных чисел. Главное, что вам нужно знать о числах, записанных в дополнительном коде — это то, что старший разряд является знаковым. Если он равен 0, то число положительное и совпадает с представлением этого числа в прямом коде, а если 1 — то оно отрицательное. То есть, 10111101 — отрицательное число, а 01000011 — положительное. Чтобы преобразовать отрицательное число в дополнительный код, нужно инвертировать все биты числа (то есть, по сути, использовать побитовое отрицание) и добавить к результату 1. Например, если мы имеем 109: A+1 Побитовые сдвиги немного отличаются от рассмотренных ранее битовых операций. Побитовый сдвиг влево сдвигает биты своего операнда на N количество битов влево, начиная с младшего бита. Пустые места после сдвига заполняются нулями. Происходит это так: Как вы могли догадаться, >> сдвигает биты операнда на обозначенное количество битов вправо. Если операнд положительный, то пустые места заполняются нулями. Если же изначально мы работаем с отрицательным числом, то все пустые места слева заполняются единицами. Это делается для сохранения знака в соответствии с дополнительным кодом, объясненным ранее. Итак, теперь вы знаете больше о битовых операциях и не боитесь их. Могу предположить, что вы не будете использовать >>1 при каждом делении на 2. Тем не менее, битовые операции неплохо иметь в своем арсенале, и теперь вы сможете воспользоваться ими в случае надобности или же ответить на каверзный вопрос на собеседовании. Битовые операции в Java. Java позволяет манипулировать числами на битовом уровне, что означает работу с битами, из которых состоит число, а именно с его представлением в двоичной системе счисления. Что же такое система счисления вообще и двоичная система в частности? Двоичная арифметика. Таблица сложения Таблица вычитания Пример сложения «столбиком» (1410 + 510 = 1910 или 11102 + 1012 = 100112): Таблица умножения Пример умножения «столбиком» (1410 * 510 = 7010 или 11102 * 1012 = 10001102): Эти операции работают с целочисленными типами данных Таблица истинности побитовых операций выглядит следующим образом Представление отрицательных чисел в Java. Для хранения отрицательных чисел используется дополнительный код или второе дополнение (two’s complement). Положительное число преобразуется в отрицательное число путём инвертирования его бит с добавлением единицы. Пример: Преобразование 32-битного числа 5 = 101: Исходное число: 0000 0000 0000 0000 0000 0000 0000 0101 Знаковый сдвиг влево ( >) Сдвигает двоичное представление первого операнда вправо на количество бит, заданное во втором операнде, знак числа сохраняется. Старшие(крайние левые биты) заполняются нулями. Соответствует делению на 2: Беззнаковый сдвиг вправо(>>>) Сдвигает двоичное представление первого операнда вправо на количество бит, заданное во втором операнде, знак числа не сохраняется. Для положительных чисел работает как деление: 24 (11000) >>> 1 = 12 (1100) Можно увидеть, что знаковый бит был заменён нулём Особенности работы операторов сдвига Операторы сдвига всегда возвращают тип int, даже если аргумент типа, например, byte. поэтому следующий код вернёт ошибку: Примеры применения битовых операций Задача 1: Пусть у нас есть A и B. Необходимо поменять их местами без использования дополнительной переменной. A = A + B В этом решении есть большой минус: возможность переполнения. Поэтому лучше использовать поразрядную операцию XOR. A = A ^ B Как это работает: в первой строке мы получаем маску на различающиеся биты, в этих разрядах будут стоять единички. Далее производится сброс и выставление нужных бит для обмена значений. Рассмотрим обмен чисел 5 и 9. A = 0101 ^ 1001 = 1100 Задача 2: Даны два числа K, N. Необходимо вычислить арифметическое выражение вида: K * 2^N, используя только битовые операции. Вывод: результат выражения K * 2^N Пример: K = 3, N = 4 Ответ: 48 Реализация: Сдвиг вправо >> 0110 => 0011 Побитовое или ︳ 0011
——- => 1011
1011Побитовое и & 0011
——- => 1011
1011Побитовое отрицание 0011 => 1100 Побитовое исключающее ИЛИ (то же, что ноль, но отличается от единицы) ^ 0011
——- => 1000
1011100: преобразование цвета
101: Перечисление
110: шифрование
111: Другие приложения
IT1300: Императивное программирование
Что значит сдвинуть число на один двоичный разряд вправо
Представление отрицательных чисел
Операции сдвига
О битовых операциях
Авторизуйтесь
О битовых операциях
Введение
Побитовое ИЛИ (OR)
A 0 0 1 0 0 1 1 0 B 0 0 1 1 0 1 0 1 A | B 0 0 1 1 0 1 1 1 Побитовое И (AND)
A 0 0 1 0 0 1 1 0 B 0 0 1 1 0 1 0 1 A & B 0 0 1 0 0 1 0 0 Исключающее ИЛИ (XOR)
A 1 0 0 0 1 0 1 0 B 0 0 1 0 1 0 1 1 A ^ B 1 0 1 0 0 0 0 1 Побитовое отрицание (NOT)
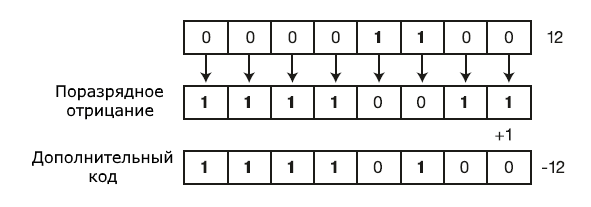
Дополнительный код
A 0 1 1 0 1 1 0 1 1 0 0 1 0 0 1 1 Побитовый сдвиг влево
Побитовый сдвиг вправо
Вывод
Что значит сдвинуть число на один двоичный разряд вправо
+ 0 1 0 0 1 1 1 10(перенос
в старший
разряд)— 0 1 0 0 д 1 (заём из
старшего
разряда) 10 + 1 1 1 0 1 0 1 1 0 0 1 1 × 0 1 0 0 0 1 0 1 × 1 1 1 0 1 0 1 + 1 1 1 0 1 1 1 0 1 0 0 0 1 1 0 A B A & B A | B A ^ B 1 0 0 1 1 0 1 0 1 1 1 1 1 1 0 0 0 0 0 0
Инвертируем: 1111 1111 1111 1111 1111 1111 1111 1010
Прибавляем 1: 0000 0000 0000 0000 0000 0000 0000 0001
Результат: 1111 1111 1111 1111 1111 1111 1111 1011
-24 (1111 1111 1111 1111 1111 1111 1110 1000) >>> 1 = 2147483636 (0111 1111 1111 1111 1111 1111 1111 0100)
B = A – B // После этого B становится A, т.к. в действительности получаем (A + B) – B = A
A = A – B
B = A ^ B
A = A ^ B
B = 1100 ^ 1001 = 0101
A = 1100 ^ 0101 = 1001
Умножение числа на 2 в степени N эквивалентно сдвигу влево на N позиций.
K