Что значит решить уравнение определение
Что такое уравнение: определение, решение, примеры
В данной публикации мы рассмотрим, что такое уравнение, а также, что значит его решить. Представленная теоретическая информация сопровождается практическими примерами для лучшего понимания.
Определение уравнения
Уравнение – это равенство, содержащее неизвестное число, которе требуется найти.
Другими словами, равенство является уравнением только в том случае, когда содержит букву, значение которой требуется вычислить.
Примеры простейших уравнений (одна неизвестная и одно арифметическое действие):
В более сложных уравнениях переменная может встречаться несколько раз, также, в них могут содержаться скобки и более сложные математические операции. Например:
Также, в уравнении может быть несколько переменных, например:
Корень уравнения
Решить уравнение – это значит найти его корень или корни (в зависимости от количества переменных), либо доказать, что их нет.
Примечания:
1. Некоторые уравнения могут быть не решаемы.
2. Некоторые уравнения имеют бесконечное множество корней.
Равносильные уравнения
Уравнения, имеющие одни и те же корни, называются равносильными.
Основные равносильные преобразования уравнений:
1. Перенос какого-то слагаемого из одной части уравнений в другую с изменением его знака на противоположный.
2. Умножение/разделение обеих частей уравнения на одно и то же число, не равное нулю.
Уравнение, также, не изменится, если к обеим его частям прибавить/отнять одно и то же число.
3. Приведение подобных слагаемых.
Решение простых линейных уравнений
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.
В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении: Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа. Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством. Числовой коэффициент — число, которое стоит при неизвестной переменной. Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз: Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем. Как решать простые уравненияЧтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила. 1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный. Для примера рассмотрим простейшее уравнение: x+3=5 Начнем с того, что в каждом уравнении есть левая и правая часть. Перенесем 3 из левой части в правую и меняем знак на противоположный. Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2. Решим еще один пример: 6x = 5x + 10. Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус. Приведем подобные и завершим решение. 2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок. Применим правило при решении примера: 4x=8. При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение. Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица. Разделим каждую часть на 4. Как это выглядит: Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения: Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12 Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах. Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные. Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки. Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе. А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе. Примеры линейных уравненийТеперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе! Пример 1. Как правильно решить уравнение: 6х + 1 = 19. Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1. 5х — 15 + 2 = 3х — 2 + 2х — 1 Ответ: х — любое число. Пример 3. Решить: 4х = 1/8. Пример 4. Решить: 4(х + 2) = 6 — 7х. Пример 5. Решить: Пример 6. Как решить линейное уравнение: х + 7 = х + 4. 5х — 15 + 2 = 3х — 2 + 2х — 1 Пример 7. Решить: 2(х + 3) = 5 — 7х.. Содержание: Выражения и уравненияВы уже знаете, что такое буквенные выражения, и умеете их упрощать с помощью законов сложения и умножения. Например, Пример: Есть ли коэффициент в выражении Вспомним, что преобразование выражения со скобками в выражение без скобок называется раскрытием скобок. Например: Обратным действием в этом примере является вынесение общего множителя за скобки. Слагаемые, содержащие одинаковые буквенные множители, называют подобными слагаемыми. С помощью вынесения общего множителя за скобки сводят подобные слагаемые: Правила раскрытия скобокПравила раскрытия скобок Пример: Упростите выражение: 1) Решение: 1. Перед скобками стоит знак 2. Перед скобками стоит знак Для раскрытия скобок используют распределительное свойство умножения: Пример: Упростите выражение: 1) Решение: 1. Множитель 2. Множитель Уравнения. Основные свойства уравненийВы уже знаете, что такое уравнение, корень уравнения. Вспомним основные формулировки. Определение: Уравнением называется равенство, содержащее неизвестное, значение которого нужно найти. Неизвестное число в уравнении обозначают буквой уравнением, где Определение: Значение неизвестного, обращающее уравнение в верное числовое равенство, называется корнем уравнения. Так, корнем уравнения Уравнение может иметь больше одного корня. Например, уравнение Уравнение может не иметь корней. Например, уравнение Определение: Решить уравнение — значит найти все его корни или установить, что уравнение не имеет ни одного корня. В 5 классе вы находили корень уравнения как неизвестный компонент арифметического действия. При решении более сложных уравнений опираются на свойства равенств. Рассмотрим основные из них. Посмотрите на рисунок 139. Вы видите, что на левой чаше весов находится арбуз неизвестной массы, а на правой — гири массой 5 кг и 3 кг. Если на обе чаши весов положить по гире массой 3 кг, то весы останутся в равновесии (рис. 140). Понятно, что, сняв эти гири или поставив навесы одинаковые гири другой массы, снова получим равновесие на весах. Этот пример иллюстрирует следующее свойство равенств. Определение: Если к обеим частям равенства прибавить (из обеих частей равенства вычесть) одно и то же число, то равенство не изменится. Пример: Решите уравнение: 1) Решение: К левой и правой частям уравнения прибавим число 12 и упростим полученное равенство: Решая уравнение, в левой его части «уединили неизвестное». Такой же результат получим, если число 12 перенесём из левой части в правую, изменив при этом его знак. Определение: Слагаемое можно переносить из одной части уравнения в другую, изменяя знак этого слагаемого на противоположный. Пример: Можно ли переносить в другую часть уравнения слагаемое, содержащее неизвестное? Да. Посмотрите на рисунок 141. Вы видите, что масса пакета муки равна 2 кг. Понятно, что масса трёх таких пакетов втрое больше (рис. 142). Этот пример иллюстрирует другое свойство равенств. Определение: Если обе части равенства умножить (разделить) на одно и то же число, отличное от нуля, то равенство не изменится. Пример: Решите уравнение Решение: Чтобы избавиться от дробного коэффициента, умножим на 3 обе части уравнения: Основные свойства уравненийОсновные свойства уравнений Считают, что язык алгебры — это уравнения. «Чтобы решить вопросы. относящиеся к числам или к абстрактным отношениям величин, нужно лишь перевести задачу с родного языка на язык алгебраический», — писал великий И. Ньютон (1643-1727) в своём учебнике по алгебре, названном «Общая арифметика». Применение уравнений к решению задачВ 5 классе с помощью уравнений вы решали задачи на нахождение суммы двух величин или их разности. В 6 классе будем рассматривать особый вид задач — на равенство двух величин. В таких задачах тоже сравнивают две величины, например, количество книг на первой и второй полках. Значения же выражений с этими двумя величинами приравнивают. Пример: На первой полке книг в 3 раза больше, чем на второй. Если с первой полки переставить на вторую 12 книг, то на обеих полках их станет поровну. Сколько книг на каждой полке? Решение: Составим краткую запись задачи в виде таблицы 23 Пусть Первым произведением, содержащим исследование алгебраических вопросов, считают трактат «Арифметика» Диофанта (середина IV в.). Из 13 книг, составляющих полное собрание трудов Диофанта, до нас дошло только 6. В них предложено решение сложных алгебраических задач. Основная часть трактата — сборник задач (в первых шести книгах их 189) с решениями и удачно подобранными иллюстрациями к способам решения. Перпендикулярные и параллельные прямыеВы знаете, что прямая — это геометрическая фигура. Две прямые могут по-разному размещаться на плоскости. В 6 классе вы узнаете о перпендикулярных и параллельных прямых. Перпендикулярные прямыеПосмотрите па перекрёсток дорог на рисунке 143. Вы видите, что дороги напоминают пересекающиеся прямые, которые образуют четыре прямых угла. В этом случае говорят, что прямые пересекаются под прямым углом. В тетради по математике клеточки образуются перпендикулярными прямыми. Определение: Две прямые на плоскости называются перпендикулярными, если они пересекаются под прямым углом. На рисунке 144 изображены прямые
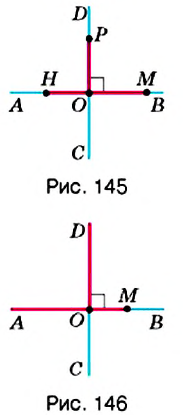
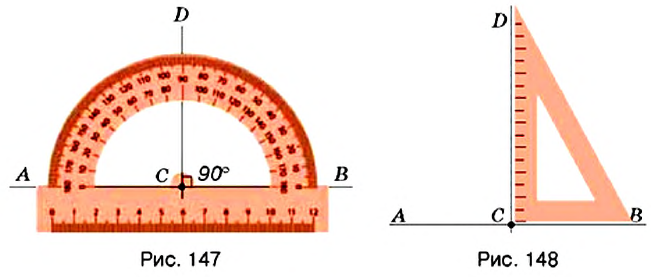
Если прямая Пример: Бывают ли перпендикулярными отрезки? лучи? Да, если они являются частями соответствующих перпендикулярных прямых (рис. 145—146). Для построения перпендикулярных прямых используют транспортир или угольник. На рисунке 147 вы видите, как строили прямую Параллельные прямыеПосмотрите на рисунок 149. Вы видите рельсы трамвайных путей, напоминающие прямые, которые лежат в одной плоскости и не пересекаются. Это пример параллельных прямых. Вокруг нас много других примеров параллельных прямых. Так, в тетради в клеточку горизонтальные линии параллельны. То же самое можно сказать и про вертикальные линии. Противоположные края парты, противоположные стороны оконной рамы, троллейбусные штанги также параллельны. Определение: Две прямые на плоскости называются параллельными, если они не пересекаются. На рисунке 150 изображены параллельные прямые
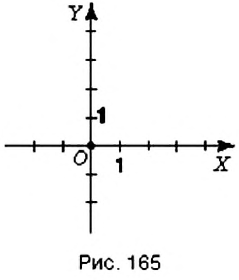
Если прямая Пример: Бывают ли параллельными лучи? отрезки? Да, если они являются частями соответствующих параллельных прямых. На рисунке 151 вы видите, как с помощью линейки и угольника через точку Название «перпендикулярный» происходит от латинского слова «perpendicufaris», которое означает «отвесный». Знак Название «параллельный» происходит от греческого слова «раralelos» — «идущий рядом». Символ параллельности Координатная плоскостьВы уже знаете, что такое координатная прямая (рис. 162). На ней точка Однако на практике часто приходится пользоваться ориентирами не только вдоль прямой, но и на плоскости. Вы знаете, что в игре «Морской бой» положение корабля определяют с помощью «координат» из цифр и «координат» из букв (рис. 163). В зависимости от выбранной буквы передвигаются на определённое количество клеточек вправо или влево, а цифра указывает, на сколько клеточек нужно сместиться вверх или вниз. Итак, место корабля на поле боя определяют двумя « координатами». Чтобы определить место в зале кинотеатра, также нужно знать две «координаты»: номер ряда и номер кресла в этом ряду (рис. 164). Причём порядок «координат» в такой паре является строго определённым. Действительно, например, пары чисел 3 и 12 и 12 и 3 направят нас в совершенно разные места зала: в 3-й ряд на 12-е место или в 12-й ряд на 3-е место. В отличие от предыдущего примера, для ориентирования в зале кинотеатра порядок координат не меняют, поскольку неудобно сначала искать номер места в ряду, а лишь затем — сам ряд. Итак, чтобы охарактеризовать размещение точки на плоскости, нужно задать две координатные прямые с равными единичными отрезками, одна из которых задаёт направление вправо-влево, а вторая — вверх-вниз. Для этого координатные прямые изображают перпендикулярно друг к другу и так, чтобы начала отсчёта на них совпадали (рис. 165). Одну из этих прямых (как правило, горизонтальную) считают первой, а другую — второй. Такая пара координатных прямых образует прямоугольную систему координат. Первую координатную прямую называют осью абсцисс. Её обозначают Плоскость с заданной на ней системой координат называют координатной плоскостью. Каждой точке на плоскости можно поставить в соответствие пару чисел, взятых в определённом порядке, и наоборот, каждой паре чисел соответствует единственная точка координатной плоскости. Такая упорядоченная пара чисел называется координатами точки в данной системе координат. Координату по оси абсцисс называется абсциссой точки, а координату по оси ординат — ординатой точки.
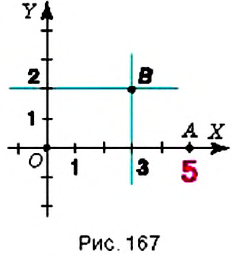
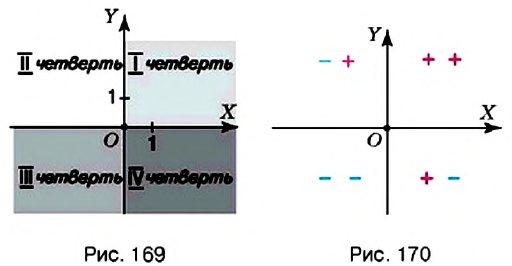
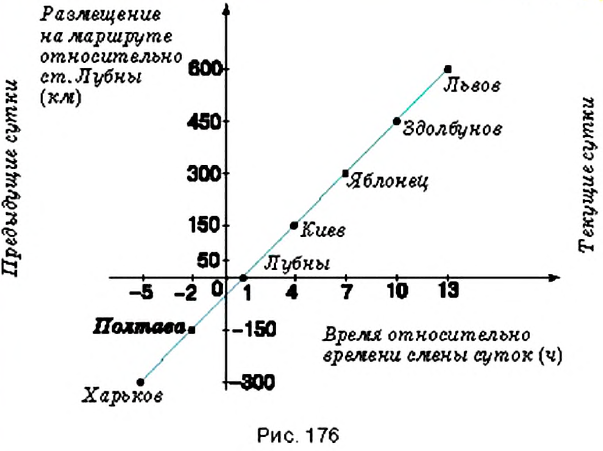
Пример: На координатной плоскости постройте точку: 1) Решение: Введём прямоугольную систему координат на плоскости (рис. 167). 1. У точки 2. Поскольку ордината точки Обратите внимание: Пример: Координатные оси разбивают координатную плоскость на четыре части. Их называют координатными четвертями и обозначают так: I четверть, II четверть, III четверть, IV четверть (рис. 169). Точки I четверти имеют положительную абсциссу и положительную ординату. И наоборот, если абсцисса и ордината точки положительные, то она лежит в I четверти, как, например, точка На рисунке 170 показаны знаки координат точек, лежащих в соответствующих четвертях. Положение любой точки на поверхности Земли определяется двумя координатами: географической широтой и географической долготой. Географические координаты ввёл древнегреческий учёный Гиппарх во И в. до н.э. Географические координаты применяют для определения положения точек земной поверхности относительно экватора и начального (нулевого) меридиана. Например, Киев имеет следующие географические координаты: Графики зависимостей между величинамиВы знаете, что стоимость товара зависит от его количества: чем большее количество товара покупают, тем большей будет его стоимость. Например, если цена одного килограмма конфет составляет 35 грн, то за 2 кг нужно заплатить 70 грн, за 3 кг — 105 грн и т.п. Вы знаете, что такое соответствие можно наглядно отобразить на диаграмме (рис. 174). Однако по диаграмме трудно определить, сколько стоит 2,5 кг конфет или иное их количество. Изобразим данные о стоимости конфет не в виде столбиков, а вертикальными отрезками в системе координат (рис. 175). Поскольку величины «масса конфет» и «стоимость покупки» являются прямо пропорциональными, то верхние концы столбиков диаграммы можно соединить отрезками. Получим линию, показывающую, как изменяется стоимость покупки в зависимости от массы конфет. Такая линия называется графиком зависимости величины «стоимость покупки» от величины «масса конфет». Обратите внимание: все точки графика зависимости прямо пропорциональных величин лежат на одной прямой. Вы знаете, что расстояние и время на его преодоление являются прямо пропорциональными величинами. Поэтому все точки графика движения лежат на одной прямой. Пример: Поезд Харьков — Львов выходит из Харькова около 1) В котором часу новых суток поезд делает первую остановку? Какая это станция? 2) Что показывает число 3) На каких расстояниях от первой остановки поезд останавливается на других станциях? 4) Что показывает число 5) Каковы координаты конечных точек маршрута? Решение: По условию задачи, движение поезда начинается в 1. Начало новых суток поезд встречает недалеко от станции Лубны, а первую остановку делает в 2. Поскольку движение поезда началось в предыдущие сутки, то по оси абсцисс время его отправления из Харькова можно выразить отрицательным числом 3. Остановки запланированы через каждые 4. При помощи отрицательных чисел 5. Конечные результаты точки маршрута поезда имеют координаты Пример: Обязательно ли выбирать конечные точки маршрута для построения графика движения? Нет. График можно построить по любым двум его точкам. Но концы маршрута нужно отметить обязательно. Обратите внимание: график движения является прямой (или её частью), поэтому такой график можно построить по любым двум его точкам. С помощью графиков можно решать целый класс задач. Рассмотрим задачу. Пример: Из пунктов Решение: Построим в прямоугольной системе координат графики движения автомобилей (рис. 177). Красный отрезок — график движения красного автомобиля, синий — синего автомобиля. Точке пересечения этих отрезков соответствует время — 9 ч. Итак, автомобили встречаются в 9 ч. При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
|
|---|



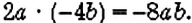
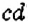 ? Да. Он равен 1, поскольку
? Да. Он равен 1, поскольку 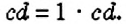
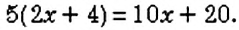
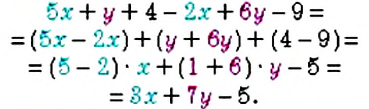
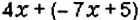 ; 2)
; 2)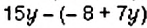
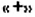 , поэтому при раскрытии скобок знаки всех слагаемых сохраняются:
, поэтому при раскрытии скобок знаки всех слагаемых сохраняются: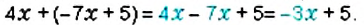
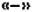 , поэтому при раскрытии скобок знаки всех слагаемых изменяются на противоположные:
, поэтому при раскрытии скобок знаки всех слагаемых изменяются на противоположные: 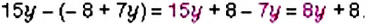
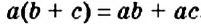 . Если
. Если 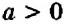 , то знаки слагаемых
, то знаки слагаемых 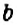 и
и 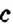 не изменяют. Если
не изменяют. Если 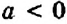 , то знаки слагаемых
, то знаки слагаемых 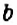 и
и 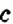 изменяют на противоположные.
изменяют на противоположные.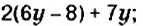 2)
2) 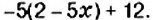
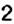 перед скобками является положительным, поэтому при раскрытии скобок знаки всех слагаемых сохраняем:
перед скобками является положительным, поэтому при раскрытии скобок знаки всех слагаемых сохраняем: 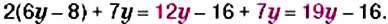
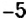 перед скобками является отрицательным, поэтому при раскрытии скобок знаки всех слагаемых изменяем на противоположные:
перед скобками является отрицательным, поэтому при раскрытии скобок знаки всех слагаемых изменяем на противоположные: 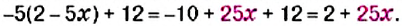

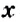 или
или 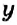 , или
, или 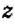 и т.п. Например, запись
и т.п. Например, запись 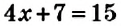 является
является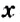 — неизвестное и является искомым.
— неизвестное и является искомым.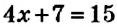 является число
является число 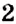 , поскольку
, поскольку 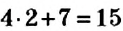 .
.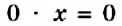 имеет бесконечно много корней, так как любое число обращает уравнение в верное числовое равенство. С уравнениями, имеющими два, три или более корней, вы ознакомитесь позднее.
имеет бесконечно много корней, так как любое число обращает уравнение в верное числовое равенство. С уравнениями, имеющими два, три или более корней, вы ознакомитесь позднее.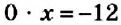 не имеет корней, так как не существует числа, которое в произведении с числом
не имеет корней, так как не существует числа, которое в произведении с числом 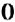 даёт число
даёт число 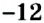 .
.
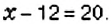 .
.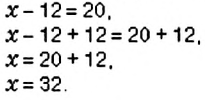
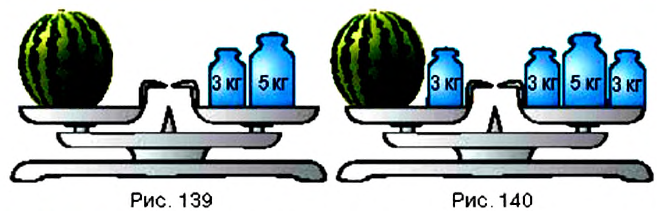
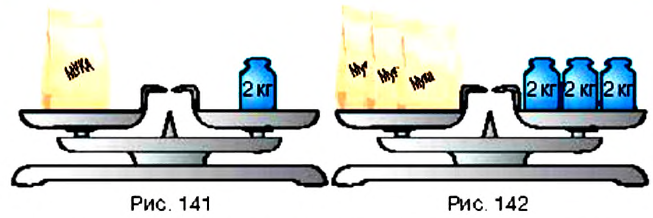 Данное свойство используют для решения уравнений. Рассмотрим пример.
Данное свойство используют для решения уравнений. Рассмотрим пример.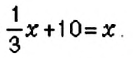
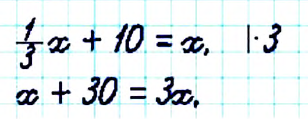
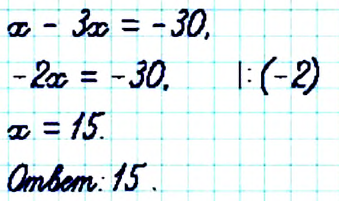
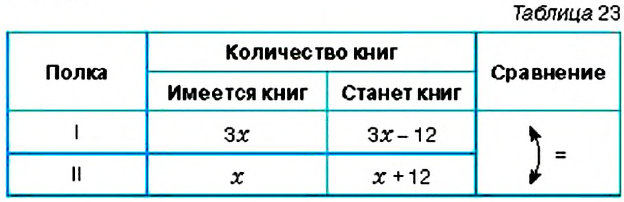
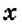 — количество книг на второй полке, тогда
— количество книг на второй полке, тогда 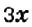 — количество книг на первой полке. Если с первой полки переставить на вторую 12 книг, то на первой полке их станет
— количество книг на первой полке. Если с первой полки переставить на вторую 12 книг, то на первой полке их станет 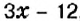 , а на второй —
, а на второй — 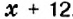 . По условию, это количество книг одинаково. Составим уравнение:
. По условию, это количество книг одинаково. Составим уравнение: 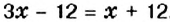 . Решим уравнение:
. Решим уравнение: 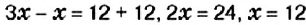 . Тогда
. Тогда  . Следовательно, на первой полке 36 книг, а на второй — 12 книг.
. Следовательно, на первой полке 36 книг, а на второй — 12 книг.

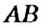 и
и 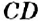 , которые пересекаются в точке О под прямым углом, то есть являются перпендикулярными.
, которые пересекаются в точке О под прямым углом, то есть являются перпендикулярными. Записывают:
Записывают: 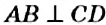 , а на рисунке обозначают знаком прямого угла
, а на рисунке обозначают знаком прямого угла 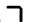 (см. рис. 145). Говорят: «Прямая
(см. рис. 145). Говорят: «Прямая 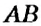 перпендикулярна прямой
перпендикулярна прямой 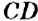 ».
».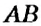 перпендикулярна прямой
перпендикулярна прямой 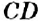 , то и прямая
, то и прямая  перпендикулярна прямой
перпендикулярна прямой 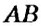 . Иначе говорят: прямые
. Иначе говорят: прямые 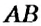 и
и 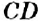 — взаимно перпендикулярны.
— взаимно перпендикулярны.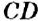 , перпендикулярную прямой
, перпендикулярную прямой  , с помощью транспортира, а на рисунке рис. 148 — с помощью угольника.
, с помощью транспортира, а на рисунке рис. 148 — с помощью угольника.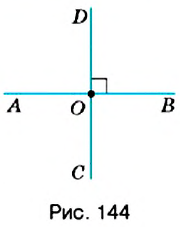

 Записывают:
Записывают: 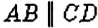 . Говорят: «Прямая
. Говорят: «Прямая 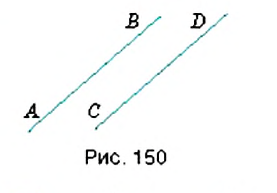
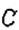 провели прямую
провели прямую 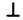 предложил Пьер Еригон (1580—1643) — французский математик и астроном.
предложил Пьер Еригон (1580—1643) — французский математик и астроном.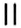 известен с античных времён Его использовали Герои и Папп Александрийский. Сначала символ был похож на нынешний знак равенства, но с появлением последнего, чтобы избежать путаницы, символ был повёрнут вертикально Уильямом Отредом в 1677 году
известен с античных времён Его использовали Герои и Папп Александрийский. Сначала символ был похож на нынешний знак равенства, но с появлением последнего, чтобы избежать путаницы, символ был повёрнут вертикально Уильямом Отредом в 1677 году — начало отсчёта, стрелка показывает направление возрастания чисел, а цена деления составляет одну единицу.
— начало отсчёта, стрелка показывает направление возрастания чисел, а цена деления составляет одну единицу.
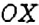 . Вторую координатную прямую называют осью ординат. Её обозначают
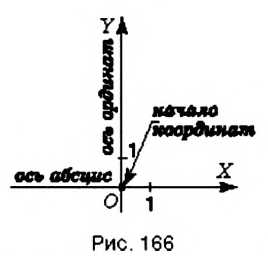
. Вторую координатную прямую называют осью ординат. Её обозначают 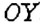 . Общее начало отсчёта координатных прямых называют началом координат (рис. 166).
. Общее начало отсчёта координатных прямых называют началом координат (рис. 166).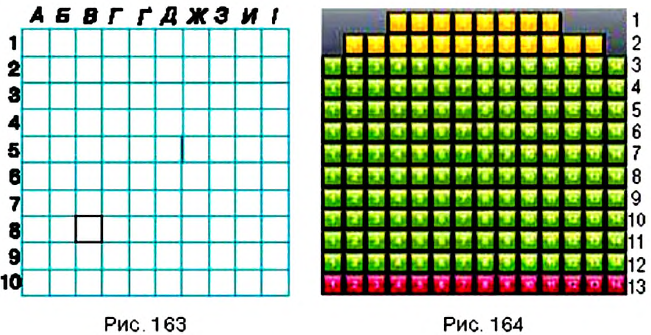
 Кратко записывают:
Кратко записывают: 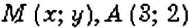 . Читают: «Точка
. Читают: «Точка 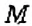 с координатами
с координатами 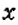 и
и 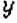 », «Точка
», «Точка 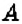 с координатами 3 и 2» или «3 — абсцисса точки
с координатами 3 и 2» или «3 — абсцисса точки 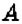 , 2 — её ордината».
, 2 — её ордината».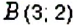 ; 2)
; 2) 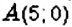 .
.
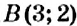 . Аналогично рассуждая, можно выяснить, что точки II четверти имеют отрицательную абсциссу и положительную ординату, точки III четверти — отрицательную абсциссу и отрицательную ординату, а точки IV четверти — положительную абсциссу и отрицательную ординату.
. Аналогично рассуждая, можно выяснить, что точки II четверти имеют отрицательную абсциссу и положительную ординату, точки III четверти — отрицательную абсциссу и отрицательную ординату, а точки IV четверти — положительную абсциссу и отрицательную ординату.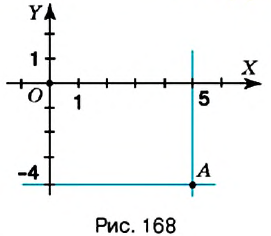
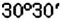 восточной долготы,
восточной долготы, 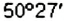 северной широты.
северной широты.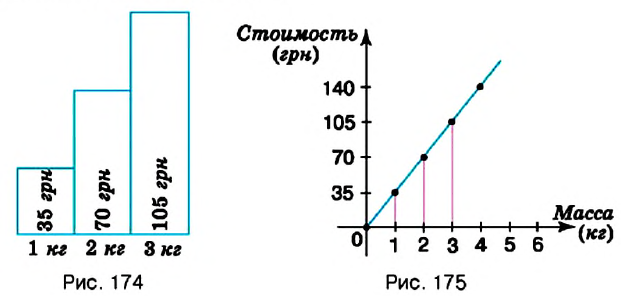
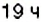 и прибывает во Львов около
и прибывает во Львов около 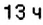 . Скорость поезда составляет
. Скорость поезда составляет 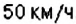 , на маршруте он делает 5 остановок, запланированных через каждые 3 часа. На рисунке 176 показан график движения этого поезда.
, на маршруте он делает 5 остановок, запланированных через каждые 3 часа. На рисунке 176 показан график движения этого поезда.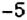 на оси абсцисс? А число
на оси абсцисс? А число 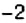 ?
?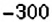 на оси ординат? А число
на оси ординат? А число 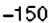 ?
?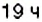 , а заканчивается в
, а заканчивается в 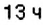 следующего дня.
следующего дня.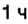 именно на этой станции.
именно на этой станции.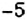 . Действительно, в
. Действительно, в 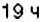 предыдущих суток до начала новых суток должно пройти именно
предыдущих суток до начала новых суток должно пройти именно 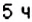 . Аналогично, времени остановки поезда в Полтаве на оси абсцисс соответствует отрицательное число
. Аналогично, времени остановки поезда в Полтаве на оси абсцисс соответствует отрицательное число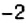 .
.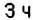 . Поскольку скорость поезда составляет
. Поскольку скорость поезда составляет 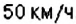 , то за
, то за 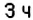 он преодолевает
он преодолевает 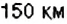 . Следовательно, поезд останавливается на таких расстояниях от Полтавы:
. Следовательно, поезд останавливается на таких расстояниях от Полтавы: 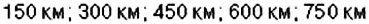 .
.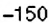 на оси ординат показано, что в
на оси ординат показано, что в 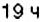 предыдущих суток поезд находился на расстоянии 300 км. не доезжая до станции Лубны, а в
предыдущих суток поезд находился на расстоянии 300 км. не доезжая до станции Лубны, а в 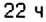 предыдущих суток — на расстоянии
предыдущих суток — на расстоянии 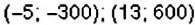 .
.
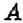 и
и 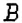 , расстояние между которыми составляет 420 км. навстречу друг другу выехали два автомобиля. Красный автомобиль выехал в 6 ч из пункта
, расстояние между которыми составляет 420 км. навстречу друг другу выехали два автомобиля. Красный автомобиль выехал в 6 ч из пункта 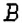 в 15 ч. Синий автомобиль выехал в 5 ч из пункта
в 15 ч. Синий автомобиль выехал в 5 ч из пункта  и прибыл в пункт
и прибыл в пункт