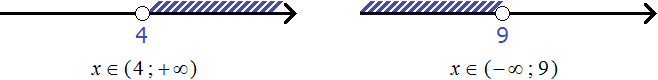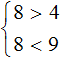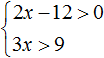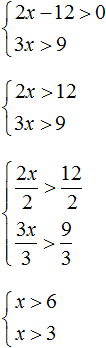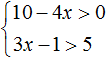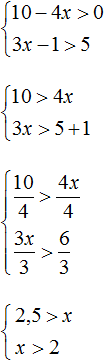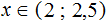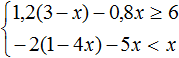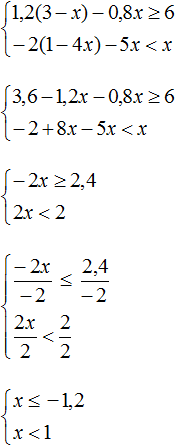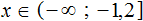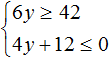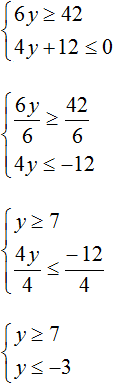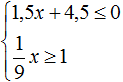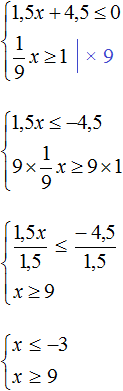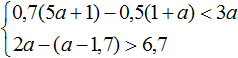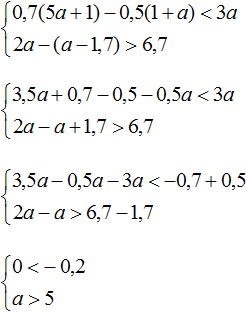Что значит решить систему уравнений неравенств
Неравенство. Система линейных неравенств.
Системой линейных неравенств называется любая совокупность двух или более линейных неравенств, содержащих одну и туже неизвестную величину
Вот образцы подобных систем:
Решить систему неравенств означает установить все значения неизвестной величины, при которых реализуются все неравенство системы, либо доказать, что таких не существует.
Все решения системы неравенств формируют множество решений. Если система неравенств не реализуется ни при каких значениях х, то обозначают, что такие системы неравенств несовместимы.
Установим область определения функции 
.
Область определения или область допустимых значений –это множество всех х при которых функция существует.
Функция существует, когда существуют оба квадратных корня, т.е. под корнем стоит не отрицательное число.
Как рассчитать такую систему? Следует установить все x, одновременно выполняющие условия и первого и второго неравенства.
Воспроизведем на оси x множество решений первого и второго неравенства.
Промежуток пересечения двух лучей и есть наше решение. Следовательно решением данного неравенства выступают все х расположенные между двойкой и восьмеркой.
Ответ: х
[2;8]
Применение такого типа отображения решения системы неравенств иногда именуют методом крыш.
Определение: Пересечением двух множеств А и В называется такое третье множество, которое включает все элементы, входящих и в А и в В. Это смысл пересечения множеств произвольной природы. Нами сейчас детально рассматриваются числовые множества, поэтому при нахождении линейных неравенств такими множествами являются лучи – сонаправленные, противонаправленные и так далее.
Выясним на реальных примерах нахождение линейных систем неравенств, как определить пересечения множеств решений отдельных неравенств, входящих в систему.
Вычислим систему неравенств:
1. 
Поместим одну под другой две силовые прямые. На верхней нанесем те значения х, которые выполняют первое неравенство x>7, а на нижней – которые выступают решением второго неравенства x>10 Соотнесем результаты числовых прямых, выясним, что оба неравенства будут удовлетворятся при x>10.
2. 
4.Решить систему
Откуда может взяться второе неравенство системы? Например, из неравенства x 2 + 1 ≥ 0,
Графически обозначим решения каждого неравенства и найдем промежуток их пересечения.
Таким образом, если мы имеем систему, в которой одно из неравенств удовлетворяет любому значению x, то его можно отбросить.
5.
Ответ:x
система противоречива.
Решение совокупностей неравенств с одной переменной
Понятие совокупности неравенств с одной переменной и его решения
Решением совокупности неравенств с одной переменной является такое множество значений этой переменной, которое превращает хотя бы одно из неравенств в верное числовое неравенство.
Алгоритм решения системы неравенств с одной переменной
Шаг 1. Найти множество решений для каждого из неравенств системы. Если какое-либо частное решение является пустым множеством, отбросить его, но продолжить решение.
Шаг 2. Начертить друг под другом числовые прямые, число которых равно числу полученных непустых частных решений. Начала отсчёта числовых прямых должны находиться на общем перпендикуляре, единичный отрезок должен совпадать.
Шаг 3. На числовых прямых изобразить полученные частные решения, на отдельной прямой найти их объединение – это и будет общим решением системы.
Шаг 4. Работа завершена.
Сравнение систем и совокупностей неравенств
$\left[ \begin
Объединение частных решений
Вся система не имеет решений
(аналогия с умножением на 0)
Вся совокупность может иметь
(аналогия с прибавлением 0)
Неравенства могут образовывать сложные конструкции условий из вложенных систем и совокупностей. Раскрытие скобок при упрощении таких конструкций подчиняется законам логики и правилам операций над множествами (см. §10 данного справочника).
Примеры
Пример 1. Решите совокупности уравнений:
Пример 2. Решите неравенство:
Произведение слева будет отрицательным, если сомножители будут иметь разные знаки. Получаем совокупность двух систем неравенств:
Произведение слева будет положительным (или равным 0), если сомножители будут иметь одинаковые знаки (или равными 0).
Получаем совокупность двух систем неравенств:
Для нижнего неравенства получаем совокупность:
Возвращаемся к исходной переменной
В 9 классе для решения подобных неравенств будет предложен очень эффективный метод интервалов, который позволяет значительно упростить ход решения.
Системы линейных неравенств с одной переменной
Примеры решения систем линейных неравенств с одной переменной
Несколько линейных неравенств, удовлетворяющих одним и тем же решениям, образуют систему.
Рассмотрим простейший пример. Система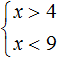 
состоит из двух неравенств, которые уже решены.
Решениями первого неравенства являются все числа, которые больше 4. Решениями второго неравенства являются все числа, которые меньше 9.
Изобразим множество решений каждого неравенства на координатной прямой и запишем ответы к ним в виде числовых промежутков:
Но дело в том, что неравенства x > 4 и x соединены знаком системы, а значит зависимы друг от друга. Им не дозволяется раскидываться решениями, как захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму.
Говоря по-простому, нужно указать числа, которые больше 4, но меньше 9. Очевидно, что речь идет о числах, находящихся в промежутке от 4 до 9.
Значит решениями системы 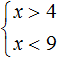являются числа от 4 до 9. Границы 4 и 9 не включаются во множество решений системы, поскольку неравенства x > 4 и x строгие. Ответ можно записать в виде числового промежутка:
Также, нужно изобразить множество решений системы на координатной прямой.
Для системы линейных неравенств решение на координатной прямой изображают так:
Сначала указывают границы обоих неравенств:
На верхней области отмечают множество решений первого неравенства x > 4
Видим, что решение 8 удовлетворяет обоим неравенствам.
Исходя из рассмотренного примера, можно сформировать правило для решения системы линейных неравенств:
Чтобы решить систему линейных неравенств, нужно по отдельности решить каждое неравенство, и указать в виде числового промежутка множество решений, удовлетворяющих каждому неравенству.
Пример 2. Решить систему неравенств 
Решениями первого неравенства являются все числа, которые больше 17. Решениями второго неравенства являются все числа, которые больше 12.
Решениями же обоих неравенств являются все числа, которые больше 17.
Изобразим множество решений системы 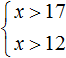на координатной прямой и запишем ответ в виде числового промежутка.
Для начала отметим на координатной прямой границы обоих неравенств:
На верхней области отметим множество решений первого неравенства x > 17
На нижней области отметим множество решений второго неравенства x > 12
Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы 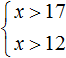. Видно, что эта область располагается в промежутке от 17 до плюс бесконечности. Запишем ответ в виде числового промежутка:
Пример 3. Решить систему неравенств 
Решим каждое неравенство по отдельности. Делать это можно внутри системы. Если испытываете затруднения при решении каждого неравенства, обязательно изучите предыдущий урок
Получили систему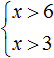 
. На этом решение завершается. Осталось изобразить множество решений системы на координатной прямой и записать ответ в виде числового промежутка.
Как и в прошлом примере, сначала нужно отметить границы обоих неравенств, затем отметить множество решений каждого неравенства ( x > 6 и x > 3 ). Область координатной прямой, отмеченная с обеих сторон, будет промежутком, в котором располагается множество решений системы
Пример 4. Решить систему неравенств 
Решим каждое неравенство по отдельности:
Изобразим множество решений системы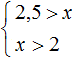 
на координатной прямой и запишем ответ в виде числового промежутка:
Пример 5. Решить неравенство 
Решим каждое неравенство по отдельности:
Изобразим множество решений системы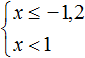 
на координатной прямой и запишем ответ в виде числового промежутка:
Когда решений нет
Если неравенства, входящие в систему, не имеют общих решений, то говорят, что система не имеет решений.
Пример 1. Решить неравенство 
Решим каждое неравенство по отдельности:
Решениями первого неравенства являются все числа, которые больше 7, включая число 7. Решениями второго неравенства являются все числа, которые меньше −3, включая число −3.
Видим, что у данных неравенств нет общих решений. Увидеть это наглядно позволит координатная прямая. Отметим на ней множество решений каждого неравенства:
На координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Это говорит о том, что неравенства y ≥ 7 и y ≤ −3 не имеют общих решений. Значит не имеет решений система 
А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система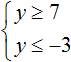
Ответ: решений нет.
Пример 2. Решить систему неравенств 
Решим каждое неравенство по отдельности:
Изобразим множество решений неравенств x ≤ −3 и x ≥ 9 на координатной прямой:
Видим, что на координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система 
А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система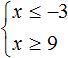
Ответ: решений нет.
Пример 3. Решить систему неравенств 
Решим каждое неравенство по отдельности:
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение систем неравенств: линейные, квадратные и дробные.
Программа для решения линейных, квадратных и дробных неравенств не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Причём, если в процессе решения одного из неравенств нужно решить, например, квадратное уравнение, то его подробное решение также выводится (оно заключается в спойлер).
Данная программа может быть полезна учащимся старших классов при подготовке к контрольным работам, родителям для контроля решения неравенств их детьми.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
В качестве переменной может выступать любая латинсая буква.
Например: \( x, y, z, a, b, c, o, p, q \) и т.д.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе выражений можно использовать скобки. В этом случае при решении неравенства выражения сначала упрощаются.
Например: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)
Выберите нужный знак неравенства и введите многочлены в поля ниже.
Решение системы неравенств
В данной публикации мы рассмотрим, что такое система линейных неравенств, как она решается методом интервалов на числовой оси. Также разберем практические примеры по этой теме.
Определение системы неравенств
Для решения системы неравенств необходимо иметь навыки, позволяющие справиться с линейными неравенствами. Мы подробно рассмотрели этот вопрос в отдельной публикации.
Система неравенств – это два или более неравенства, объединенные фигурной скобкой. Например:
Т.е. она чем-то похожа на систему уравнений, в которых “равно” заменено на один из знаков сравнения (“больше”, “меньше”, “больше или равно”, “меньше или равно”).
Примечание: в системе линейных неравенств все они, соответственно, являются линейными. Обычно неизвестная переменная в них всего одна (чаще всего обозначается как “x” ).
Решение системы линейных неравенств
Алгоритм состоит из двух основных шагов:
Пример 1
Давайте попробуем решить систему, приведенную выше.
Теперь отметим на числовой оси полученные результаты, разделив области решений разными цветами для удобства восприятия.
Нам нужен участок, где присутствуют оба решения. Как мы видим на рисунке, он начинается с числа 10 включительно.
Пример 2
Найдем решение системы неравенств ниже:
Перенесем найденные решения на числовую ось и нарисуем соответствующие им интервалы:
