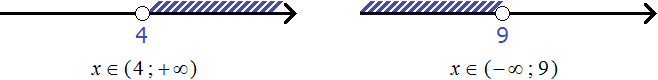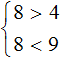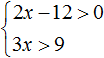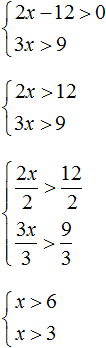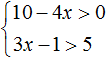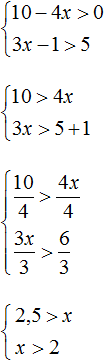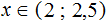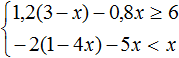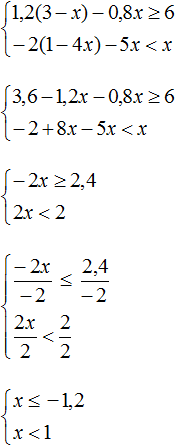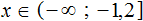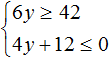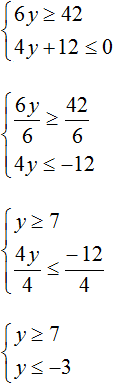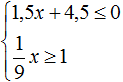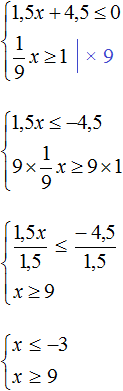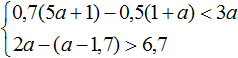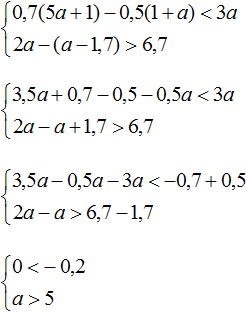Что значит решить систему линейных неравенств с одним неизвестным

Системы неравенств с одним неизвестным

Вы будете перенаправлены на Автор24

Система, которая содержит неравенства с одним неизвестным, еще называется системой линейных неравенств.

решения системы неравенств

С этой целью необходимо отдельно найти все возможные решения каждого из неравенств системы, а после отыскать общее решение, которое состоит из общей части всех найденных решений, т. е. все значения, входящие в каждое из этих решений.

Рассмотрим возможные варианты таких систем:

Решение системы: система решения не имеет, т.к. не существует таких чисел, которые одновременно меньше меньшего числа и больше большего числа.

Все четыре случая описывают все возможные варианты систем из двух неравенств с одним неизвестным и интуитивно понятны.

Часто для решения систем как двух, так и большего числа неравенства, используют числовую прямую, на которую наносят все решения каждого из неравенств системы, а затем ищут те значения, которые принадлежат каждому из решений. Найденные значения и являются решением заданной системы неравенств.

Найти решение системы:

Готовые работы на аналогичную тему

Легко получить или проверить данное решение, если нанести решение каждого неравенства на числовую прямую. Сразу станет очевидным общее решение системы.

Найти решение системы:

Мы получили 4-й вариант системы неравенств, при котором система решений не имеет.

Ответ: система решений не имеет.

Дробь будет отрицательной, если ее числитель и знаменатель будут иметь разные знаки. Составим два возможных варианта системы:

Решим первую систему:

Решим вторую систему:

Данная система решений не имеет.

При решении подобных примеров ошибочно составляют третью систему, которая состоит из решений первой и второй системы. Такой подход является грубой ошибкой, т.к. каждая из систем является самостоятельной и не зависит от другой.

Найти решение системы:

Найдем решение с помощью числовой прямой:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 03 07 2021

Источник

Неравенство. Система линейных неравенств.

Системой линейных неравенств называется любая совокупность двух или более линейных неравенств, содержащих одну и туже неизвестную величину

Вот образцы подобных систем:

Решить систему неравенств означает установить все значения неизвестной величины, при которых реализуются все неравенство системы, либо доказать, что таких не существует.

Все решения системы неравенств формируют множество решений. Если система неравенств не реализуется ни при каких значениях х, то обозначают, что такие системы неравенств несовместимы.

Установим область определения функции .

Область определения или область допустимых значений –это множество всех х при которых функция существует.

Функция существует, когда существуют оба квадратных корня, т.е. под корнем стоит не отрицательное число.

Как рассчитать такую систему? Следует установить все x, одновременно выполняющие условия и первого и второго неравенства.

Воспроизведем на оси x множество решений первого и второго неравенства.

Промежуток пересечения двух лучей и есть наше решение. Следовательно решением данного неравенства выступают все х расположенные между двойкой и восьмеркой.

Ответ: х[2;8]

Применение такого типа отображения решения системы неравенств иногда именуют методом крыш.

Определение: Пересечением двух множеств А и В называется такое третье множество, которое включает все элементы, входящих и в А и в В. Это смысл пересечения множеств произвольной природы. Нами сейчас детально рассматриваются числовые множества, поэтому при нахождении линейных неравенств такими множествами являются лучи – сонаправленные, противонаправленные и так далее.

Выясним на реальных примерах нахождение линейных систем неравенств, как определить пересечения множеств решений отдельных неравенств, входящих в систему.

Вычислим систему неравенств:

1.

Поместим одну под другой две силовые прямые. На верхней нанесем те значения х, которые выполняют первое неравенство x>7, а на нижней – которые выступают решением второго неравенства x>10 Соотнесем результаты числовых прямых, выясним, что оба неравенства будут удовлетворятся при x>10.

2.

4.Решить систему

Откуда может взяться второе неравенство системы? Например, из неравенства x 2 + 1 ≥ 0,

Графически обозначим решения каждого неравенства и найдем промежуток их пересечения.

Таким образом, если мы имеем систему, в которой одно из неравенств удовлетворяет любому значению x, то его можно отбросить.

5.

Ответ:x система противоречива.

Источник

Системы линейных неравенств с одной переменной

Примеры решения систем линейных неравенств с одной переменной

Несколько линейных неравенств, удовлетворяющих одним и тем же решениям, образуют систему.

Рассмотрим простейший пример. Система 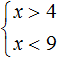состоит из двух неравенств, которые уже решены.

Решениями первого неравенства являются все числа, которые больше 4. Решениями второго неравенства являются все числа, которые меньше 9.

Изобразим множество решений каждого неравенства на координатной прямой и запишем ответы к ним в виде числовых промежутков:

Но дело в том, что неравенства x > 4 и x соединены знаком системы, а значит зависимы друг от друга. Им не дозволяется раскидываться решениями, как захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму.

Говоря по-простому, нужно указать числа, которые больше 4, но меньше 9. Очевидно, что речь идет о числах, находящихся в промежутке от 4 до 9.

Значит решениями системы 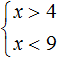являются числа от 4 до 9. Границы 4 и 9 не включаются во множество решений системы, поскольку неравенства x > 4 и x строгие. Ответ можно записать в виде числового промежутка:

Также, нужно изобразить множество решений системы на координатной прямой.

Для системы линейных неравенств решение на координатной прямой изображают так:

Сначала указывают границы обоих неравенств:

На верхней области отмечают множество решений первого неравенства x > 4

Видим, что решение 8 удовлетворяет обоим неравенствам.

Исходя из рассмотренного примера, можно сформировать правило для решения системы линейных неравенств:

Чтобы решить систему линейных неравенств, нужно по отдельности решить каждое неравенство, и указать в виде числового промежутка множество решений, удовлетворяющих каждому неравенству.

Пример 2. Решить систему неравенств

Решениями первого неравенства являются все числа, которые больше 17. Решениями второго неравенства являются все числа, которые больше 12.

Решениями же обоих неравенств являются все числа, которые больше 17.

Изобразим множество решений системы 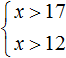на координатной прямой и запишем ответ в виде числового промежутка.

Для начала отметим на координатной прямой границы обоих неравенств:

На верхней области отметим множество решений первого неравенства x > 17

На нижней области отметим множество решений второго неравенства x > 12

Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы 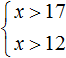. Видно, что эта область располагается в промежутке от 17 до плюс бесконечности. Запишем ответ в виде числового промежутка:

Пример 3. Решить систему неравенств

Решим каждое неравенство по отдельности. Делать это можно внутри системы. Если испытываете затруднения при решении каждого неравенства, обязательно изучите предыдущий урок

Получили систему 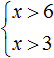. На этом решение завершается. Осталось изобразить множество решений системы на координатной прямой и записать ответ в виде числового промежутка.

Как и в прошлом примере, сначала нужно отметить границы обоих неравенств, затем отметить множество решений каждого неравенства ( x > 6 и x > 3 ). Область координатной прямой, отмеченная с обеих сторон, будет промежутком, в котором располагается множество решений системы

Пример 4. Решить систему неравенств

Решим каждое неравенство по отдельности:

Изобразим множество решений системы 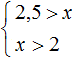на координатной прямой и запишем ответ в виде числового промежутка:

Пример 5. Решить неравенство

Решим каждое неравенство по отдельности:

Изобразим множество решений системы 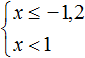на координатной прямой и запишем ответ в виде числового промежутка:

Когда решений нет

Если неравенства, входящие в систему, не имеют общих решений, то говорят, что система не имеет решений.

Пример 1. Решить неравенство

Решим каждое неравенство по отдельности:

Решениями первого неравенства являются все числа, которые больше 7, включая число 7. Решениями второго неравенства являются все числа, которые меньше −3, включая число −3.

Видим, что у данных неравенств нет общих решений. Увидеть это наглядно позволит координатная прямая. Отметим на ней множество решений каждого неравенства:

На координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Это говорит о том, что неравенства y ≥ 7 и y ≤ −3 не имеют общих решений. Значит не имеет решений система

А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система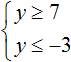

Ответ: решений нет.

Пример 2. Решить систему неравенств

Решим каждое неравенство по отдельности:

Изобразим множество решений неравенств x ≤ −3 и x ≥ 9 на координатной прямой:

Видим, что на координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система

А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система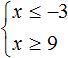

Ответ: решений нет.

Пример 3. Решить систему неравенств

Решим каждое неравенство по отдельности:

Источник

Алгебра. Урок 8. Неравенства, системы неравенств.

Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Неравенства

Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:

то получится неравенство.

Линейные неравенства

Линейные неравенства – это неравенства вида:

a x b a x ≤ b a x > b a x ≥ b

где a и b – любые числа, причем a ≠ 0, x – переменная.

Примеры линейных неравенств:

3 x 5 x − 2 ≥ 0 7 − 5 x 1 x ≤ 0

Решить линейное неравенство – получить выражение вида:

x c x ≤ c x > c x ≥ c

где c – некоторое число.

Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.

Смысл выколотой точки в том, что сама точка в ответ не входит.

Смысл жирной точки в том, что сама точка входит в ответ.

Таблица числовых промежутков

Алгоритм решения линейного неравенства

a x b a x ≤ b a x > b a x ≥ b

Примеры решения линейных неравенств:

№1. Решить неравенство 3 ( 2 − x ) > 18.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )

№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6 x + 4 ≥ 3 x + 3 − 14

6 x − 3 x ≥ 3 − 14 − 4

x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).

Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).

№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

x + 6 − 9 x > − 8 x + 48

Квадратные неравенства

Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.

Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).

Алгоритм решения квадратного неравенства методом интервалов

Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.

Примеры решения квадратных неравенств:

№1. Решить неравенство x 2 ≥ x + 12.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3

x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0

Это значит, что знак на интервале, в котором лежит точка 6 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1

− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1

− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )

№4. Решить неравенство x 2 − 5 x 6.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1

x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0

Это значит, что знак на интервале, в котором лежит точка 10 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

№5. Решить неравенство x 2 4.

Решение:

Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.

( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2

x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0

Это значит, что знак на интервале, в котором лежит точка 3 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

№6. Решить неравенство x 2 + x ≥ 0.

Решение:

Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.

x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1

x 2 + x = 1 2 + 1 = 2 > 0

Это значит, что знак на интервале, в котором лежит точка 1 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )

Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.

Дробно рациональные неравенства

Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).

Примеры дробно рациональных неравенств:

x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3

Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.

Алгоритм решения дробно рациональных неравенств:

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.

Примеры решения дробно рациональных неравенств:

№1. Решить неравенство x − 1 x + 3 > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.

Это значит, что знак на интервале, в котором лежит точка 2 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )

№2. Решить неравенство 3 ( x + 8 ) ≤ 5.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

3 ( x + 8 ) − 5 \ x + 8 ≤ 0

3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 x − 40 x + 8 ≤ 0

x = − 37 5 = − 37 5 = − 7,4

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.

− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )

№3. Решить неравенство x 2 − 1 x > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.

x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )

Системы неравенств

Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.

Пример системы неравенств:

Алгоритм решения системы неравенств

Примеры решений систем неравенств:

№1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Точка 4 на графике жирная, так как знак неравенства нестрогий.

− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный.

Графическая интерпретация решения:

Точка 2 на графике жирная, так как знак неравенства нестрогий.

№2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Точка 3 на графике жирная, так как знак неравенства нестрогий.

Графическая интерпретация решения:

№3. Решить систему неравенств < 3 x + 1 ≤ 2 x x − 7 >5 − x

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Графическая интерпретация решения:

Графическая интерпретация решения:

Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.

№4. Решить систему неравенств < x + 4 >0 2 x + 3 ≤ x 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Графическая интерпретация решения первого неравенства:

Решаем методом интервалов.

D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16

x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1

Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.

Графическая интерпретация решения второго неравенства:

Источник

• ← Что значит решить систему линейных алгебраических уравнений
• Что значит решить систему линейных уравнений →