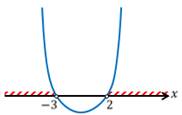
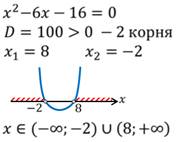
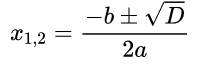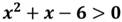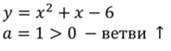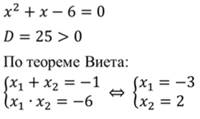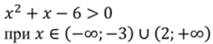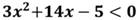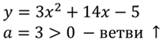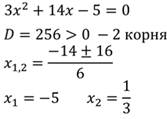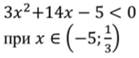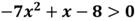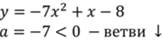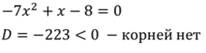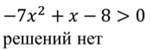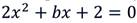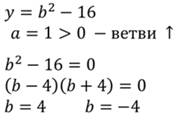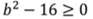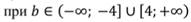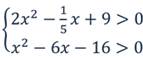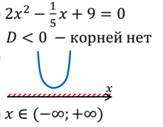Что значит решить неравенство второй степени с одной переменной

Решение неравенств второй степени с одной переменной. Подготовка к ОГЭ. 9-й класс

Разделы: Математика

Класс: 9

Тип урока: урок обобщения и систематизации знаний.

Цели урока:

Ход урока

I. Организационный момент

Приветствие учителя и учащихся. Ознакомление с целями и задачами урока.

II. Актуализация опорных знаний и умений учащихся

1. Фронтальная беседа с классом

— Какая функция называется квадратичной?

— Как называется график квадратичной функции?

— Как определить направление ветвей параболы?

— Как разложить квадратный трехчлен на множители?

— Как найти нули функции?

— От чего зависит количество корней квадратного уравнения?

— Приведите примеры неравенств второй степени.

— Что является решением неравенства?

— Что значит решить неравенство?

2. Устная работа

а) Решите уравнения:

б) Найдите число корней уравнения ax² + bx + c = 0

в) Найдите промежутки, в которых функция y > 0

III. Решение неравенств

Прежде чем перейти к следующему этапу урока, давайте вспомним алгоритм решения неравенств методом интервалов и алгоритм решения неравенств второй степени через график квадратичной функции.

– x² – x + 12 0

1) Рассмотрим функцию y = – x² – x + 12

2) График функции – парабола, ветви направлены вниз (а = –1)

3) Найдем нули функции:

4) Схематически построим график функции и выделим ту часть параболы, для которой y 0.

5) Запишем ответ в виде промежутка

0

1) Рассмотрим функцию y = x² + 2x – 15

2) График функции – парабола, ветви направлены вверх (а = 1)

4) Схематически построим график функции и выделим ту часть параболы, для которой y > 0.

Ответ: (–; –5) U (3; +)

(x + 7)(4 – x) 0

2) Найдем нули функции:

3) Отметим на оси абсцисс нули функции, определим знаки выражения на каждом промежутке, выделим промежутки, в которых функция y 0

3) Отметим на оси абсцисс нули функции, определим знаки выражения на каждом промежутке, выделим промежутки, в которых функция y > 0

Ответ: (–; –1) U (11;+)

(x – 7)² 0

Ответ: (-1;0) U (0;1) U (1;2] U [3;+)

IV. Самостоятельная работа с самопроверкой

V. Итог урока

Сегодня мы вспомнили некоторые способы решения неравенств второй степени. На следующем уроке мы будем решать системы неравенств с одной переменной.

VI. Домашнее задание

Сборник ОГЭ № 8, №21 (варианты 9, 13, 17, 18, 22, 25, 28).

Источник

Квадратные неравенства с одной переменной

теория по математике 📈 неравенства

Неравенство вида ax 2 +bx+c>0 или ax 2 +bx+c

Для решения неравенства находят промежутки, в которых функция у=ax 2 +bx+c принимает положительные или отрицательные значения, это зависит от знака неравенства, данного в стандартном виде. Для этого достаточно определить, в каком направлении расположены ветви параболы у=ax 2 +bx+c, а также найти нули данной функции, относительно которых и определяются промежутки.

Вспомним, что ветви параболы направлены вверх при а>0, ветви направлены вниз при а 2 +bx+c.

Алгоритм решения неравенства второй степени с одной переменной

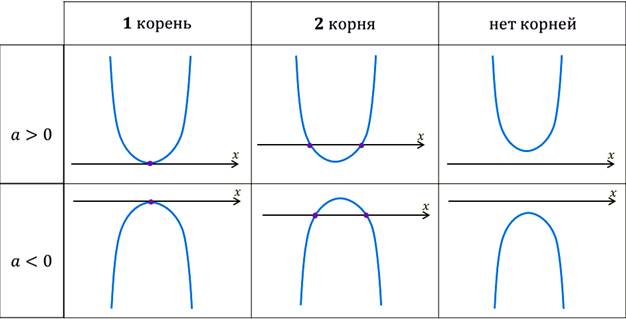
Первый случай. D>0, a>0.

Значит, квадратный трехчлен имеет два корня, находим их по формуле:

Это будут числа –8 и 6. Нам надо на оси х отметить две выколотые точки и построить параболу ветвями вверх, так как число а=1, то есть а>0. Теперь для ответа определяем промежуток отрицательных чисел, так как в условии неравенства стоит знак «меньше».

Это будут все числа, расположенные ниже оси х (на рисунке промежуток заштрихован), в ответ запишем промежуток чисел (–8;6).

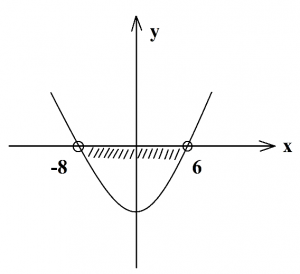
Второй случай. D>0, a 2 +2х+15

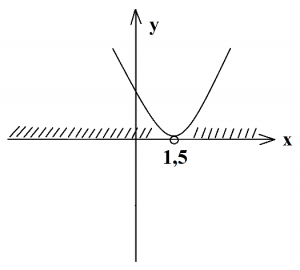
Третий случай. D=0, a 2 –12х+9>0

Находим дискриминант, он равен нулю. Значит, имеем корень, который равен 1,5. Отмечаем на оси х выколотую точку, это будет вершина параболы, проводим параболу ветвями вверх, так как а=4. Теперь определяем промежуток положительных чисел, это все числа, которые находятся выше оси х (показаны штриховкой).

То есть, это числа от минус бесконечности до 1,5 и от 1,5 до плюс бесконечности, так как точка 1,5 выколотая, а значит, она не входит в данный промежуток чисел. Запишем ответ: (-∞;-1,5)∪(1,5:+∞). Также данный ответ можно записать короче: х≠1,5.

Четвертый случай. D 0.

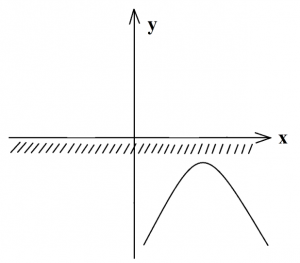
Пятый случай. D 2 +3х–2≤0

Находим дискриминант, он равен отрицательному числу (–71), значит, корней нет. В координатной плоскости покажем параболу, которая не пересекает ось х, то есть, расположена в нижней полуплоскости ветвями вниз, так как а=–10. Теперь для нахождения ответа определяем промежуток отрицательных чисел: так как парабола находится в нижней полуплоскости, а нам нужен промежуток отрицательных чисел (показан штриховкой), то данное неравенство имеет множество решений (искомый промежуток совпал с расположением параболы в нижней полуплоскости).

Записываем ответ: множество решений. Также ответ можно записать в виде промежутка (-∞;+∞) или записать так: х – любое число.

Источник

Алгебра. 9 класс

Неравенства, в одной части которых стоит квадратный трёхчлен, а в другой – нуль, называют неравенствами второй степени с одной переменной.

Для решения неравенств такого вида используют свойства квадратичной функции и её графика. А именно, нули функции и направление ветвей параболы.

Приведём пример. Решим неравенство 3x 2 – 11x – 4 > 0.

Рассмотрим функцию y = 3x 2 – 11x – 4. Графиком этой функции является парабола, ветви которой направлены вверх, так как коэффициент при x 2 равен 4, а 4 > 0.

Для того чтобы выяснить, пересекает ли парабола ось абсцисс и в каких точках, решим квадратное уравнение 3x 2 – 11x – 4 = 0. Это уравнение имеет два корня: и 4.

Покажем схематически, как расположена парабола на координатной плоскости.

На оси абсцисс отметим нули функции, то есть те значения, которые мы получили при решении квадратного уравнения: и 4.

Так как ветви параболы направлены вверх, она будет расположена так.

Обратим внимание, что функция принимает положительные значения, когда или x ∈ (4; +∞), а отрицательные значения, когда .

Таким образом, множеством решений нашего неравенства будет .

Рассмотрим ещё один пример: x 2 – 3x + 4 > 0.

Рассмотрим функцию y = x 2 – 3x + 4. Графиком этой функции является парабола, ветви которой направлены вверх.

Чтобы выяснить, как расположен график данной функции относительно оси абсцисс, решим квадратное уравнение x 2 – 3x + 4 = 0.

Дискриминант этого уравнения меньше нуля, а значит, уравнение не имеет корней.

Значит, парабола не имеет общих точек с осью x. Изобразим схематически расположение параболы на координатной плоскости. Очевидно, что при любом значении переменной x функция принимает положительные значения.

Таким образом, решением рассматриваемого неравенства является любое число.

Источник

Решение неравенств второй степени с одной переменной

Урок 13. Алгебра 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение неравенств второй степени с одной переменной»

В левой части неравенства записан квадратный трёхчлен. Решение неравенства сводится к нахождению множества значений переменной х, при которых квадратный трёхчлен принимает положительные или отрицательные значения.

Алгоритм решения неравенств второй степени:

1. Определить направление ветвей параболы .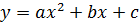

2. Найти корни квадратного уравнения .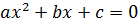

3. Изобразить схематический график.

4. Выбрать множество значений х, соответствующих знаку неравенства.

Решим несколько неравенств второй степени, придерживаясь данного алгоритма.

Рассмотрим квадратичную функцию:

Так как а=1, значит ветви параболы направлены вверх.

Отметим эти значения на оси:

Решением данного неравенства будет объединение промежутков:

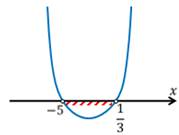
Рассмотрим квадратичную функцию:

Так как а=3, значит ветви параболы направлены вверх.

Решим соответствующее квадратное уравнение:

Отметим эти значения:

Решением данного неравенства будет:

Рассмотрим квадратичную функцию:

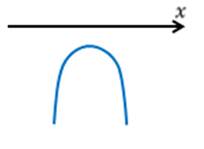
Так как а=-7, значит ветви параболы направлены вниз.

Решим соответствующее квадратное уравнение:

Данное неравенство не имеет решений.

Определить, при каком значении переменной b уравнение имеет корни:

Найдем дискриминант этого уравнения:

Тогда выполнение задания сводиться к решению неравенства второй степени. Причём с нестрогим знаком, больше либо равно.

Применив алгоритм, найдем корни уравнения:

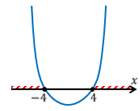
Изобразим их на числовой прямой:

Уравнение имеет корни:

Решить систему неравенств:

Решим каждое неравенство в отдельности.

Мы получили решение двух неравенств второй степени. Вернёмся к системе. Решением системы будет пересечение двух решений. Значит, решением системы будет объединение промежутков:

Источник

Решение неравенств второй степени с одной переменной

МБОУ «Панинская ООШ»

Конспект урока алгебры 9 класс.

Решение неравенств второй степени с одной переменной.

Учитель математики Епишкина Л.В.

Тип урока: Изучение нового материала.

Научить решать неравенства второй степени с одной переменной.

Развивать логическое мышление, математическую речь, познавательный интерес к предмету.

Воспитывать прилежание, трудолюбие, аккуратность, точность.

Изучение нового материала.

Закрепление изученного материала.

Обучающая самостоятельная работа.

1. Актуализация знаний.

– Какую функцию мы изучаем?
– Определение квадратичной функции.
– Давайте поработаем устно, чтобы хорошо усвоить новый материал.

2. Укажите промежутки, в которых функция у=ах 2 +вх+с принимает положительные и отрицательные значения, если её график расположен указанным образом:

– Мы с вами умеем строить график квадратичной функции, умеем решать квадратные уравнения, а сегодня мы должны научиться решать неравенства второй степени с одной переменной.

Запишем тему урока в тетрадь.

3. Изучение нового материала.

Итак, какой формулой задаётся квадратичная функция?

Какой вид имеет квадратное уравнение?

Какой вид имеет квадратный трёхчлен?

Как вы думаете, какой вид будет иметь неравенство второй степени с одной переменной? ах 2 + вх + с > 0 и ах 2 + вх + с

Попробуйте сформулировать определение.

Итак, запишем определение в тетрадь (стр.41).

Решать такие неравенства мы будем с помощью нахождения промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.

Итак, выполним в тетрадях следующее задание:

– Какая квадратичная функция соответствует данному неравенству:

– Что является её графиком?
– Выясним, как расположена парабола относительно оси х.
– Как она может быть расположена (пересекать ось х, находиться выше оси х, ниже оси х , касаться оси х)?
– Как это определить?

2. Нули функции, у = 0.

3. Покажем схематически, как расположена парабола в координатной плоскости.

Запишем алгоритм решения неравенств второй степени с одной переменной.

1. Рассмотреть функцию, соответствующую данному неравенству, определить направление ветвей параболы.
2. Найти нули функции, т.е. абсциссы точек пересечения параболы с осью х, если они есть.
3. Изобразить схематически параболу в координатной плоскости.
4. Выбрать нужные промежутки.
5. Записать ответ.

Рассмотрим пример 3 и пример 4 в учебнике на странице 43. Сделаем соответствующие выводы.

4. Закрепление изученного материала.

Выполняем № 114 (а, в, д).

5. Обучающая самостоятельная работа.

Предлагается решить 3 неравенства, затем на доске показываются правильные ответы, для того, чтобы учащиеся могли проверить свои решения. Во время решения учащиеся консультируются с учителем. Те, кто успешно справится с решением, получат оценки.

Поднятием рук проверяем, как учащиеся усвоили новый материал.

6. Домашнее задание. п.14 №306(а-в)

7. Подведение итогов.

– Какова была цель нашего урока?
– Сформулируйте определение неравенств второй степени с одной переменной.
– Как решать такие неравенства?
– Алгоритм решения.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1272567

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

В Москве новогодние каникулы в школах могут начаться с 27 декабря

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В Хабаровском крае введут уроки по вакцинации в некоторых школах и колледжах

Время чтения: 1 минута

ЕГЭ в 2022 году пройдет в доковидном формате

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник