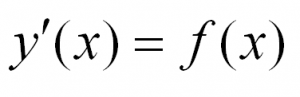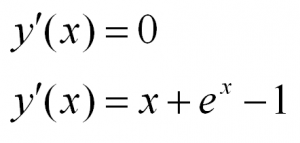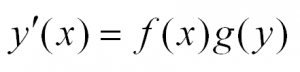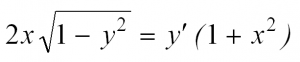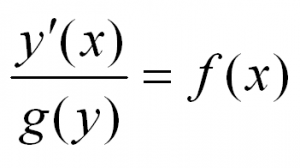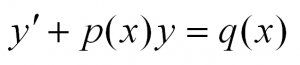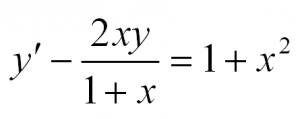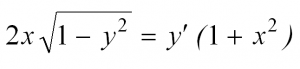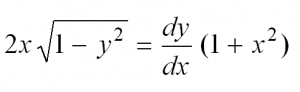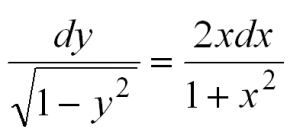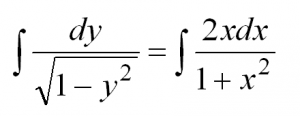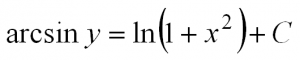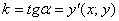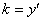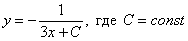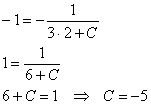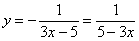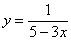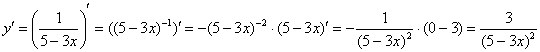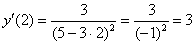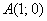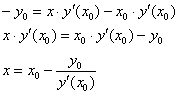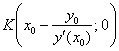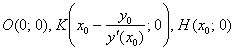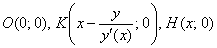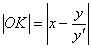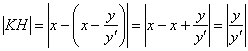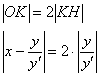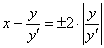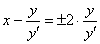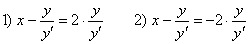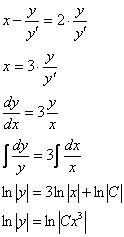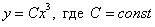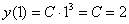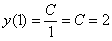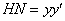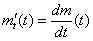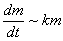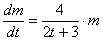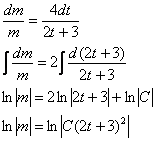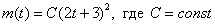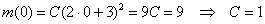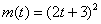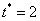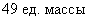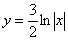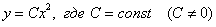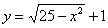Что значит решить дифференциальное уравнение

Дифференциальные уравнения для «чайников». Примеры решения

Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?

Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.

Основные понятия теории дифференциальных уравнений

Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.

Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.

Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.

Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.

Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.

Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.

Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.

Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:

Решить такое уравнение можно, просто проинтегрировав его правую часть.

Примеры таких уравнений:

Уравнения с разделяющимися переменными

В общем виде этот тип уравнений выглядит так:

Решая такое уравнение, нужно разделить переменные, приведя его к виду:

После этого останется проинтегрировать обе части и получить решение.

Линейные дифференциальные уравнения первого порядка

Такие уравнения имеют вид:

Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:

Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).

Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.

Пример решения ДУ с разделяющимися переменными

Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.

Сначала перепишем производную в более привычном виде:

Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:

Теперь осталось проинтегрировать обе части:

Интегрируем и получаем общее решение данного уравнения:

Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Задачи с дифференциальными уравнениями

Ну а как иначе? Если есть дифференциальные уравнения, то должны быть и задачи с ними! Они встречаются в математике (само собой), физике, химии, других науках и, разумеется, соответствующих примеров великое множество – пятилетки не хватит, чтобы все их разобрать. Но этого и не нужно – сегодня наша цель освоить общие принципы решения таких задач, хотя,… штук 50-то всяко осилим)

Начнём с самого главного: вот видим мы текст задачи. Как определить, что её нужно решать с помощью ИМЕННО дифференциального уравнения? Очень просто. Поскольку корнями диффуров являются функции, то по условию так или иначе потребуется найти:

функцию / уравнение / линию / кривую / закон / зависимость и т.д.

В большинстве тематических задач фигурируют дифференциальные уравнения первого порядка, с них и начнём. Как вы прекрасно знаете, в оные уравнения обязательно входит первая производная, и поэтому для освоения урока нужно понимать (очевидно-невероятно), что такое производная. Впрочем, уважаемые студенты, пощады не ждите – я вам обязательно напомню =) И моя беспощадность такова, что мы займёмся этим прямо сейчас:

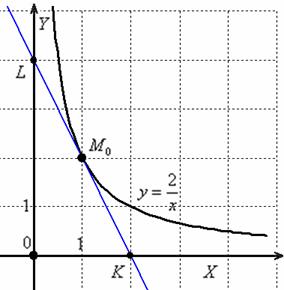
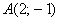
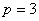
Кривая проходит через точку и обладает тем свойством, что угловой коэффициент касательной в любой её точке пропорционален квадрату ординаты точки касания с коэффициентом пропорциональности . Найти уравнение этой кривой.

Пожалуйста, типичный признак – условие запрашивает у нас уравнение кривой, а значит, задача решается с помощью дифференциального уравнения.

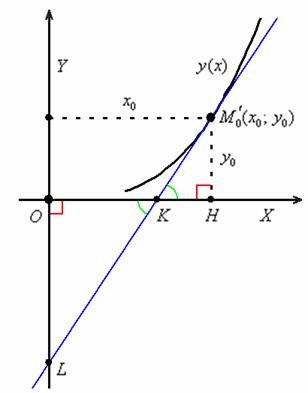
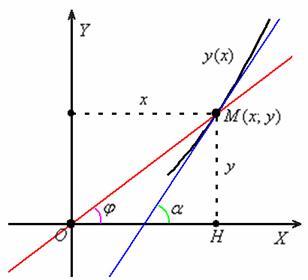
Решение: на первом шаге нужно это самое уравнение составить. Рассмотрим произвольную точку 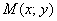, принадлежащую искомой кривой. Заметьте, что этой хитрой фразой мы учитываем ВСЕ точки разыскиваемой линии.

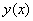
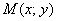
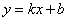
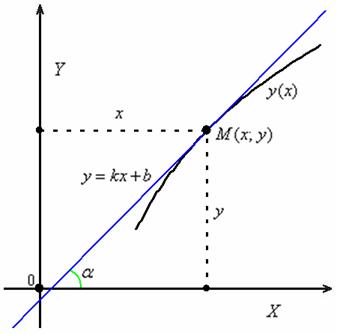
Выполним схематический чертёж, на котором изобразим некоторую кривую , произвольную точку и касательную , проведённую к графику функции в данной точке:

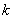
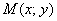
Теперь вспоминаем, что угловой коэффициент касательной равен тангенсу её угла наклона и равен значению производной в точке :

Или, если короче:

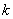
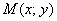
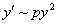
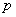
По условию, угловой коэффициент касательной в любой точке кривой пропорционален квадрату ординаты («игрековой» координаты) точки касания:

, где – коэффициент пропорциональности.
(значок «тильда» обозначает пропорциональность)

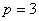
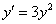
В данной задаче . Таким образом, получаем следующее дифференциальное уравнение:

, которое, понятно, нужно решить 🙂

Перед нами простейшее ДУ с разделяющимися переменными: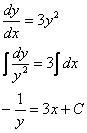

Общее решение:

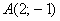
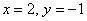
В результате мы получили целое семейство функций, удовлетворяющих критерию задачи. Но в условии есть уточнение: кривая проходит через точку . Решим задачу Коши, т.е. найдём соответствующее частное решение. Здесь удобно непосредственно подставить в общее решение координаты точки:

Таким образом, уравнение, искомой кривой:

Ответ:

Выполним проверку. Она проводится стандартно + желательный анализ, связанный с содержательным смыслом задачи.

Прежде всего, убедимся, что график полученной функции действительно проходит через точку :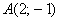

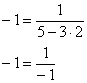
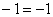
– получено верное равенство, что и требовалось проверить.

Найдём производную:

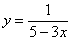
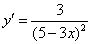
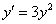
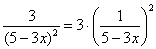
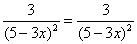
Подставим и в уравнение :

– таким образом, частное решение найдено верно.

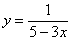
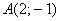
Но это ещё не всё – ведь мы могли неправильно составить само дифференциальное уравнение! И поэтому будет не лишним вернуться условию, согласно которому, любая точка кривой должна обладать следующим свойством: производная функции в точке (угловой коэффициент касательной) равна утроенному квадрату «игрековой» координаты данной точки. Рассмотрим ту же точку и вычислим:

С другой стороны, утроенный квадрат «игрековой» координаты точки :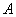
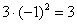
, отлично.

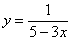
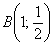
Желающие могут протестировать любую другую точку, принадлежащую кривой , например точку , и убедиться в справедливости только что проверенного критерия. Это, кстати, легко сделать устно.

Вот теперь-то задача «закрыта наглухо». Ну а то, что схематический чертёж далёк от графика гиперболы 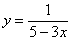– совершенно не страшно, чертёж лишь помогает разобраться в условии. И строить его, к слову, в простых случаях совсем не обязательно 😉 И в самом деле – этого же не требовалось….

Пара типовых задач для самостоятельного решения:

Угловой коэффициент касательной к каждой точке кривой обратно пропорционален абсциссе точки касания с коэффициентом пропорциональности 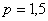. Составить уравнение данной кривой, если известно, что она проходит через точку

Как раз аналогичный пример, в котором вполне можно обойтись без чертежа. Напоминаю, что обратная пропорциональность устроена по принципу «чем больше – тем меньше» – это зависимость… где-то я о ней вроде упоминал…, да, нашёл – в статье о гиперболе. Впрочем, многие помнят этот материал со школы.

И тут ещё хочу предупредить о возможной «накладке» с обозначениями: в «реальных» примерах коэффициент пропорциональности очень часто обозначают буквой 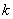, что, конечно, не есть хорошо.

Примерный образец чистового оформления задания в конце урока.

Найти кривую, для которой тангенс угла наклона ее касательной в любой её точке в 2 раза больше тангенса угла наклона прямой, проходящей через ту же точку и начало координат.

А вот здесь уже чертёж не помешает – рассматриваем прямоугольный треугольник, на всякий пожарный: тангенс – это отношение противолежащего катета к прилежащему катету. Впрочем, «картинку» этой задачи опять же несложно «обработать в уме». Но в образце решения я не поленился и выполнил схематический чертёж. И таки догадайтесь, как правильно записать ответ – проанализируйте полученное решение на соответствие условию задачи 😉

Как видите, задачки вроде бы элементарные, а «подводных камней» в них хватает. И перед тем как перейти от «чистой математики» к приложениям (по физике, химии и т.д.) я рассмотрю пару «настоящих» примеров.

Во многих случаях вам придётся столкнуться с задачей из сборника А.П. Рябушко (Часть 2, ИДЗ 11.4, Задача № 4) или из сборника Кузнецова. Или же с какой-то похожей задачей.

Первый источник отличается меньшей сложностью, и что особо приятно, каждая из 30 задач снабжена правильным ответом. Однако здесь нужно помнить, что решение диффура обычно можно записать несколькими способами, и формально результаты могут не совпасть.

Примеры из задачника Л.А. Кузнецова (Раздел V Дифференциальные уравнения, Задача 9) более трудны, но зато по Интернету давным-давно «гуляют» готовые решения всех вариантов. Может быть, найдёте и свою задачу! Однако не спешите радоваться «халяве» и бездумно переписывать материалы – неточностей там хватает.

Гораздо выгоднее ОДИН РАЗ РАЗОБРАТЬСЯ в технике решения таких задач!

Я подробно остановлюсь на заданиях из вариантов 11-20 сборника Кузнецова, которые, как показывает практика, вызывают наибольшие затруднения у студентов, и разберу пример 12-го варианта, который, кстати, в указанном выше источнике вообще решён неправильно:

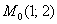
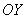
Найти линию, проходящую через точку , если отрезок любой ее касательной между точкой касания и осью делится в точке пересечения с осью абсцисс в отношении (считая от оси ).

Прежде всего, снова обратим внимание на то, что по условию требуется найти линию, следовательно, участь наша – дифференциальное уравнение. И, кроме того, речь идёт о касательной, которая, как вы уже вспомнили, определяется через производную.

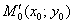
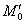
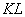
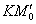
Решение: должен предупредить, что здесь опять возникают «накладки» с обозначениями, и я буду придерживаться собственной версии оформления, которая показалась мне наиболее удобной. Сначала рассмотрим некоторую конкретную точку , принадлежащую искомой линии, и соответствующую касательную. Выполним схематический чертёж. Из условия задачи следует, что точка пересечения касательной с осью лежит строго между точек и . Это принципиальный момент! – так бывает далеко не всегда. И, конечно, нужно постараться, чтобы отрезок был примерно в 2 раза длиннее отрезка :

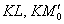
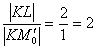
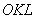
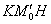
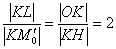
Первое, что приходит в голову – это найти длины отрезков и составить уравнение по формуле . Так решать можно,… но лучше не нужно. Вспоминаем школу: треугольники и подобны по двум углам (обозначены красными и зелёными дугами), а значит, соответствующие стороны этих треугольников пропорциональны:

Грубо говоря, нижний треугольник в 2 раза больше, чем верхний.

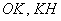
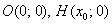
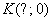
В чём фишка? Фишка состоит в том, что длины отрезков найти значительно проще! Тем более, точки уже известны, и по существу, осталось найти «иксовую» координату точки . Находим:

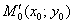
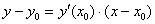
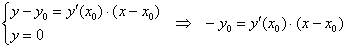
Уравнение касательной к графику функции в точке имеет вид , и чтобы найти, где она пересекает ось абсцисс, нужно решить простейшую систему линейных уравнений:
, откуда выражаем «иксовую» координату точки «ка»:

Таким образом:

Для удобства запишу рабочие точки по порядку:

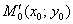
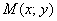
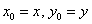
Теперь вернёмся к следующему моменту: изначально мы рассматривали некоторую конкретную точку , и сейчас настал черёд перейти к произвольной точке разыскиваемой линии. Проведём замены :

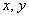
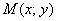
! Примечание: этим приёмом я избежал технической «накладки» с буквами: сначала переменные обозначали, то, что они обычно обозначает, а после замен стали символизировать координаты произвольной точки , принадлежащей искомой кривой.

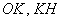
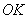
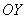
Длины отрезков можно найти по стандартной формуле длины отрезка, но опять – зачем нам нагромождения корней? Длина отрезка , очевидно, равна модулю его «иксовой» координаты (по той причине, что она может быть и отрицательна – отобразите чертёж симметрично относительно оси ):

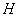
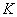
Длину второго отрезка найдём как разность «иксовых» координат точек и , которую из тех же соображений заключим под знак модуля:

В соответствии с обоснованной выше пропорцией 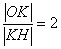, составим дифференциальное уравнение. Удобнее сразу записать так:

Сначала раскроем левый модуль:

При избавлении от правого модуля дробь может получиться как положительной, так и отрицательной, и поэтому всё так и останется:

В результате у нас получилось два дифференциальных уравнения:

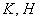
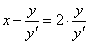
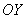
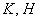
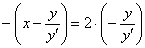
Условию задачи удовлетворяет первое уравнение. Почему? Давайте посмотрим на чертёж: на нём координаты точек положительны, и для этого частного расположения точек мы получаем непосредственно уравнение (проведите рассуждения без модулей). Теперь мысленно отобразите чертёж симметрично относительно оси . Координаты точек станут отрицательными, и в результате «зеркальных» выкладок мы придём к уравнению , т.е. к тому же самому уравнению, которое и соответствует геометрической ситуации нашей задачи (в нижней полуплоскости получаются 2 аналогичных случая).

Вообще, при оформлении практической задачи обо всех этих тонкостях лучше аккуратно умолчать =) и сразу приступить к решению нужного уравнения:

Общее решение:

По условию, линия должна проходить через точку 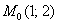. Решим задачу Коши:

Ответ: 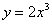– искомая линия.

Как я отмечал выше, задачу можно разрулить и через «очевидное» отношение 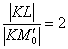, но вычисления получатся просто хардкорными, а результат тот же самый – короткое равенство с двумя модулями.

Желающие могут выполнить чертёж в масштабе 1ед. = 2 тетрадные клетки – изобразить кубическую параболу, удобную касательную и всё измерить линеечкой =) Улыбка улыбкой, но это, кстати, может пригодиться, если вы запутаетесь в модулях и будете сомневаться, какой диффур выбрать. Так или иначе, чертёж довольно прост: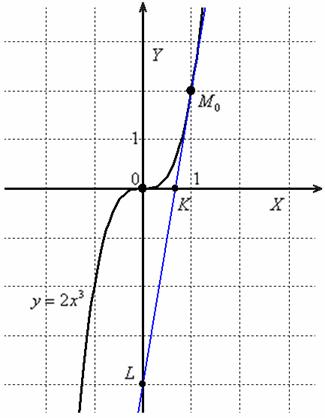

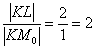
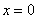
И в самом деле: . Аналогичное соотношение справедливо для любой касательной за исключением касательной в точке (оси абсцисс).

Примечание: здесь не возникает противоречия с условием задачи, в котором предполагается, что касательная пересекает координатные оси в разных точках.

А теперь разберём побочный диффур, который нарисовался в ходе решения: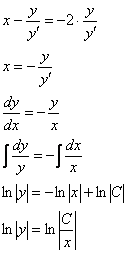

Общее решение: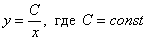
Решим задачу Коши для точки :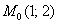

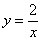
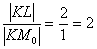
Таким образом, получаем гиперболу . Следует заметить, что здесь тоже выполнено соотношение , нарисую «на скорую руку» одну ветку:

Однако геометрическая ситуация совершенно другая – касательная пересекает координатные оси по разные стороны от точки касания.

Для этого случая условие можно сформулировать несколько по-другому: Найти линию, проходящую через точку 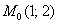, если отрезок любой ее касательной, заключенный между осями координат, делится в точке касания в отношении . И такому расположению касательной посвящены задачи 16-20 сборника Кузнецова.

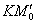
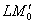
Энтузиасты могут прорешать эту, более простую задачу по трафарету. И, конечно, в ней тоже не надо находить длины отрезков и – намного выгоднее снова рассмотреть подобные треугольники (которые расположены один над другим и так оказалось, что вообще равны). Интересно, что в ходе решения опять появятся два диффура, из которых потребуется выбрать «правильный».

Для самостоятельного решения также предлагаю ещё одно задание:

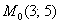
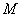
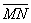
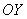
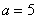
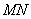
Найти линию, проходящую через точку и обладающую тем свойством, что в любой её точке нормальный вектор с концом на оси имеет длину, равную , и отрезок образует острый угол с положительным направлением оси .

Систематизируем схему решения:

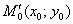
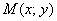
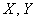
1) Во избежание неразберихи с «иксом» и «игреком» рассматриваем некоторую конкретную точку , принадлежащую искомой прямой. Вообще говоря, можно сразу работать с произвольной точкой , но тогда «глобальные» переменные придётся обозначить как-нибудь по-другому, например, через .

2) Составляем уравнение нормали, проходящей через точку .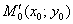

3) Находим координаты точки 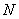пересечения нормали с осью ординат.

4) Находим длину вектора 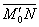. А вот здесь уже без корня обойтись трудно.

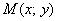
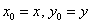
5) Теперь переходим к рассмотрению произвольной точки , т.е. выполняем замены . Этот шаг можно выполнить и чуть раньше (до нахождения длины вектора).

6) Составляем и решаем дифференциальное уравнение. В ходе решения используем информацию о том, что отрезок образует острый угол с положительным направлением оси .

Однако здесь существует и более короткое решение, которым поделилась одна из читательниц сайта. В своё время (когда создавалась статья) из моего поле зрения выпала эта элементарная возможность, и поэтому в конце урока я, конечно же, добавил 2-й способ. Постарайтесь его увидеть! И спасибо за ваши письма – они действительно помогают улучшить учебные материалы.

Я не сторонник различного рода справочников, но для решения практических задач могут пригодиться следующие готовые формулы: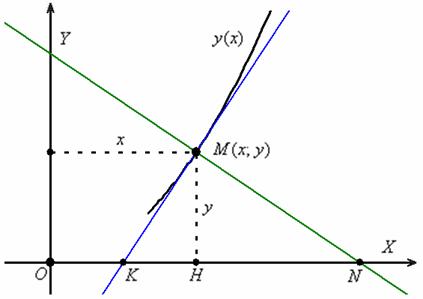

Длина отрезка касательной: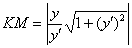
Подкасательная: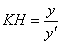
Длина отрезка нормали: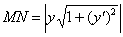
Поднормаль:

Но всё же старайтесь их выводить по ходу решения той или иной задачи.

Поскольку сайт посвящен математике, то бОльшую часть урока заняла математика =), но, разумеется, я не могу обойти стороной многочисленные прикладные задачи, которые рассматриваются даже в школе. Их часто (и может быть даже корректнее) называют задачами, которые ПРИВОДЯТ к понятию дифференциального уравнения. Отличительной особенностью этих задач (как правило) является тот факт, что условие опирается на сам СМЫСЛ производной, то есть речь в нём идёт о скорости изменения некоторого показателя.

Физика, химия,… да чего тут занудничать – биология:

Требуется составить дифференциальное уравнение динамики развития некоторого биологического вида и найти решение этого уравнения.

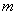
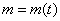
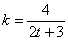
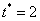
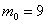
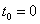
Состояние популяции можно охарактеризовать массой этой популяции (весом всего стада), причем масса является функцией времени . Считая, что скорость роста биомассы пропорциональна биомассе популяции с коэффициентом пропорциональности , найти массу стада в момент времени , если известно её значение при .

…надо сказать, автор задачи не стал мучить студентов-зоотехников и расписал всё подробнейшим образом. Давайте, тем не менее, остановимся на характерных признаках, позволяющих определить, что тут замешано дифференциальное уравнение:

– во-первых, нам явно придётся отыскать функцию 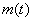массы стада, зависящую от времени;

– и, во-вторых, в условии прямо сказано о скорости роста этой самой массы.

А за скорость роста у нас отвечает производная функция, в данном случае функция

На самом деле решение очень простое и напоминает оно 1-ю задачу урока. По условию, скорость изменения массы стада пропорциональна этой массе:

В большинстве практических задач коэффициент пропорциональности равен константе, но вот здесь он представляет собой функцию: 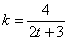. Впрочем, это не имеет особого значения:

Разделяем и властвуем:

Общее решение:

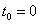
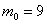
По условию, в момент времени биомасса составляет . Решим задачу Коши:

Таким образом, закон изменения массы популяции:

Шустрая, однако, популяция – прямо какое-то стадо кроликов… или даже саранчи. …Хотя в задаче ничего не сказано о размерности величин. И поэтому, кстати, здесь будет корректно говорить о единицах времени и единицах массы.

Найдём то, что требовалось найти:
– масса стада в момент времени

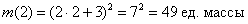
Ответ:

Таблетка массой 0,5 г брошена в стакан воды. Скорость растворения таблетки пропорциональна массе таблетки. Через какое время растворится 99% вещества, если известно, что через 10 минут растворилось 80%?

Это очень простая… и не простая задача 😉 Постарайтесь самым тщательным образом разобраться в решении, задач в подобном техническом исполнении намного больше стакана – их пруд пруди. И кто позабыл – свойства степеней и логарифмов в помощь.

К сожалению, нельзя объять необъятное, и около 10 готовых задач по физике я загрузил в библиотеку, в основном, там задачи по механике. Физика не является моим профильным предметом, но вроде получилось неплохо….

Что касается дифуров 2-го и более высоких порядков, то на практике они встречаются намного реже. Здесь можно отметить задачи на 2-й закон Ньютона (простейшее ДУ, допускающее понижение порядка – см. по ссылке выше), а также задачу о свободных и вынужденных колебаниях (линейные ОДУ и НДУ 2-го порядка). Теоретический материал по последней задаче можно посмотреть здесь.

Спасибо за внимание – надеюсь, урок был полезен, и теперь вы сможете справиться с любой тематической задачей!

Задача 2: Решение: рассмотрим произвольную точку , принадлежащую искомой кривой. По условию, угловой коэффициент касательной к кривой в данной точке:

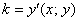
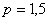
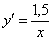
Учитывая, что и , получаем следующее дифференциальное уравнение:

Разделяем переменные и интегрируем:

Общее решение: .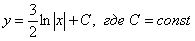
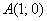
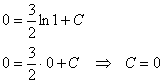
Найдём кривую, которая проходит через точку . Решим задачу Коши:

Ответ:

Задача 3: Решение: рассмотрим произвольную точку 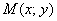, принадлежащую искомой кривой, и соответствующую касательную:

Согласно геометрическому смыслу производной: .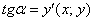
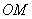
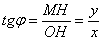
Проведём прямую и рассмотрим прямоугольный треугольник . По определению тангенса:

По условию задачи: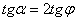

Таким образом, получаем следующее дифференциальное уравнение: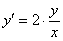

Разделяем переменные и интегрируем: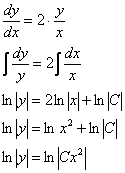

Общее решение: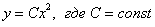
Поскольку уравнение 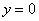(ось абсцисс) не удовлетворяет условию задачи, то значение следует исключить из множества решений.
Ответ: семейство парабол:

Задача 5: Решение: рассмотрим некоторую точку , принадлежащую искомой линии. Выполним схематический чертёж:

Составим уравнение нормали, проходящей через точку :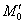

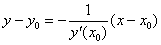
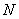
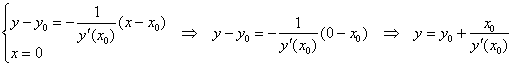
Найдём точку пересечения нормали с осью ординат:

Таким образом: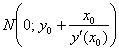
Вычислим длину вектора: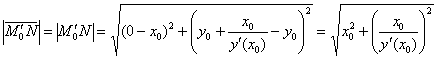

Рассмотрим произвольную точку , принадлежащую искомой кривой:


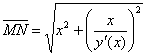
По условию: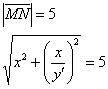

Возведём обе части в квадрат и выполним дальнейшие преобразования:

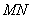
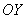
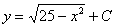
Так как отрезок образует острый угол с положительным направлением оси , то выбираем верхнюю полуокружность:

Решим задачу Коши для точки :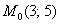

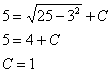
Ответ:

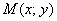
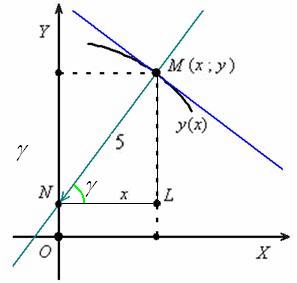
Второй способ решения: пусть точка , принадлежит искомой кривой:

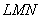
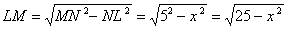
Рассмотрим прямоугольный треугольник . По теореме Пифагора:

Таким образом, тангенс угла наклона нормали: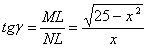

У перпендикулярных прямых угловые коэффициенты взаимнообратны и противоположны по знаку (см. статью Задачи с прямой), поэтому тангенс угла наклона касательной: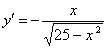

Разделяем переменные и интегрируем:

Решим задачу Коши для точки :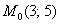

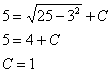
Ответ:

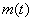
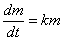
Задача 7: Решение: рассмотрим функцию изменения массы таблетки. В соответствии с условием:
(коэффициент пропорциональности пока не известен)
Разделяем переменные и интегрируем:

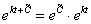
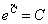
Примечание: здесь выполнено преобразование с последующим переобозначением константы: .
В начальный момент времени масса таблетки составляла 0,5 г. Решим задачу Коши: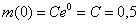

В результате: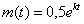
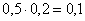
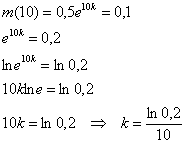
Известно, что через 10 минут растворилось 80% таблетки, т.е. осталось г твёрдого вещества. Найдём значение параметра:

Таким образом: 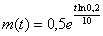– закон изменения массы (растворения) таблетки.
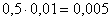
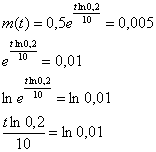
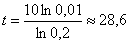
Найдём, через какое время растворится 99% таблетки. Поскольку твёрдого вещества останется г, то:

мин.
Ответ: примерно через 28,6 мин

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Источник