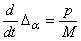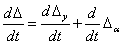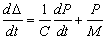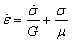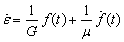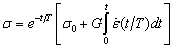Что значит реологические свойства
Реологические свойства
Литература : Гальперин A. M., Шафаренко E. M., Pеологические расчеты горнотехнических сооружений, M., 1977; Tурчанинов И. A., Иофис M. A., Kаспарьян Э. B., Oсновы механики горных пород, Л., 1977.
Ю. И. Бурчаков.
Полезное
Смотреть что такое «Реологические свойства» в других словарях:
реологические свойства — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN flow properties … Справочник технического переводчика
реологические свойства горной породы — Механические свойства, отражающие влияние длительного воздействия нагрузок на изменение напряженно деформированного состояния горных пород. [ГОСТ Р 50544 93] Тематики горные породы Обобщающие термины физические свойства горных пород EN flowing… … Справочник технического переводчика
реологические свойства (буровых растворов) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN flow characteristics … Справочник технического переводчика
реологические свойства буровых растворов — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN flow characteristics of muds … Справочник технического переводчика
реологические свойства макаронного теста — Соотношение упругих, пластичных и прочностных свойств макаронного теста в заданных условиях. [ГОСТ Р 52000 2002] Тематики макаронные изделия … Справочник технического переводчика
реологические свойства горной породы — 3.19 реологические свойства горной породы : Механические свойства, отражающие влияние длительного воздействия нагрузок на изменение напряженно деформированного состояния горных пород. Источник: СП 123.13330.2012: Подземные хранилища газа, нефти и … Словарь-справочник терминов нормативно-технической документации
реагент для снижения водоотдачи буровых растворов, улучшающий их реологические свойства — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN Qualex (sodium carboxymethyl cellulose) … Справочник технического переводчика
Механические свойства — горных пород (a. mechanical properties of rocks; н. mechanische Eigenschaften der Gesteine; ф. proprietes mecaniques des roches; и. caracteristicas mecanicas de rocas, propiedades mecanicas de rocas) характеризуют изменения формы,… … Геологическая энциклопедия
ГОСТ 30330-95: Породы горные. Термины и определения — Терминология ГОСТ 30330 95: Породы горные. Термины и определения оригинал документа: 161 абразивность горной породы Горно технологическое свойство, характеризующее способность горной породы изнашивать контактирующие с ней поверхности Определения… … Словарь-справочник терминов нормативно-технической документации
ГОСТ Р 50544-93: Породы горные. Термины и определения — Терминология ГОСТ Р 50544 93: Породы горные. Термины и определения оригинал документа: 161 абразивность горной породы Горно технологическое свойство, характеризующее способность горной породы изнашивать контактирующие с ней поверхности… … Словарь-справочник терминов нормативно-технической документации
Реологические свойства
Реология — это учение о текучести материалов. Текучесть жидкости измеряется вязкостью, текучесть твердых веществ — ползучестью (крипом) и вязкоэластичностью.
Вязкость
Когда вещество течет под воздействием прилагаемой к нему нагрузки (например, сил гравитации), молекулы или атомы начинают контактировать с соседними атомами или молекулами. Таким образом, имеющиеся связи могут распадаться и образовываться снова, оказывая сопротивление течению. Это сопротивление течению и называется вязкостью.
Для таких жидкостей, как вода, силы связи между молекулами очень малы и легко преодолеваются, поэтому вода легко течет под воздействием сил, прилагаемых извне, и вязкость ее невысока. У некоторых других жидкостей силы межмолекулярного взаимодействия будут намного выше. Обычно такие силы ассоциируются с крупными молекулами, например, молекулами такого известного вещества, как патока. Молекулы в подобных веществах могут переплетаться друг с другом, что делает жидкость очень вязкой.
Рис. 1.8.1. Сдвиг слоя жидкости толщиной d, расположенного между двумя твердыми пластинами. Для движения верхней подвижной пластины относительно неподвижной нижней со скоростью V необходимо приложить силу F для преодоления сопротивления данного слоя жидкости
Эти явления наблюдаются у полимеров с высокой молекулярной массой.
Когда мы перемешиваем жидкость, мы прикладываем усилия, которые создают в жидкости напряжения сдвига, чем энергичнее перемешивается жидкость, тем выше скорость сдвига. Эта ситуация графически показана на Рис. 1.8.1. Напряжение и скорость сдвига определяются соотношениями:
Напряжение сдвига = r\s = F/A
Скорость сдвига = е = V/d
Существует ряд методов измерения напряжения сдвига путем оценки ряда скоростей сдвига для данной жидкости. По значениям скоростей сдвига, полученным экспериментальным путем, строят график в координатах напряжение сдвига — скорость сдвига. Зависимость между напряжением и скоростью сдвига для многих жидкостей является линейной. На Рис. 1.8.2 представлена типичная кривая для такой жидкости. Угол наклона кривой равен вязкости, т), определяемой по формуле: Т| = напряжение сдвига/скорость сдвига. Единицами измерения вязкости являются Паскаль секунды (Пах).
Вещества, для которых соотношение между напряжением и скоростью при сдвиге носит линейный характер, имеют один показатель вязкости для всего диапазона скоростей сдвига, и проявляют «ньютоновские » свойства текучести. Однако линейное соотношение наблюдается далеко не у всех материалов, некоторые имеют другие отличные характеристики, представленные на Рис. 1.8.3.
Рис. 1.8.2. Зависимость напряжения сдвига от скорости для ньютоновской жидкости
Рис. 1.8.3. Графическое представление реологических свойств ряда жидкостей
Жидкости с пластической характеристикой не будут течь, пока приложенное начальное напряжение сдвига не достигнет определенной величины. После этого течение жидкости будет соответствовать ньютоновскому поведению.
У дилатантных (расширяющихся) жидкостей при повышении скорости сдвига будет увеличиваться вязкость. Это означает, что чем быстрее мы будем перемешивать жидкость, тем труднее будет проводить этот процесс. Текучесть таких жидкостей невозможно характеризовать одним единственным показателем вязкости.
Для некоторых жидкостей увеличение скорости сдвига не приводит к соответствующему повышению напряжения сдвига. Это означает, что увеличение скорости сдвига облегчает перемешивание таких веществ, что отличает их от «ньютоновских» или дилантатных жидкостей. Подобное поведение жидкости называют псевдопластическим, оно приводит к распространенному явлению, называемому «разжижением вещества». Примером псевдопластического вещества стоматологического назначения является силиконовый оттискной материал, который за счет разжижения при увеличении скорости сдвига будет значительно легче вытекать из шприца, чем вещество, не обладающее псевдопластичностью.
Тиксотропия
До настоящего момента полагали, что если известны значения напряжения и скорости сдвига в данный момент времени, то можно определить вязкость. Для некоторых веществ при определенной скорости сдвига вязкость будет меняться, и если построить график в системе координат «напряжение сдвига — скорость сдвига», то можно увидеть картину, представленную на Рис. 1.8.4.
Рис. 1.8.4. Характеристика тиксотропного поведения жидкостей
В этом случае, вязкость, наблюдаемая при повы шении скорости сдвига, отличается от таковой, при снижении этой скорости. Подобное явление называется гистерезисом. В таких случаях вязкость жидкости зависит от предшествующих деформаций, которым эта жидкость ранее подвергалась.
Этот тип поведения жидкости наблюдается в тех случаях, когда в результате перемешивания в ней произошло перераспределение молекул, и при этом молекулам не хватило времени снова вернуться к своему нормальному положению, имевшему место до перемешивания. Таким образом, чем дольше перемешивать жидкость с заданной скоростью сдвига, тем ниже будет напряжение сдвига, тем меньше будет вязкость этой жидкости. Однако если жидкость после перемешивания оставить на какое-то время, молекулы вернутся к своему нормальному распределению, и тогда весь процесс можно будет проводить снова. Такой тип поведения жидкости называется тиксотропным. Примером тиксотропной жидкости являются красители, не стекающие с кисти художника.
Клиническое значение
Реологические свойства материалов имеют большое значение потому, что они существенным образом определяют технологические характеристики материала.
Вязкоэластичность
Многие материалы по физическим свойствам находятся где-то посередине между вязкой жидкостью и упругим твердым телом. Считается, что у упругого твердого материала соотношение между напряжением и деформацией не зависит от каких бы то ни было динамических факторов, таких, как скорость приложения нагрузки или скорость деформации. Однако если материал нагружен в течение достаточного времени, в некоторых твердых веществах под воздействием нагрузок происходит перераспределение молекул, что приводит к изменению величины деформации материала. После снятия нагрузки, материал не способен сразу же вернуться в исходное состояние. Это означает, что поведение материала зависит от таких факторов, как «длительность нагрузки» и «величина прилагаемой нагрузки».
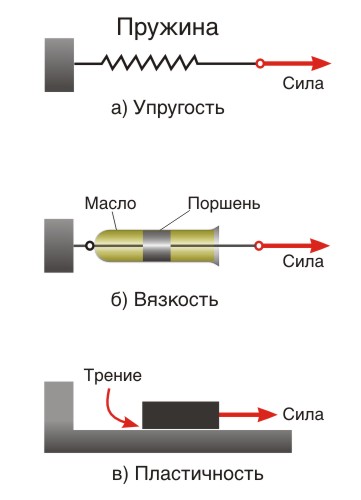
Простым и эффективным способом наглядного представления этих свойств является использование модели, основанной на комбинации пружины и масляного амортизатора, представляющей собой устройство для поглощения энергии удара. Пружина играет роль упругого элемента, а масляный амортизатор — вязкого. Изменение деформации этой модели со временем представлено на Рис.1.8.5. Для пружины приложение нагрузки приведет к моментальной деформации, которая будет сохраняться в течение всего времени действия нагрузки. Сразу же после снятия нагрузки пружина вернется в исходное состояние за счет сил упругости. Для масляного амортизатора, напротив, приложение нагрузки приведет к постепенному нарастанию деформации в течение всего времени
действия нагрузки. После снятия нагрузки деформация не исчезнет, и масляный амортизатор останется в новом положении.
Рис. 1.8.5. Графическая характеристика упругого поведения пружины и вязкого масляного амортизатора
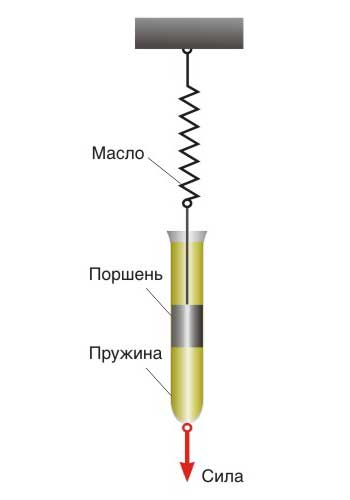
При параллельном соединении этих двух элементов можно получить простую модель вязкоэластичности. Реакция такой модели на нагрузку представлена на Рис. 1.8.6. В этой модели масляный амортизатор препятствует резкой деформации упругой пружины. При этом деформация масляного амортизатора постепенно позволяет пружине приближаться к желаемому состоянию деформирования. При снятии нагрузки, масляный амортизатор препятствует возвращению пружины в исходное состояние, которое, в конце концов, может быть достигнуто через определенное время.
Рис. 1.8.6. Вязкоэластичное поведение пружины и амортизатора, соединенных параллельно
Вязкоэластичными свойствами обладает группа эластомерных оттискных материалов. Кривая в координатах «деформация-время» для эластомеров и отвечающая ей модель, основанная на упругом, вязком и вязкоэластичном элементах, представлена на Рис. 1.8.7. Для того, чтобы избежать избыточной постоянной деформации этих материалов, их не следует нагружать дольше положенного времени. По этой причине эластомерный оттискной материал удаляют из полости рта коротким резким рывком. Чем быстрее будет приложена и снята нагрузка, тем более упругой будет реакция материала.
Рис. 1.8.7. Вязкоэластичная модель реологического поведения полностью отвержденного эластомерного оттискного материала.
Нагрузка, приложенная в момент to приводит к мгновенному растяжению пружины А, а деформация пружины D запаздывает из-за противодействия амортизатора С. Через некоторое время амортизаторы С и В срабатывают и приводят к дальнейшей деформации. В момент t1 нагрузка снимается, пружина А мгновенно возвращается в исходное состояние. Амортизатор С препятствует возвращению пружины D в исходное состояние. Постепенно к моменту t2 пружина возвращается к своей первоначальной длине. Некоторая величина остаточной деформации сохраняется, так как поршень масляного амортизатора В не вернулся в свое исходное положение
Клиническое значение
Некоторые материалы по своим свойствам занимают промежуточное положение между жидкостью и твердым телом, что обуславливает их склонность к деформации.
Основы стоматологического материаловедения
Ричард ван Нурт
РЕОЛОГИЯ
РЕОЛОГИЯ – наука о деформациях и текучести сплошных сред, обнаруживающих упругие, пластические и вязкие свойства в различных сочетаниях. Упругие деформации возникают в теле при приложении нагрузки и исчезают, если нагрузки снять; пластические деформации появляются только в том случае, когда вызванные нагрузкой напряжения превышают известную величину – предел текучести; они сохраняются после снятия нагрузки; вязкое течение отличается тем, что оно возникает при любых сколь угодно малых напряжениях, с ростом напряжений увеличивается скорость течения, и при сохранении напряжений вязкое течение продолжается неограниченно. Еще одно свойство, которым могут обладать среды, изучаемые реологией, – это высокоэластичность, характерная, например, для резины, когда резиновая лента допускает десятикратное растяжение, а после снятия нагрузки практически мгновенно восстанавливает первоначальное состояние.
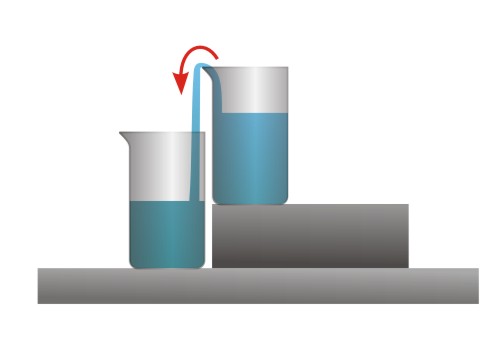
Типичный реологический процесс – это сравнительно медленное течение вещества, в котором обнаруживаются упругие, пластические или высокоэластические свойства. Само слово реология происходит от греческого rew – течение; афоризм «все течет» по-гречески звучит panta rei – (па’нта ре’и). Реологические явления проявляются во многих природных процессах и в большом числе технологических. Очень многочисленны вещества, участвующие в таких процессах: это породы, составляющие земную кору, магма, вулканическая лава, это нефть и глинистые растворы, играющие важнейшую роль в добыче нефти; влажная глина, цементная паста, бетон и асфальтобетон (смесь асфальта и песка, которой покрывают тротуар), это масляные краски – смесь масла и частиц пигмента; это растворы и расплавы полимеров в процессе изготовления нитей, пленок, труб путем экструзии; наконец, это – хлебное тесто и тестообразные массы, из которых изготовляют конфеты, сосиски, кремы, мази, зубные пасты, это твердое топливо для ракет; это, наконец, белковые тела, например, мышечные ткани. В этот не полный перечень «реологических» сред входят как тела, которые естественно считать твердыми (бетон), так и жидкие – нефть. Еще один опыт можно провести с высокомолекулярным раствором полиэтиленоксида в воде. Если, наклонив стакан А, начать переливать из него раствор в нижний стакан Б (рис. 1), а потом аккуратно вернуть стакан А на место, то окажется, что тонкая струйка раствора продолжает перетекать из верхнего стакана в нижний: интересно, что эта струйка сначала поднимается вверх по вертикальной стенке стакана А, а затем, переливается через край и стекает вниз, в стакан Б – это своеобразный сифон, но без сифонной трубки.
Совсем простой опыт невольно ставит тот, кто испачкал пальцы смолой, резиновым клеем или густым сахарным сиропом: попытка разлепить пальцы приводит к образованию упругих нитей, которые вытягиваются из текучей среды. Именно так образуется паутина и шелковая нить.
Итак, механические свойства разных реологических сред, во-первых, весьма разнообразны, и, во-вторых, оказываются существенно различными в зависимости от условий нагружения.
Очень многие реологические среды являются дисперсными системами двух или трех фаз: это мелкие твердые частицы, распределенные в вязкой жидкости (суспензия или гель, если твердая фаза преобладает), или это мелкие капельки одной жидкости в другой – эмульсия, или пузырьки воздуха в жидкости (пена), и т.д. Но, тем не менее, реология рассматривает такую среду как однородную, но обнаруживающую такие же механические свойства, как и те, что установлены в опытах с реальным конкретным материалом. Этот подход, характерный для механики сплошных сред, позволяет избежать трудностей, связанных с изучением механизмов взаимодействия фаз, и сравнительно просто описать основные черты поведения реологических сред при воздействии на них заданных нагрузок. Такие теории называются феноменологическими.
Математическая модель механических свойств данной среды задается уравнением, связывающим напряжения, имеющиеся в окрестности некоторой точки среды, и деформации, возникающие вследствие этого, причем в это уравнение могут входить и скорости напряжений и деформаций, т.е. их производные по времени, и интегралы по времени от напряжений или деформаций.
Это уравнение называется реологическим уравнением состояния среды или ее определяющим соотношением, и играет роль, аналогичную роли уравнения состояния идеального газа, нужно только иметь в виду, что уравнение состояния газа гораздо точнее отражает свойства конкретного газа, чем реологическое уравнение – свойства некоторой вязко-упруго-текучей среды, что объясняется очевидной причиной – очень высокой сложностью тех сред, которые изучает реология.
Определяющее соотношение должно быть сформулировано как связь тензоров напряжений и деформаций на основе всех известных опытных данных, но сами опыты эту связь не устанавливают, а лишь показывают ее проявления в некоторых частных случаях.
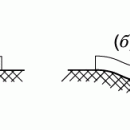
Простой и наглядный способ построения реологического уравнения состояния состоит в том, что каждое основное свойство среды можно смоделировать подходящим элементом, то есть упругость – пружинкой, вязкость – поршнем в цилиндре с вязкой жидкостью, пластичность – элементом с сухим трением (рис. 2).
Соединив тем или иным образом эти элементы, получают модель образца для механических испытаний, свойства которого в общих чертах можно определить теоретически. Это позволяет, изучив опыты с конкретным материалом, подобрать такое соединение элементов, чтобы обеспечить качественное соответствие реальным опытам, подбирая жесткость пружинки, вязкость масла в поршне, величину коэффициента сухого трения, можно добиться достаточно точного совпадения экспериментальных кривых и их модельного представления (если, конечно, структура модели правильно организована и достаточно богата для описания данного материала). Если модель из элементов построена, то написание математического соотношения производится по определенным правилам, причем сравнительно простым.
Модель, составленную из пружинок и поршеньков, можно только растягивать, но растяжению в модели могут соответствовать и сжатие, и сдвиг, и объемная деформация в натурной среде.
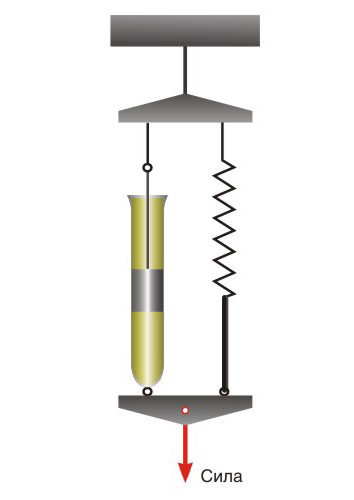
Можно построить модель вязко-упругого тела, последовательно соединив упругий и вязкий элементы (рис. 3).
Если эту систему быстро нагрузить (дернуть), то вязкий элемент не успеет сдвинуться с места и будет вести себя, как замороженный, а деформацию возьмет на себя пружина – и модель ведет себя как упругое тело. Наоборот, при медленном нагружении, например, при постоянной силе, к некоторой небольшой постоянной деформации пружины прибавляется в принципе неограниченно возрастающая деформация вязкого элемента, т.е. модель ведет себя как упругая жидкость, которую называют жидкостью Максвелла (а также телом или моделью Максвелла). Эта жидкость не подчиняется закону вязкости Ньютона и поэтому называется неньютоновской жидкостью.
Закон Гука применительно к пружине имеет вид
где Dg – упругое удлинение пружины, P – сила, C – жесткость пружины.
Для вязкой жидкости справедлив закон Ньютона, который применительно к перемещению поршня в цилиндре дает
здесь Da – вязкое смещение поршня в цилиндре, M – коэффициент вязкого сопротивления.
Уравнение, описывающее зависимость удлинения модели (рис. 3) D от величины силы 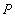
Таким образом, уравнение модели имеет вид:
и за время T уменьшается в e раз, (e » 2,71828 – основание натуральных логарифмов). Таким образом, время релаксации T характеризует скорость убывания напряжений в описанном процессе при e = const, который называется процессом релаксации.
Реологическое уравнение Максвелла пригодно для качественного описания процессов в стекловидных и полимерных материалах. Для хорошего количественного описания используются более сложные модели.
Выражение для s = f(t) содержит интеграл по времени от начала процесса до текущего момента; поэтому значение напряжения s в момент t зависит от значений e во все предшествующие моменты от 0 до t, поэтому такие модели называют «материалами с памятью».
Для описания реологических свойств суглинка, имеющего структуру геля, в котором частицы песка соединяются цепочками коллоидных частиц глины, а промежутки заполнены водой, Кельвин предложил схему, в которой упругий и вязкий элементы соединены параллельно, т.е. так, что их деформации одинаковы (рис. 4).
Соответствующее реологическое уравнение получается аналогично тому, как это сделано для среды Максвелла, но с учетом того, что в модели Кельвина одинаковы деформации элементов, а общее напряжение получается суммированием напряжений в вязком и упругом элементах:
Анализ показывает, что среда Кельвина является твердым телом, похожим на губку, пропитанную вязкой жидкостью.
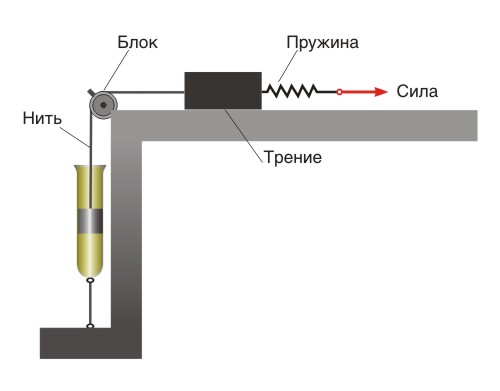
Примером более сложной модели является среда Бингама, модель которой представлена на рис. 4. Если увеличивать силу P, то сначала деформируется только пружина; затем, при определенном значении силы P, преодолевается сила трения бруска о поверхность и начинается его движение, сопротивление которому оказывает не только трение, но и вязкое сопротивление поршня в цилиндре (рис. 5).
Считается, что реология началась именно с этой модели, не укладывающейся в рамки взаимодействия классических сред – упругого тела и вязкой жидкости. Среда Бингама была введена для описания поведения свежей масляной краски, когда было установлено, что она является пластическим твердым телом, а не вязкой жидкостью.
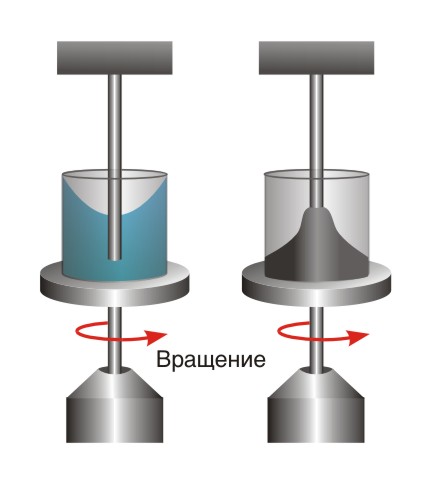
Реологические модели, получаемые путем комбинирования основных элементов (упругость, вязкость, трение) качественно описывают поведение под нагрузкой реальных сред, но наблюдаются при этом значительные количественные отклонения. Но известны эффекты, для описания которых в настоящее время еще не создана удовлетворительная теория. В первую очередь, это так называемый эффект Вайсенберга. Он проявляется, в частности, в следующем опыте (рис. 6): Пусть есть два одинаковых стакана – один с ньютоновской вязкой жидкостью, например, с растительным маслом, другой – с концентрированным раствором высокополимерного вещества (например, сладкого сгущенного молока); оба стакана приводятся во вращение вокруг своих осей. Сверху в стаканы опущены неподвижные круглые стержни. В стакане с маслом видна ожидаемая картина – жидкость принимает форму тела вращения с параболической поверхностью, вертикальная координата которой возрастает с удалением от центра. Но в другом стакане жидкость начнет медленно подниматься по центральному неподвижному стержню, в результате чего уровень поверхности у оси оказывается выше, чем у краев.
Не менее интересен и «эффект Томса». В 1940-х многие исследователи замечали, что течение жидкости по трубопроводу сильно облегчается (снижается гидравлическое сопротивление), если в низкомолекулярную жидкость добавить очень малое (доли процента) количество растворимого полимера. Оказалось, что можно достигнуть четырехкратного снижения гидравлического сопротивления воды в трубе, добавляя несколько миллионных долей (по весу) подходящего высокомолекулярного вещества. Этот эффект используется в некоторых нефтепроводах, пожарных шлангах; есть исследования по снижению кровяного давления у животных.
Изучение реальных сред со сложными свойствами не обязательно относят к реологии: теория неньютоновской жидкостей, теория вязкоупругости и вязкопластичности, теория ползучести металлов при высоких температурах, механика природных процессов – это самостоятельные научные направления, с которыми связаны многие важнейшие достижения как в области теории, так и в области практики – от медицины до космоса, от снежных лавин до дрейфа континентов.
Рейнер М. Деформация и течение. М., 1963
Рейнер М. Реология. М., Наука, 1965
Бленд Д. Теория линейной вязкоупругости. М., 1965
Работнов Ю.Н. Теория ползучести. М., Наука, 1966
Лодж А.С. Эластичные жидкости. М., 1969
Шульман З.П. Беседы о реофизике. Минск, Наука и техника, 1976