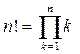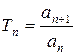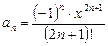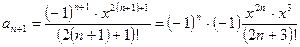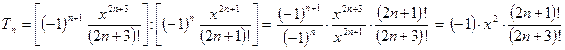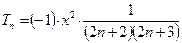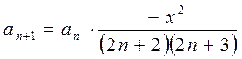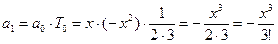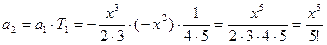Что значит рекуррентная формула
Рекуррентная формула
При суммировании ряда необходимо решить следующие задачи:
a) свести вычисления к простейшим арифметическим операциям;
b) уменьшить число этих операций и время расчета;
c) уменьшить погрешность округления.
Рассмотрим вычисление функции sin x. Разложение этой функции в ряд Тейлора имеет следующий вид
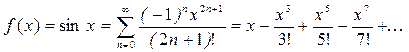
Область сходимости ряда определяется неравенством 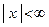
Величина n! называется “n—факториал” и вычисляется по формуле:
n! = 1 × 2 × 3 × … × (n – 1) × n = (n – 1)! × n или
Принято считать, что 0! = 1.
Суммирование ряда последовательным вычислением слагаемых и добавлением их к сумме, как на приведенной выше блок-схеме, сводит вычисления к простейшим арифметическим операциям, то есть первая задача при этом решается. Что касается второй задачи – уменьшения количества этих операций, – то многократное перемножение чисел в числителе (степени x) и в знаменателе (n!) вряд ли можно считать рациональным. При этом (третья задача) погрешность вычислений возрастает с увеличением номера члена ряда – слишком велики становятся и числитель, и знаменатель.
Задачи сокращения количества операций и уменьшения погрешности вычислений решает рекуррентная формула, позволяющая вычислить значение очередного члена ряда, используя уже найденное значение предыдущего. Рекуррентная формула имеет вид:
В нашем примере произвольный член ряда определяется формулой:
Номер начального члена ряда n = 0, его значение a0 = x.
Для расчета коэффициента рекурсии
определим значение следующего (n+1)-го члена ряда.
В формулу общего члена ряда
вместо n подставим (n+1), получим
Вычисляя коэффициент рекурсии, сокращаем дробь:
Чтобы сократить факториалы, рассмотрим числитель и знаменатель отдельно:
(2n + 1)! = 1 × 2 × 3 × … × (2n + 1)
(2n + 3)! = 1 × 2 × 3 × … × (2n + 1) × (2n + 2) × (2n + 3)
Окончательная формула коэффициента рекурсии
Отсюда получаем рекуррентную формулу для вычисления членов ряда
Проверка полученной формулы убережет Вас от ошибок в алгоритме и, возможно, сэкономит усилия при отладке программы.
Подставив n = 0 в формулу общего члена ряда 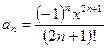
Далее определим по рекуррентной формуле a1 и a2, сверяя результаты с соответствующими членами ряда:
при n = 0
при n = 1
Совпадение полученных значений с членами ряда показывает, что коэффициент рекурсии рассчитан правильно.
Дата добавления: 2017-09-19 ; просмотров: 1223 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Рекуррентная формула
Рекуррентная формула — формула вида 

Общая проблематика вычислений с использованием рекуррентных формул является предметом теории рекурсивных функций.
Содержание
Примеры
Приложения
Рекуррентные формулы используются для описания времени работы алгоритма, рекурсивно обращающегося к самому себе. В такой формуле время, требуемое для решения задачи объемом ввода n, выражается через время решения вспомогательных подзадач. [1]
См. также
Примечания
Полезное
Смотреть что такое «Рекуррентная формула» в других словарях:
рекуррентная формула — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN recurrence formularecursion formula … Справочник технического переводчика
рекуррентная формула — rekurentinė formulė statusas T sritis fizika atitikmenys: angl. recurrence formula vok. Rekursionsformel, f rus. рекуррентная формула, f pranc. formule de récurrence, f … Fizikos terminų žodynas
Рекуррентная формула — (от лат. recurrens, родительный падеж recurrentis возвращающийся) формула приведения, формула, сводящая вычисление n го члена какой либо последовательности (чаще всего числовой) к вычислению нескольких предыдущих её членов. Обычно эти… … Большая советская энциклопедия
РЕКУРРЕНТНАЯ ТОЧКА — д и н а м и ч е с к о й с и с т е м ы точка хдинамич. системы ft (или, в иных обозначениях, f(t,.), см. [2]), заданной на метрич. пространстве S, удовлетворяющая условию: для всякого e>0 найдется T>0 такое, что все точки траектории ftx… … Математическая энциклопедия
Математическая формула — Эта статья об обозначениях элементарной математики; Для более общего контекста см.: Математические обозначения. Математическая формула (от лат. formula уменьшительное от forma образ, вид) принятая в математике (а также… … Википедия
Решение рекуррентных соотношений
Содержание
Определения [ править ]
[math] F_0 = 0,\qquad F_1 = 1,\qquad F_
Для этого можно использовать метод производящих функций (англ. generating function method).
Метод производящих функций [ править ]
Примеры [ править ]
[math]1[/math] пример [ править ]
Производящие функции позволяют решать рекуррентные соотношение механически по одному и тому же алгоритму. Рассмотрим общую схему на простом примере, который позволит продемонстрировать базовые приёмы работы.
Задано линейное однородное рекуррентное соотношение порядка [math]2[/math] с постоянными коэффициентами:
[math]\begin
Будем искать производящую функцию последовательности в виде
[math] G(z)=\displaystyle\sum_
Теперь сложим все уравнения для всех значений [math]n[/math] :
[math] \underbrace
Аналогичные манипуляции со второй суммой дают нам выражение
[math] \displaystyle\sum_
откуда получаем производящую функцию последовательности в замкнутом виде:
[math] G(z) = \dfrac
Теперь разобьём дробь на сумму простых дробей:
[math] \dfrac
Из этого разложения следует, что
[math] \dfrac<1><1-3z>= \displaystyle\sum_
С другой стороны, мы искали [math]G(z)[/math] в виде
[math] G(z)=\displaystyle\sum_
поэтому, в силу равенства рядов, [math]a_n=3^n-2^n[/math] (для [math]n\geqslant 0[/math] ).
[math]2[/math] пример: числа Фибоначчи [ править ]
Рассмотрим рекуррентное соотношение для чисел Фибоначчи:
[math]\begin
Первый шаг алгоритма мы уже выполнили, записав рекуррентное соотношение. Выполним второй шаг:
[math]\begin
Складываем все строчки:
[math] f_0 + f_1 z + \displaystyle\sum_
Третий шаг алгоритма требует привести все суммы к замкнутому виду:
[math]\begin
откуда получаем замкнутое выражение для производящей функции:
[math] G(z) = \dfrac
Осталось разложить её в ряд (чего требует четвёртый шаг алгоритма). С этой целью нужно разложить знаменатель на множители. Найдем корни уравнения:
[math]\displaylines< 1-z-z^2 = 0 \cr z_1=-\dfrac<1-\sqrt<5>><2>, z_2=-\dfrac<1+\sqrt<5>><2>. > [/math]
Нам известно разложение следующей рациональной функции:
[math] \dfrac<1> <1-z>= \displaystyle\sum_
Рассмотрим первую дробь и поделим в ней числитель и знаменатель на [math]z_1[/math] :
[math] \dfrac
Аналогично (но с делением на [math]z_2[/math] ) поступим со второй дробью:
[math] \dfrac
[math]3[/math] пример [ править ]
Рекуррентное соотношение:
[math] \begin
[math]4[/math] пример [ править ]
Рассмотрим следующее рекуррентное соотношение:
[math]\begin
Вспомним, что
[math] (z^n)’ = nz^
поэтому
[math] \displaystyle\sum_
Последняя сумма может быть свёрнута:
[math] \displaystyle\sum_
Подставив свёрнутое выражение обратно, имеем,
[math] z\biggl(\displaystyle\sum_
Это уравнение для производящей функции. Из него выражаем [math]G(z)[/math] :
[math] G(z) = \dfrac<1-6z+11z^2-5z^3><(1-6z+8z^2)(1-z)^2>. [/math]
Дальше мы знаем что делать со всеми этими дробями, кроме, разве лишь, первой. Рассмотрим её (без множителя) подробнее:
[math] \dfrac<1> <(1-z)^2>=(1-z)^ <-2>=\displaystyle\sum_
Рекуррентные соотношения и уравнения
В этом разделе вы найдете бесплатные примеры решений рекуррентных соотношений методом характеристического уравнения и подбора частного решения по правой части. Также приведены краткие алгоритмы решения для двух методов и пример их использования для последовательности Фибоначчи.
Как решать рекуррентные соотношения?
Для решения рекуррентных соотношений применяют один из двух основных способов:
В следующем разделе мы сравним, как выглядит процесс решения для одной и той же последовательности двумя методами.
Метод производящих функций
Метод характеристических функций
Этот метод практически полностью аналогичен методу решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, кратко алгоритм выглядит так:
Решение для последовательности чисел Фибоначчи
Общая формула данной рекуррентной последовательности имеет вид6
Способ 1. Производящяя функция
$$\begin
Складываем все строчки:
На третьем шаге алгоритма приводим все суммы к замкнутому виду:
откуда выводим искомое выражение для производящей функции:
Теперь разложим ее в степенной ряд. Для этого сначала разложим знаменатель на множители. Найдем корни уравнения:
Чтобы разложить данные дроби в ряды, используем известное разложение для дроби:
Преобразуем данное выражение, используя то, что
Способ 2. Характеристическое уравнение
Тогда общее решение однородного рекуррентного уравнения имеет вид:
Решая систему, найдем
Итоговое выражение для последовательности чисел Фибоначчи:
Результаты обоих методов совпали, решение вторым методом оказалось проще и короче.
Примеры решений
Что значит «рекуррентная формула»
Энциклопедический словарь, 1998 г.
Большая Советская Энциклопедия
Последовательность jn ≈ т. н. чисел Фибоначчи ≈ задаётся формулами:
j0 = 0, j1 = 1, jn+2 = jn+1 + jn (n > 0)
Последняя из них является Р. ф.; она позволяет вычислить j2, j3 и дальнейшие члены этой последовательности.
Нетрудно показать, что для n ³ 2 выполняется соотношение
Это ≈ Р. ф., сводящая вычисление In к вычислению /0 или l1 в зависимости от чётности n.
Р. ф. обычно даёт удобную вычислительную схему для нахождения членов последовательности друг за другом. Однако иногда, исходя из Р. ф., стремятся получить «явное» выражение для n-го члена последовательности, описываемой этой Р. ф. Так, в случае чисел Фибоначчи
Википедия
Рекуррентная формула — формула вида a = f(n, a, a, …, a), выражающая каждый член последовательности a через p предыдущих членов и возможно номер члена последовательности n.
Рекуррентным уравнением называется уравнение, связывающее несколько подряд идущих членов некоторой числовой последовательности. Последовательность, удовлетворяющая такому уравнению, называется рекуррентной последовательностью.
Транслитерация: rekurrentnaya formula
Задом наперед читается как: алумроф яантнеррукер
Рекуррентная формула состоит из 19 букв