Что значит разность векторов

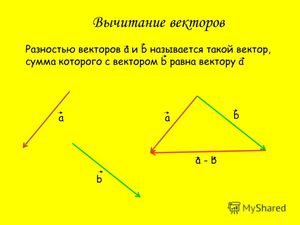
Определение разности двух векторов

В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
[block >

Определения векторной математики

Введём главные определения, используемые при выполнении линейных операций.

Аналитический метод

Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.

Для двухмерного пространства и векторных величин a <a₁; a₂> и b <b₁; b₂> расчёты будут иметь следующий вид: c <c₁; c₂> = <a₁ — b₁; a₂ — b₂>.

В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a <a₁; a₂; a₃> и b <b₁; b₂; b₃> координаты разности будут также получены попарным вычитанием: c <c₁; c₂; c₃> = <a₁ — b₁; a₂ — b₂; a₃ — b₃>.

Вычисление разности графически

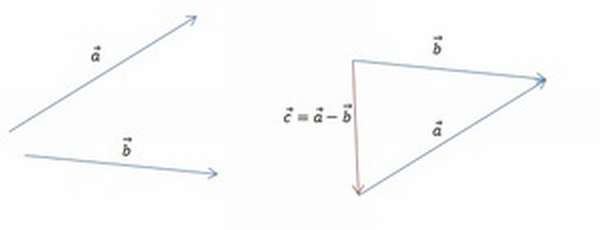
Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:

[block > Результат операции вычитания показан на рисунке ниже.

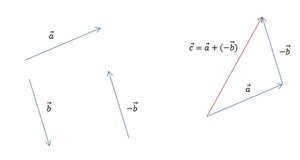
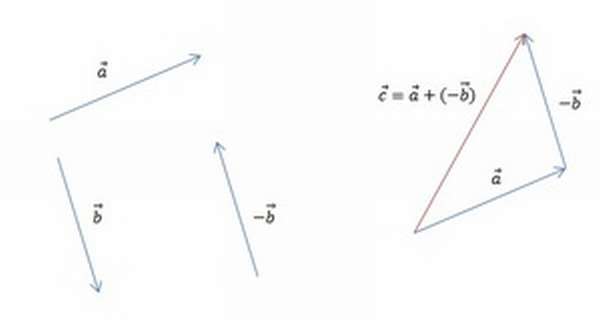
Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:

Результат такого решения изображён на рисунке:

Решение задач

Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.

Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.

Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:

Аналогичный расчёт выполняется для CD:

Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид <c₁; c₂> = <a₁ — b₁; a₂ — b₂>. Для конкретного случая можно записать:

Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
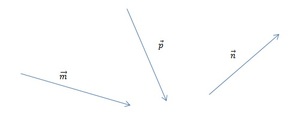
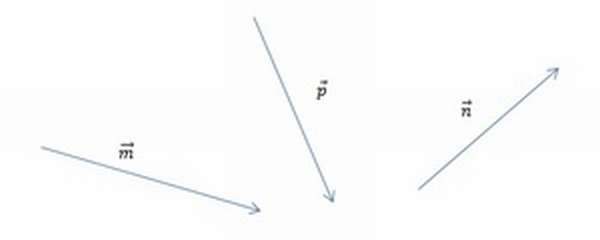
[block > Задача 2. На рисунке изображены векторы m, n и p.

Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.

Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.

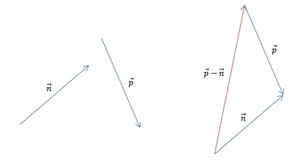
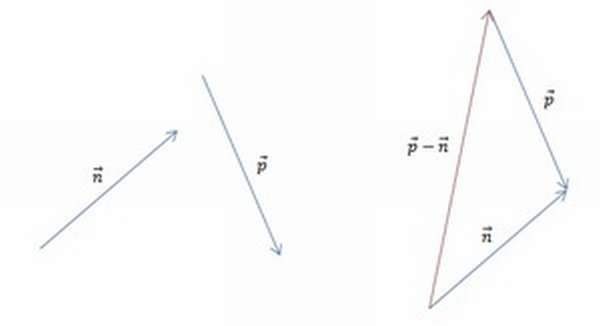
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.

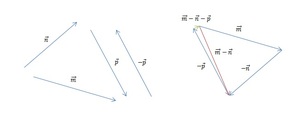
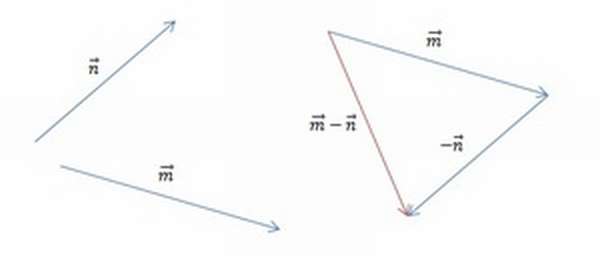
Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:

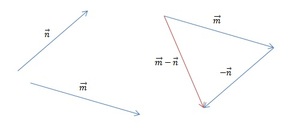
[block > Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:

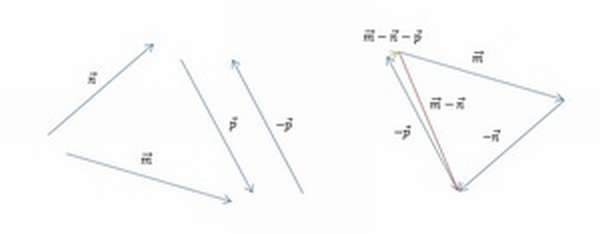
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).

Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
[block > [block >

Источник

Определение разности двух векторов

В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.

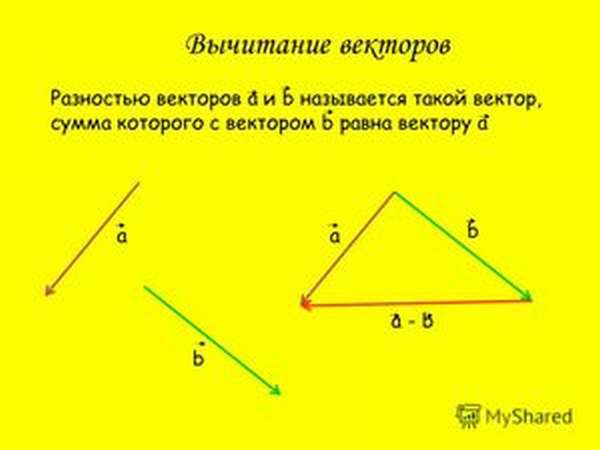
Максимально наглядно применение векторных величин объясняется в физике. Самыми простыми примерами являются силы (сила трения, сила упругости, вес), скорость и ускорение, поскольку помимо численных значений они также обладают направлением действия. Для сравнения приведём пример скалярных величин: это может быть расстояние между двумя точками или масса тела. Для чего же необходимо выполнять действия над векторными величинами такие как сложение или вычитание? Это нужно, чтобы было возможно определить результат действия системы векторов, состоящей из 2 или более элементов.

Определения векторной математики

Введём главные определения, используемые при выполнении линейных операций.

Аналитический метод

Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.

Для двухмерного пространства и векторных величин a и b расчёты будут иметь следующий вид: c = .

В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a и b координаты разности будут также получены попарным вычитанием: c = .

Вычисление разности графически

Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:

Результат операции вычитания показан на рисунке ниже.

Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:

Результат такого решения изображён на рисунке:

Решение задач

Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.

Задача 1. На плоскости заданы 4 точки: A (1, —3), B (0, 4), C (5, 8), D (—3, 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.

Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1, —3), а концом B (0, 4). Рассчитаем координаты направленного отрезка:

Аналогичный расчёт выполняется для CD:

Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид = . Для конкретного случая можно записать:

Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.

Задача 2. На рисунке изображены векторы m, n и p.

Необходимо построить для них разности: p — n, m — n, m — n — p. Выяснить, какая из них обладает наименьшим модулем.

Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.

Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.

Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:

Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:

Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).

Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.

Источник

Векторы на ЕГЭ по математике. Действия над векторами

Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?

А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.

Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».

Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.

Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:

Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: или

До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.

Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.

Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.

Если координаты вектора заданы, его длина находится по формуле

Сложение векторов

Для сложения векторов есть два способа.

Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.

По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.

При сложении векторов и получаем:

Вычитание векторов

Вектор направлен противоположно вектору . Длины векторов и равны.

Теперь понятно, что такое вычитание векторов. Разность векторов и — это сумма вектора и вектора .

Умножение вектора на число

При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля.

Скалярное произведение векторов

Векторы можно умножать не только на числа, но и друг на друга.

Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.

Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:

Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов и :

Из формулы для скалярного произведения можно найти угол между векторами:

Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.

В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.

Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.

Онлайн-курс «Математика 10+11 100 баллов»

— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.

Источник

Вычитание векторов. Как найти разность векторов

Как сложить и вычесть векторы с помощью онлайн-калькулятора

Чтобы сложить или вычесть векторы при помощи онлайн калькулятора, достаточно лишь задать необходимые векторы. Для этого:

В рассматриваемом примере, оставим размерность «2». То есть, мы работаем с векторами на плоскости.

Для наглядности, зададим один вектор точками, а второй – координатами.

Вычитание векторов. Правило второе

Вспомним следующее необходимое нам понятие.

Для того чтобы ввести второе правило для разности двух векторов, нам необходимо в начале ввести и доказать следующую теорему.

Доказательство.

По определению 2, имеем

Теорема доказана.

Правило параллелограмма разности векторов

Если два неколлинеарных вектора и имеют общее начало (рис. 3), то разностью этих вектор есть вектор, совпадающий с диагональю параллелограмма, построенного на этих векторах и , причем начало этой диагонали совпадает с концом вектора , а конец – с концом вектора .

Если векторы и заданы своими координатами в некотором базисе: , то, чтобы найти координаты их разности , необходимо от координат вектора отнять соответствующие координаты вектора :

Основные правила вычисления

Для того, чтобы найти значение разности векторов, можно использовать несколько способов.

Правило треугольника

Правило параллелограмма

Если векторы \(\overrightarrow а\) и \(\overrightarrow b\) заданы в некотором промежутке:

\(\overrightarrow a=\left(а_1;а_2\right),\;\overrightarrow b=\left(b_1;b_2\right)\)

\(\overrightarrow a\;-\;\overrightarrow b=\left(a_1;a_2\right)-\left(b_1;b_2\right)=\left(a_1-b_1;a_2-b_2\right)\)

Проиллюстрируем правило многоугольника:

Аналитический метод

Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.

Для двухмерного пространства и векторных величин a <a₁; a₂> и b <b₁; b₂> расчёты будут иметь следующий вид: c <c₁; c₂> = <a₁ — b₁; a₂ — b₂>.

В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a <a₁; a₂; a₃> и b <b₁; b₂; b₃> координаты разности будут также получены попарным вычитанием: c <c₁; c₂; c₃> = <a₁ — b₁; a₂ — b₂; a₃ — b₃>.

Решение задач

Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.

Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.

Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:

Аналогичный расчёт выполняется для CD:

Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид <c₁; c₂> = <a₁ — b₁; a₂ — b₂>. Для конкретного случая можно записать:

Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06. [block Задача 2. На рисунке изображены векторы m, n и p.

Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.

Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.

Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.

Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:

[block Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:

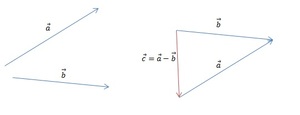
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).

Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p. [block [block >

Источник