Что значит растянуть график
График функции y=f(kx)
Растяжение и сжатие — один из видов геометрических преобразований, благодаря которому на основе графиков элементарных функций можно легко строить графики многих других функций.
График функции y=f(kx) (где k>1) может быть получен из графика функции y=f(x) сжатием к оси Oy в k раз.
При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x/k; y) графика y=f(kx):
(то есть абсциссу (x) каждой точки начального графика уменьшаем в k раз, а ординату (y) оставляем без изменения. При этом точка, лежащая на оси Oy, остаётся на месте (так как 0:k=0).
1) График функции y=(2x)² можно получить из графика функции y=x ² с помощью сжатия к оси Oy в 2 раза.
На координатной плоскости строим график функции y=x² (можно отметить только его базовые точки). Затем координату x каждой точки делим на 2, а координату y оставляем без изменения. Таким образом, каждая точка нового графика становится ближе в 2 раза к оси Oy, чем точка начального графика (от оси Ox обе точки находятся на одинаковом расстоянии):
График y=(2x)² из графика y=x²
2) График функции y=√(5x) можно получить, сжав график функции y= √ x к оси Oy в 5 раз:
3) График функции y=|4х| может быть получен из графика функции y=|х| сжатием к оси Oy в 4 раза:
Преобразование графиков применяется при решении примеров из различных разделов алгебры.
Преобразование графиков элементарных функций
Основные элементарные функции в чистом виде без преобразования встречаются редко, поэтому чаще всего приходится работать с элементарными функциями, которые получили из основных с помощью добавления констант и коэффициентов. Такие графики строятся при помощи геометрических преобразований заданных элементарных функций.
Геометрические преобразования графика функции
Существует 3 вида геометрических преобразований графика:
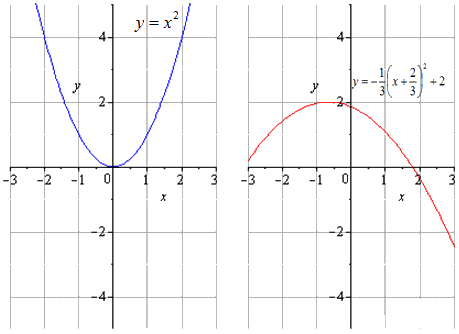
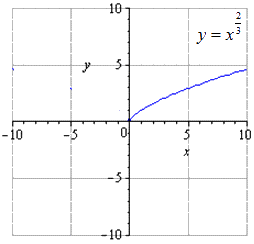
Степенная функция
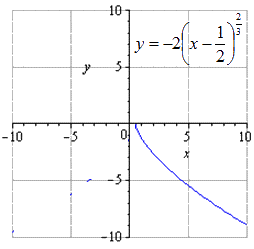
Рассмотрим решения на примерах, начиная со степенной функции.
Представим функции таким образом:
Если изобразить исходную степенную функцию, получим, что
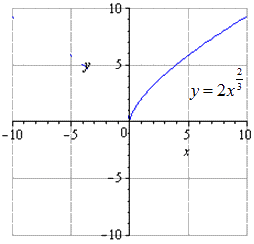
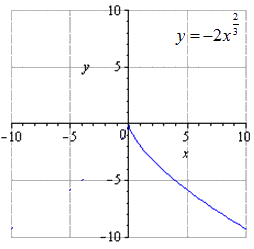
при растягивании вдвое вдоль О у имеем, что
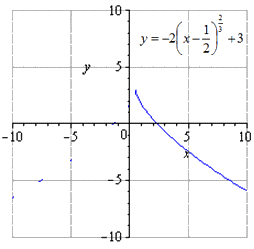
а движение вправо на 1 2
движение на 3 единицы вверх имеет вид
Показательная функция
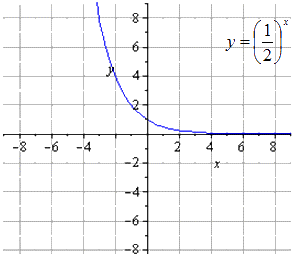
Преобразования показательной функции рассмотрим на примерах.
Преобразуем функцию, исходя из свойств степенной функции. Тогда получим, что
Отсюда видно, что получим цепочку преобразований y = 1 2 x :
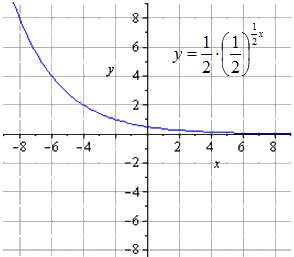
Получаем, что исходная показательная функция имеет вид
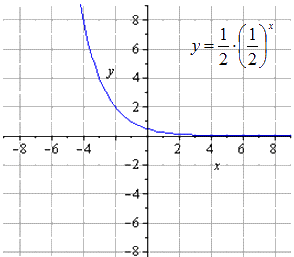
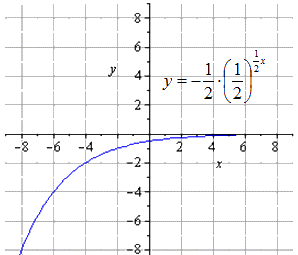
Сжимание вдвое вдоль О у дает
Растягивание вдоль О х
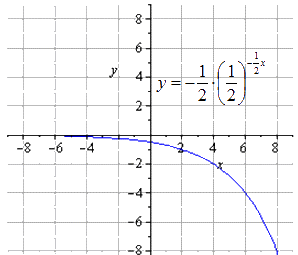
Симметричное отображение относительно О х
Отображение симметрично относительно О у
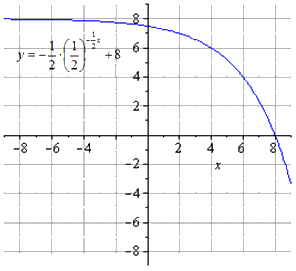
Сдвигание на 8 единиц вверх
Логарифмическая функция
Для решения необходимо использовать свойства логарифма, тогда получаем:
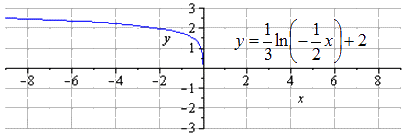
Преобразования логарифмической функции выглядят так:
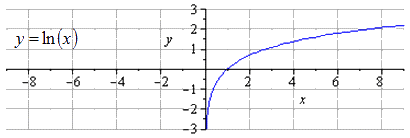
Изобразим график исходной логарифмической функции
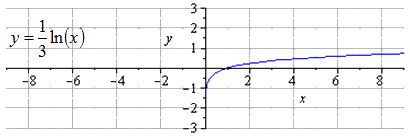
Производим сжимание строе по О у
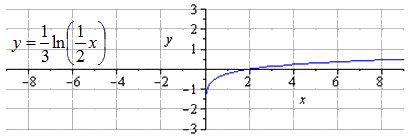
Производим растягивание вдоль О х
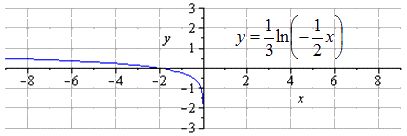
Производим отображение относительно О у
Производим сдвигание вверх на 2 единицы, получаем
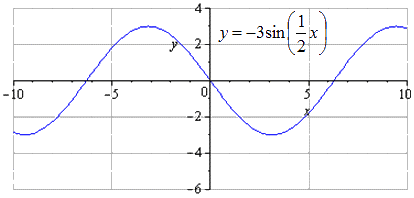
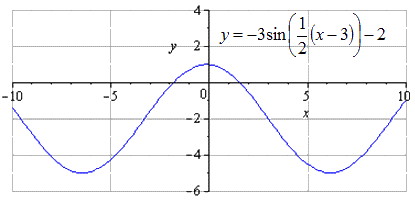
Преобразования y = sin x
На данном этапе график тригонометрической функции считается преобразованным.
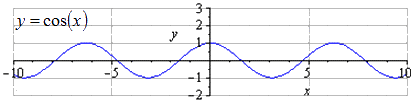
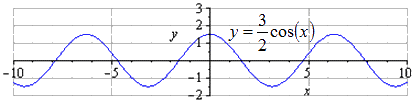
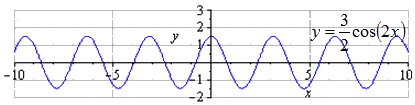
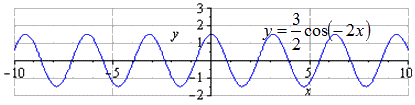
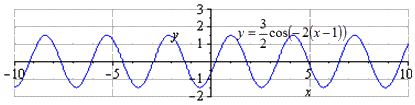
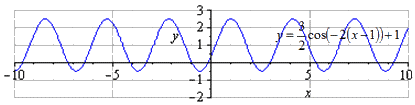
Преобразование функции y = cos x
Отсюда получаем, что получится график тригонометрической функции вида:
Пошаговое преобразование косинусоиды с графической иллюстрацией.
Преобразования функции косинуса завершено.
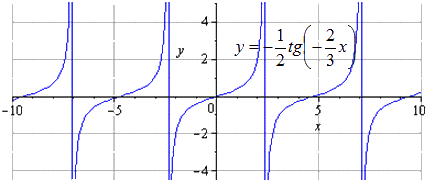
Преобразования y = tgx
Поэтапное преобразование тангенсоиды с графическим изображением.
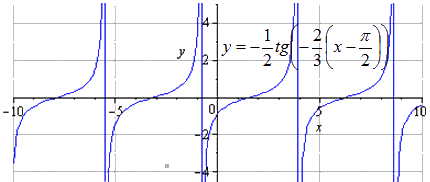
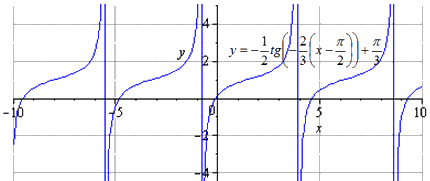
При сдвигании графика на π 3 получаем, что изменение области определения отсутствует.
Преобразование тангенса завершено.
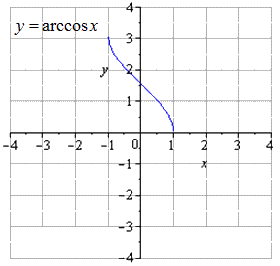
Тригонометрическая функция вида y = a r c cos x
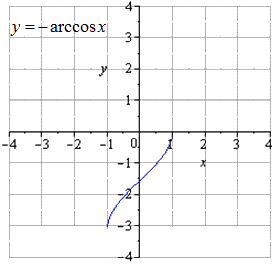
Поэтапное преобразование арккосинуса и графическое изображение.
График, данный по условию
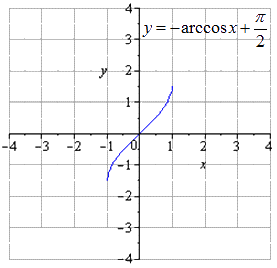
Производим отображение относительно О х
Таким образом, осуществляется переход от арккосинуса к косинусу. Необходимо произвести геометрические преобразования арксинуса и его графика.
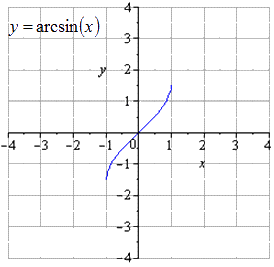
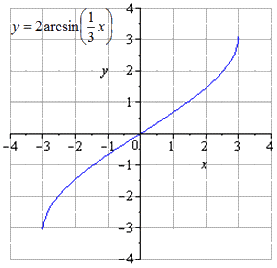
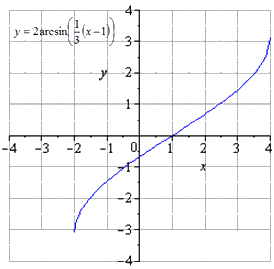
Отсюда получаем, что преобразования y = a r c sin x примет вид:
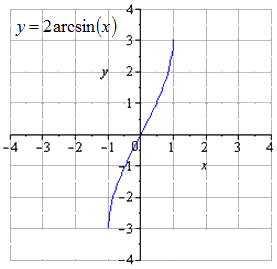
Поэтапное преобразование графика арксинуса и графическое изображение.
Задача преобразования графика обратной тригонометрической функции завершена. Если по условию имеются сложные функции, тогда необходимо прибегнуть к полному исследованию функция.
Преобразования графиков тригонометрических функций
Общие принципы преобразования графиков функций изучались нами в главе 8, (см. §47, §48, §50 справочника для 8 класса). В этом параграфе мы рассмотрим особенности тригонометрических функций при использовании этих преобразований.
п.1. Растяжение и сжатие графиков тригонометрических функций по оси OX
Общие принципы растяжения и сжатия графиков по оси OX:
Эти принципы справедливы и для тригонометрических функций.
Тригонометрические функции являются периодическими: синус и косинус с периодом 2π, тангенс и котангенс – с периодом π. Получаем следствие общих принципов:
п.2. Растяжение и сжатие графиков тригонометрических функций по оси OY
Общие принципы растяжения и сжатия графиков по оси OY:
Общий принцип сжатия графиков:
Эти принципы справедливы и для тригонометрических функций.
Т.к. для графиков синуса и косинуса (синусоиды) характерна амплитуда колебаний, то также говорят, что:
п.3. Параллельный перенос графиков тригонометрических функций по оси OX
Общие принципы переноса по оси OX:
Эти принципы справедливы и для тригонометрических функций.
При этом параметр x называют начальной фазой колебаний.
При сравнении двух тригонометрических функций \(y_1=f(x)\) и \(y_2=f(x\pm a)\) говорят, что у второй функции сдвиг по фазе равен \(\pm a\).
п.4. Параллельный перенос графиков тригонометрических функций по оси OY
Общие принципы переноса по оси OY:
Эти принципы справедливы и для тригонометрических функций.
п.5. Общее уравнение синусоиды
График \(y(x)=Acos(cx+d)+B\) также называют синусоидой. Термин «косинусоида» употребляется относительно редко.
Поскольку график косинуса получается из графика синуса сдвигом по фазе на π/2 влево, вводить термин «косинусоида» излишне.
Построим график \(g(x)=3sin\left(2x+\frac\pi2\right)-1\)
По сравнению с \(f(x)=sinx\):
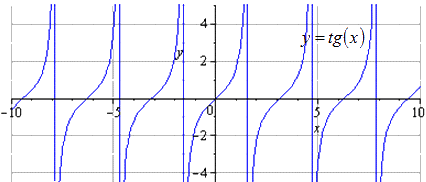
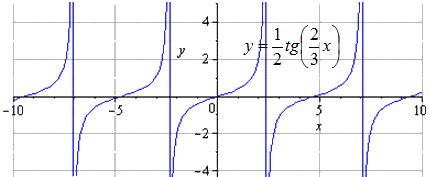
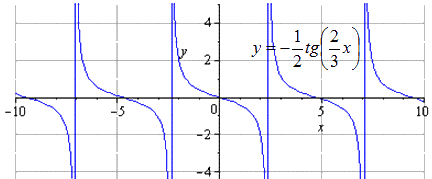
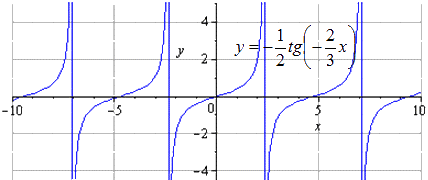
п.6. Общее уравнение тангенцоиды
График \(y(x)=Actg(cx+d)+B\) также называют тангенцоидой.
Построим график \(g(x)=\frac12 tg\left(\frac
По сравнению с \(f(x)=tgx\):
п.7. Примеры
Пример 2. Найдите наименьшие положительные периоды функций:
a) \(y=sin5x\)
Период синуса \(2\pi\) уменьшается в 5 раз. Получаем: \(T=\frac<2\pi><5>\)
б) \(y=cos\pi x\)
Период косинуса \(2\pi\) уменьшается в \(\pi\) раз. Получаем: \(T=\frac<2\pi><\pi>=2\)
в) \(y=tg\frac
Период тангенса \(\pi\) увеличивается в 4 раза. Получаем: \(T=4\pi\)
г) \(y=tg\left(2x+\frac<\pi><3>\right)\)
Период тангенса \(\pi\) уменьшается в 2 раза. Получаем: \(T=\frac\pi2\)
Пример 4. Определите графически, сколько корней имеет уравнение на отрезке: a) \(sinx=sin2x\) при \(0\leq x\leq 3\pi\)
Ответ: 7 корней
б) \(cos\frac
Ответ: 7 корней
Растяжение и сжатие графиков функций
Список функций, изученных в 7 и 8 классе
Растяжение и сжатие графика по оси OX
Сравним графики пар функций, которые в общем виде можно записать так:
$y_2 = y_1 при x_2 = \frac<1> <2>x_1$
График сжимается в 2 раза по оси OX

График сжимается в 2 раза по оси OX
$y_2=y_1 при x_2 = \frac<1> <2>x_1$
График сжимается в 2 раза по оси OX
Теперь сравним пары функций с делением на p:
$ y_2 = f \left(\frac
$y_2 = y_1 при x_2 = 2x_1$
График растягивается в 2 раза по оси OX

$y_2 = f \left(\frac
$ y_2 = y_1 при x_2 = 2x_1$
График растягивается в 2 раза по оси OX
$y_2=y_1 при x_2 = 2x_1$
График растягивается в 2 раза по оси OX
При сравнении графиков двух функций
график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций
график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Растяжение и сжатие графика по оси OY
Сравним графики пар функций, которые в общем виде можно записать так:
$y_2 = 2y_1 при x_2 = x_1$
График растягивается в 2 раза по оси OY

$ y_2 = 2y_1 при x_2 = x_1$
График растягивается в 2 раза по оси OY
$y_2 = 2y_1 при x_2 = x_1$
График растягивается в 2 раза по оси OY
Теперь сравним пары функций с делением на A:
$y_2 = \frac<1><2>y_1 при x_2 = x_1$
График сжимается в 2 раза по оси OY

$ y_2 = \frac<1><2>y_1 при x_2 = x_1$
График сжимается в 2 раза по оси OY
$y_2 = \frac<1><2>y_1 при x_2 = x_1$
График сжимается в 2 раза по оси OY
При сравнении графиков двух функций
график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.
При сравнении графиков двух функций
график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Примеры
Пример 1. Постройте в одной координатной плоскости графики функций:
Пример 2*. Постройте в одной координатной плоскости графики функций:
Памятка «Преобразование графиков функций»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ ОРЕНБУРГСКОЙ ОБЛАСТИ
Государственное автономное профессиональное образовательное
учреждение «Бузулукский строительный колледж»
г. Бузулука Оренбургской области
Выполнил: студент группы № 14 Поршин Артем,
ПАМЯТКА
«Алгоритм преобразования графиков функций – растяжение и сжатие вдоль осей координат»
Сжатие (растяжение) графика к (от) оси ординат.
Сначала изобразим график синуса, его период равен: T = 2π
Мысленно возьмём синусоиду в руки и сожмём её к оси Oy в 2 раза:
То есть, график функции y = sin 2 x получается путём сжатия графика y = sin x к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился: T = π
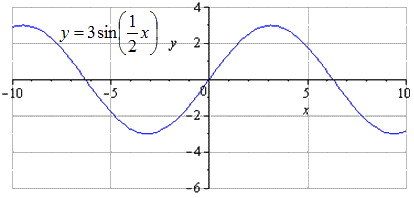
2. Растяжение графика функции от оси ординат
Пример 2. Построить график функции
Берём в руки нашу «бесконечную гармошку»:
И растягиваем её от оси Oy в 2 раза:
То есть, график функции получается путём растяжения графика y = sin x от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза: T = 4π.
Сжатие (растяжение) графика к (от) оси абсцисс
1. Если ФУНКЦИЯ f ( x ) умножается на число m >1, то происходит растяжение её графика вдоль оси ординат.
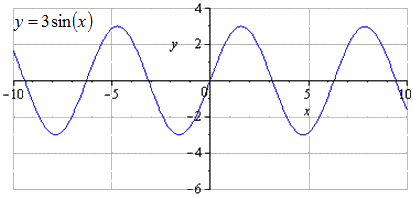
Пример 3 Построить график функции y = 2 sin x .
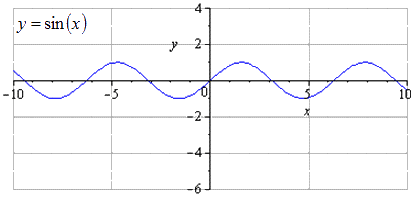
Рисуем график функции y = sin x
А теперь вытягиваем её вдоль оси Оу в 2 раза:
Период функции y = 2 sin x не изменился и составляет Т = 2π, а вот значения (все, кроме нулевых) увеличились по модулю в два раза, что логично – ведь функция умножается на 2, и область её значений удваивается: Е = [-2; 2].
2. Если ФУНКЦИЯ умножается на число 0 m
Пример 4. Построить график функции y = sin x
Рисуем график функции y = sin x
Теперь сожмём синусоиду вдоль оси Оу в 2 раза:
Аналогично, период Т = 4π не изменился, но область значений функции «сплющилась» в два раза:
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-907273
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Росприроднадзор призвал ввести в школах курс по экологии
Время чтения: 1 минута
Минпросвещения планирует выделить «Профессионалитет» в отдельный уровень образования
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
НИУ ВШЭ откроет первую в России магистратуру по управлению низкоуглеродным развитием
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.