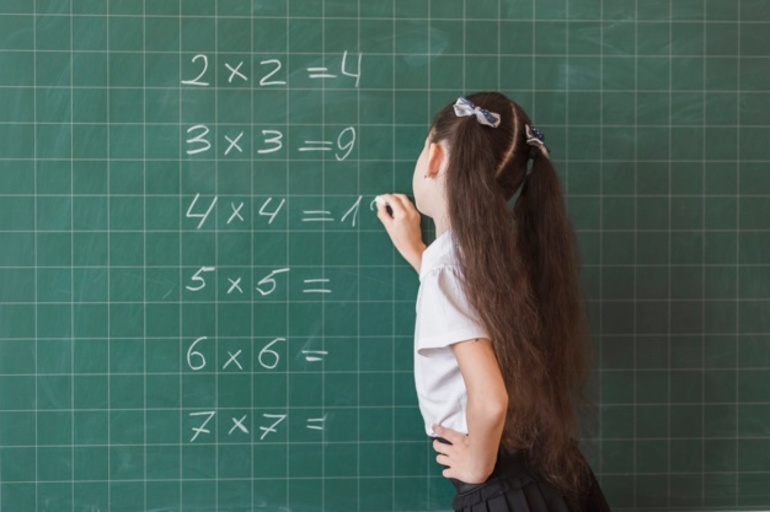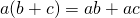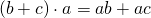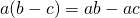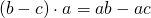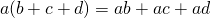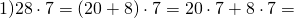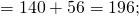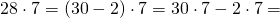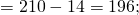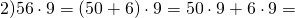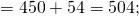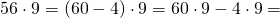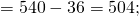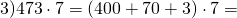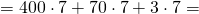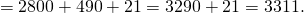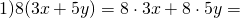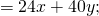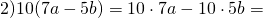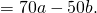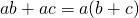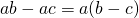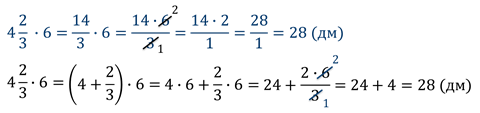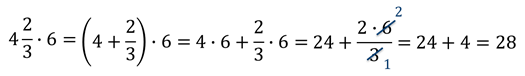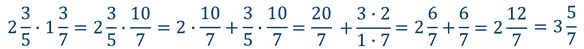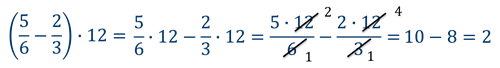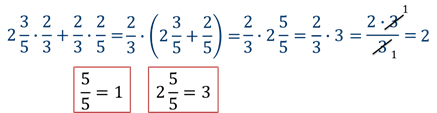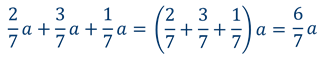Что значит распределительное свойство умножения
Краткое описание
Используемый в школе распределительный закон умножения позволяет ученикам максимально быстро выполнить все необходимые вычисления. Знание определенных нюансов поможет решить сложные уравнения и различные задачи. Процесс умножения представляет собой сокращенный процесс сложения. А это означает, что первый множитель выступает в роли числа, которое складывается само с собой определенное количество раз, соответствующее второму множителю. Пример: 4 * 8 = 4+4+4+4+4+4+4+4 = 32.
Элементарное математическое умножение было изобретено в то время, когда у человечества возникла необходимость выполнять большие вычисления, которые просто неудобно записывать в виде элементарного сложения. Всем хорошо известно, что можно 8 раз сложить число 4, а можно 4 раза сложить число 8, но итоговый результат от этого не поменяется. Именно в этом и состоит смысл переместительного умножения всех задействованных элементов. Умножение позволило человеку решить довольно много проблем, но вместе с этим в алгебру пришло и деление, но уже как противоположная математическая операция.
Ключевые особенности
Чтобы даже на начальном этапе ученик мог выполнить умножение суммы некоторых чисел, необходимо просто умножить каждое слагаемое по отдельности и сложить полученный результат. К примеру: (j + d) * s = sj + sd либо s * (j + d) = sj + sd. Чтобы немного упростить способ решения задачи, описанное правило можно использовать в обратном порядке: s * j + s * d = s * (j + d). В этом случае общий множитель выносится за пределы скобок.
Если попробовать задействовать многофункциональное распределительное свойство сложения, то в итоге можно будет решить следующие математические примеры:
Умелое применение распределительного свойства умножения поможет избежать распространенных ошибок. Так, основное правило актуально не только по отношению к сумме, но и к разности двух и более выражений. Для укрепления полученных навыков можно попробовать самостоятельно придумать задачу.
Основные математические возможности
Чтобы можно было выполнить определенные арифметические действия по отношению к числу, необходимо поочередно умножить его на каждое слагаемое и в итоге сложить полученные произведения. А это значит, что для любых частных чисел l, r, w верным будет следующее равенство: w * (l + r) = w * l + w * r. Этот пример отлично выражает распределительный закон сложения и последующего умножения. Так как число и сумма являются множителями, то после смены их места расположения, задействовав для этого переместительное свойство, можно будет сформировать наиболее подходящее свойство.
Всего специалисты выделяют три свойства распределительного умножения:
Все перечисленные направления имеют свои особенности и правила использования на практике, которые обязательно нужно учесть для лучшего усвоения этой темы.
Правила вычитания
Умножение и последующее вычитание натуральных чисел обязательно связывается распределительным свойством. Учащимся обязательно нужно запомнить формулировку этого правила: умножить определенную разность двух рациональных чисел на конкретное число — это вычитание из произведения уменьшаемого числа произведения данного или неизвестного вычитаемого числа. Все математические примеры записываются при помощи обычных букв: (s — r)* n = s * n — r * n. Задействованными символами могут называться определенные рациональные целые и дробные числа.
Элементарные примеры распределительного свойства умножения позволяют ученикам освоить технику решения распространенных математических задач. Если необходимо убедиться в равенстве уравнения 5 * (8 — 3) = 5 * 8 — 5 * 3, тогда нужно выполнить несколько арифметических действий. Так как пример 8 − 3 всегда равен 5, то произведение 5 * (8 — 3) всегда будет иметь следующий результат: 5 * 5 = 5+5+5+5+5=25. Теперь нужно вычислить разность между 5 * 8 и 5 * 3. Решение выглядит следующим образом: 5 * 8 − 5 * 3 = (5+5+5+5+5+5+5+5) — (5+5+5) = 40 — 15 = 25. Это значит, что равенство 5 * (8 − 3) = 5 * 8 − 5 * 3.
Использование двух и более слагаемых
Распространенное в алгебре распределительное свойство элементарного умножения активно применяется не только по отношению к двум слагаемым, но и для неограниченного количества арифметических элементов. Этот подход можно применить для всех форм дробей, что очень удобно. Стандартная формула имеет следующий вид:
В качестве примера следует рассмотреть следующее уравнение: 678 * 4. Чтобы понять все нюансы, надо представить число 678 как сумму трех чисел: 600, 70 и 8. Если это сделать, то в итоге можно получить следующее решение: (600 + 70 + 8) * 4 = 600 * 4 + 70 * 4 + 8 * 4 = 2400 + 280 + 32 = 2712. Для более быстрого решения задачи нужно упростить несколько выражений, используя для этого упомянутое ранее свойство.
Если в качестве примера взять уравнение 8 * (4х + 3у), тогда первым делом раскрывают имеющиеся скобки, применяя для этого распределительный закон умножения: 8 * 4х + 8 * 3у = 32х + 24у. Конечно, полученный результат сложить просто невозможно, так как заявленные слагаемые не являются подобными, к тому же они имеют разную буквенную часть. Именно поэтому ответ будет выглядеть следующим образом: 32х + 24у.
Если ученик научится использовать при решении различных примеров универсальное распределительное свойство сложения и умножения, то в итоге он сможет легко решать даже самые сложные математические примеры, так как многие ситуации можно свести к устному счету. Также будет существенно экономиться время при решении многоуровневых задач. Благодаря полученным знаниям, можно будет с легкостью упростить выражения. Эксперты рекомендуют дважды проверять выполненную работу, так как только в этом случае можно будет избежать ошибок.
Умножение нуля
Несмотря на то что ноль не относится к категории естественных чисел, этому направлению тоже нужно уделить повышенное внимание. Это связано с тем, что такое свойство используется во время умножения натуральных чисел столбиком. Если строго соблюдать смысл умножения, тогда произведение 0 * х, где х выступает в роли произвольного естественного числа больше единицы, представляет собой сумму х слагаемых. В такой ситуации актуальной является следующая формула: 0 * х = 0+0+0+0+….+0. Свойства математического сложения позволяют специалистам утверждать, что последняя сумма неизбежно будет равна нулю.
Чтобы иметь возможность сохранить справедливость элементарного умножения используемого числа на единицу, можно считать верным следующее равенство: 0 * 1 = 0. Это значит, что для любого естественного числа х выполняется равенство 0 * х = 0. Чтобы оставалось актуальным переместительное свойство умножения, нужно помнить о справедливости равенства х * 0 = 0 для всех натуральных чисел х.
Произведение естественного числа и нуля равно нулю 0 * х = 0, а также х * 0 = 0. Используемый x представляет собой произвольное натуральное число. Экспертами было доказано, что последнее утверждение играет важную роль формулировки свойства умножения ранее полученного числа и нуля. К примеру, произведение чисел 87 и 0 равно нулю. Если попробовать умножить 0 на 897689, то в итоге тоже получим ноль.
Распределительное свойство относительно разности
Понять все нюансы помогут следующие три примера:
Решать такие задачи элементарно и быстро, но для этого нужно хорошо усвоить все правила, а также рекомендации специалистов, так как только в этом случае можно будет избежать грубых ошибок.
Манипуляции с натуральным числом
Этот раздел связан с умножением единицы на конкретное число. Если следовать смыслу умножения, то в итоге произведение изучаемого арифметического выражения х будет равно сумме х слагаемых, каждое из которых тоже равно единице. Действует элементарная формула: 1 * х = 1+1+1+….+1 = х. Пример: произведение чисел 1 и 78 равно 78, а результатом умножения 1 и 456 есть число 456.
Произведение х * 1 лишено какого-либо смысла, так как это арифметическое выражение представляет собой сумму одного слагаемого, которое равно число х, но сложение определяют для двух и более слагаемых. Чтобы сохранить справедливое переместительное свойство поэтапного умножения, нужно считать верным равенство х * 1 = х.
Опытные математики утверждают, что произведение двух разных чисел, одно из которых приравнивается к нулю, равно другому числу. Это утверждение выступает в качестве официальной формулировки умножения единицы и определенного числа. При помощи букв это свойство записывается так: 1 * х = х * 1 = х. За основу могут использоваться любые натуральные числа.
Многим может показаться, что сегодня нет необходимости разбираться во всех свойствах распределительного умножения, так как под рукой всегда есть калькулятор. Но даже у программ существуют свои ограничения, что просто недопустимо в банковской отрасли и правительственных отраслях. Именно поэтому бухгалтеры в обязательном порядке изучают все особенности применения распределительного закона умножения.
Распределительное свойство умножения

Всего получено оценок: 146.
Всего получено оценок: 146.
Свойства умножения – это, прежде всего, возможность быстро произвести вычисление. Знание распределительного свойства поможет вам без проблем посчитать сложный пример или решить уравнение. Рассмотрим в в подробностях применение распределительного свойства умножения.
Умножение
Умножение – это сокращенный процесс сложения. Что это значит? Первый множитель это число, которое складывается само с собой число раз, равное второму множителю.
3*6=3+3+3+3+3+3=18 – вот как это выглядит на практике. Умножение было изобретено во время, когда потребовались большие вычисления, которые неудобно записывать в виде сложения.
Можно 3 раза сложить число 6, а можно 6 раз сложить число 3. Результат от этого не поменяется, в этом заключается смысл переместительного свойства умножения.
Умножение позволило решить достаточно много проблем, но вместе с ним в математику пришло и деление, как противоположная операция.
Свойства умножения
Всего у умножения 3 свойства:
Распределительное свойство
Распределительно свойство можно использовать для быстрого расчета. Рассмотрим большой пример для 6 класса с применением этого свойства умножения:
Обратите внимание, что пример представляет собой сумму слагаемых, каждый из которых представлен произведением. Рассмотрим каждое произведение в отдельности, а потом сложим результаты.
$$<1\over<2>>*18-<1\over<2>>*16=9-8=1$$ – такие ответы иногда бывают в сложных на вид примерах.
$$(<7\over<3>>+<56\over<3>>)=<63\over<3>>=21$$ – теперь воспользуемся распределительным свойством и умножим число 21 на каждое из чисел в скобках:
1+2+16-1=18 – вот такой маленький ответ получился в большом примере.
При решении этого примера, важно понять, что не всегда нужно использовать распределительное свойство умножения. Важно понимать, когда лучше им воспользоваться, а когда решить другим путем.
Что мы узнали?
Мы узнали, что такое умножение. Поговорили о свойствах умножения и особенно выделили распределительное свойство умножения. Решили большой пример на тему применения этого свойства.
Распределительное свойство умножения
Распределительное свойство умножения — важное правило, полезное в устном счете и при раскрытии скобок.
Распределительное свойство умножения относительно сложения:
Чтобы умножить число на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные результаты сложить.
С помощью букв распределительное свойство умножения относительно сложения записывают так:
Распределительное свойство умножения относительно вычитания:
Чтобы умножить число на разность двух чисел, можно умножить это число на уменьшаемое и на вычитаемое, и из первого произведения вычесть второе.
С помощью букв распределительное свойство умножения относительно вычитания записывают так:
Распределительное свойство умножения верно и для большего количества чисел. Например, для трех слагаемых распределительное свойство умножения относительно сложения имеет вид:
Распределительное свойство умножения упрощает устный счет.
Этот пример можно решить также с помощью распределительного свойства умножения относительно вычитания:
С помощью распределительного свойства умножения можно раскрывать скобки.
(Более подробно тема раскрытия скобок рассматривается после изучения отрицательных чисел).
Распределительное свойство умножения можно применить и в обратном порядке:
Говорят: «Общий множитель a выносим за скобки. В скобках остается b плюс c».
Говорят: «Общий множитель a выносим за скобки. В скобках остается b минус c».
Более подробно вынесение общего множителя за скобки изучают в курсе алгебры 7 класса.
Применение распределительного свойства умножения
Урок 15. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Применение распределительного свойства умножения»
Сегодня на уроке мы вспомним уже известное вам распределительное свойство умножения и применим его при решении задач и примеров.
Для начала давайте вспомним распределительное свойство умножения относительно сложения и относительно вычитания и запишем их в буквенном виде.
Итак, распределительное свойство умножения относительно сложения гласит, что для того чтобы умножить сумму на число, можно умножить на это число
каждое слагаемое и сложить получившиеся произведения.
Распределительное свойство умножения относительно вычитания говорит, что
для того чтобы умножить разность на число, можно умножить на это число
уменьшаемое и вычитаемое и из первого произведения вычесть второе.
Также мы с вами знаем, что с помощью распределительного свойства очень удобно упрощать выражения. А ещё мы помним, что распределительное свойство позволяет раскрывать скобки и выносить общий множитель за скобки.
Итак, мы вооружились знаниями распределительного свойства умножения, а значит, теперь можем приступить к изучению новой темы.
Муравей за одну минуту пробегает 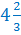
Но смотрите, эту задачу можно решить проще. Мы помним, что смешанное число это сумма целой и дробной части, значит, смешанное число можно записать в виде суммы. Что мы сейчас и сделаем.
Мы применили распределительное свойство умножения относительно сложения и упростили себе вычисления.
Чтобы умножить смешанное число на натуральное число, можно:
1) умножить целую часть на натуральное число;
2) умножить дробную часть на это натуральное число;
Помните, что всегда надо смотреть, как удобнее выполнять вычисления!
Правило умножения смешанных чисел:
Для того чтобы умножить смешанное число на смешанное число, можно:
1) перевести одно смешанное число в неправильную дробь;
2) умножить целую часть второго множителя на неправильную дробь;
3) умножить дробную часть второго множителя на неправильную дробь;
Найдите значение выражения:
Используя распределительное свойство умножения можно упрощать и буквенные выражения.
Итак, сегодня на уроке мы с помощью распределительного свойства умножения вывели правила умножения смешанных чисел.
Свойства умножения и деления
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Свойства умножения
Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.
Узнаем, какие бывают свойства умножения и как их применять.
Переместительное свойство умножения
От перестановки мест множителей произведение не меняется.
То есть, для любых чисел a и b верно равенство: a * b = b * a.
Это свойство можно применять к произведениям, в которых больше двух множителей.
Сочетательное свойство умножения
Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.
То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).
Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.
Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.
То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.
Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.
В обратную сторону распределительное свойство умножения относительно сложения звучит так:
Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.
То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.
В обратную сторону распределительное свойство умножения относительно вычитания звучит так:
Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.
Свойство единицы при умножении
Если умножить любое целое число на единицу, то в результате получится это же число.
То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.
Свойства деления
Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.
Основные свойства деления целых чисел
И еще одно важное свойство деления, которое проходят в 5 классе:
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.
Применим свойства деления на практике.
Пример 1
Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?
Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.
Пример 2
Вычислить: 500 * (100 : 5).
Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.
Ответ: 500 * (100 : 5) = 10000.
Пример 3
Упростить выражение: 27a – 16a.
Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.