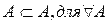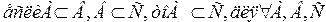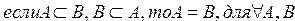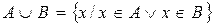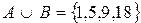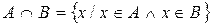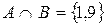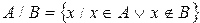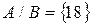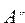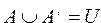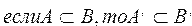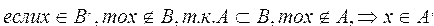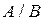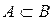Что значит пустое множество

Пустое множество

Пусто́е мно́жество (в математике) — множество, не содержащее ни одного элемента. Из аксиомы объёмности следует, что есть только одно множество, обладающее таким свойством. Пустое множество является своим (тривиальным) подмножеством, но не является своим элементом.

Пустое множество является конечным множеством и имеет наименьшую мощность среди всех множеств. Пустое множество — единственное множество, для которого класс множеств, равномощных ему, состоит из единственного элемента (самого́ пустого множества). Также, пустое множество — единственное множество, имеющее ровно 1 подмножество (само себя), и единственное множество, равномощное любому своему подмножеству.

Пустое множество тривиальным образом является разрешимым (а значит, перечислимым и арифметическим), транзитивным (англ.) и вполне упорядоченным множеством (для любого отношения порядка). Пустое множество является наименьшим порядковым числом и наименьшим кардинальным числом. В топологии, пустое множество является одновременно замкнутым и открытым множеством.

-цепочка, начинающаяся с произвольного множества, каждый последующий член которой является элементом предыдущего, всегда через конечное число шагов завершается пустым множеством (см. аксиому регулярности). Таким образом, пустое множество является «строительным кирпичиком», из которого строятся все остальные множества.

В некоторых формулировках теории множеств существование пустого множества постулируется (см. аксиому пустого множества), в других — доказывается.

Содержание

Обозначения пустого множества

Обычно пустое множество обозначают одним из следующих символов: , и .

Реже пустое множество обозначают одним из следующих символов: и .

В Юникоде имеется специальный символ «пустое множество» (U+2205, ∅ ).

Символы и введены в употребление группой Бурбаки (в частности, Андре Вейлем) в 1939 году.

Свойства пустого множества

См. также

Ссылки

Полезное

Смотреть что такое «Пустое множество» в других словарях:

пустое множество — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN empty set … Справочник технического переводчика

пустое множество — понятие теории множеств; пустое множество множество, не содержащее ни одного элемента; обозначается ø или 0. Понятие пустое множество (подобно понятию «нуль») возникает из потребности, чтобы результат всякой операции над множествами был также… … Энциклопедический словарь

пустое множество — tuščioji aibė statusas T sritis automatika atitikmenys: angl. empty set vok. Leerensemble, n rus. пустое множество, n pranc. ensemble vide, m … Automatikos terminų žodynas

Пустое множество — (математическое) «множество», не содержащее ни одного элемента. Понятие «П. м.» (подобно понятию «нуль»; возникает из потребности, чтобы результат всякой операции над множествами был также множеством (см. Множеств теория). Источником… … Большая советская энциклопедия

ПУСТОЕ МНОЖЕСТВО — понятие теории множеств; П. м. множество, не содержащее ни одного элемента; обозначается 0. Понятие П. м. (подобно понятию нуль ) возникает из потребности, чтобы результат всякой операции над множествами был также множеством … Естествознание. Энциклопедический словарь

Множество — У этого термина существуют и другие значения, см. Множество (значения). Запрос «Целое» перенаправляется сюда; о типе данных в программировании см. Целое (тип данных). Множество одно из ключевых понятий математики, в частности, теории… … Википедия

Множество (тип данных) — У этого термина существуют и другие значения, см. Множество (значения). Множество тип и структура данных в информатике, является реализацией математического объекта множество. Данные типа множество позволяют хранить ограниченное число значений… … Википедия

Множество (математика) — Множество один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном… … Википедия

Источник

Множество и его элементы. подмножество. пустое множество.

Понятие множества – одно из основных понятий математики. Под множеством понимают совокупность объектов (предметов или понятий), которая рассматривается как единое целое. Например, можно говорить о множестве натуральных чисел, о множестве букв на данной странице, о множестве корней данного уравнения и т. п. Понятие множества принимается как исходное, первичное, т. е. несводимое к другим понятиям. Объекты, входящие в состав множества, называются его элементами. Обычно множества обозначаются большими печатными буквами английского алфавита, например, множество А; а его элементы маленькими прописными буквами, например, элемент а.

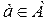
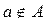
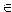
Запись означает, что элемент а принадлежит множеству А. Запись — наоборот, Что элемент а множеству А не принадлежит. Знак называют знаком принадлежности.

Определение 1. Два множества А и В называются равными и пишут А=В, если множества А и В содержат одни и те же элементы.

Например: <2, 4, 6>= <4, 2, 6>– равные множества.

Определение 2. Множество называется непустым, если содержит хотя бы один элемент.

Определение 3. Множество А является подмножеством множества В, если каждый элемент множества А принадлежит множеству В.

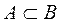
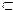
В этом случае пишут , знак называют знаком включения.

Например: <2, 4,>

Рассмотрим свойства отношения включения.

рефлексивно, т.е любое множество является подмножеством самому себе.

транзитивно, т. е. для любых множеств А, В и С, если множество А является подмножеством множества В и множество В является подмножеством множества С, то из этого следует, что множество А является подмножеством множества С.

антисимметрично, т. е. для любых множеств А и В следует, что, если множество А является подмножеством множества В и в то же время множество В является подмножеством множества А, то множества А и В равны.

Определение 4. Множество, не содержащее ни одного элемента, называется пустыммножеством.

Пустое множество обозначают

Пустое множество является подмножеством любого множества.

Определение 5. Множество всех подмножеств множества A называется множеством-степенью и обозначается P(A).

В дальнейшем будем пользоваться следующим утверждением:

Утверждение 1. Число всех подмножеств конечного множества равно 2n.

Пример. Выделим все подмножества множества А =<2, 4, 6>.

Р(А)=<2, 4, 6>, <2, 4>, <4, 6>, <2, 6>, <2>, <4 >, <6>, — всего 23=8.

Операции над множествами

Объединением множеств А и В называется множество, состоящее из тех элементов, которые принадлежат одному из множеств А или В.

Для обозначения объединения множеств используют знак .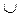

Пример. , ,

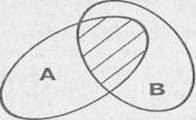
Пересечением множеств А и В называются такое множество, элементы которого принадлежат как множеству А, так и множеству В.

Для обозначения пересечения множеств используют знак .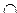

Пример. , ,

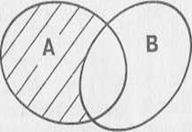
Разностью множеств А и В называется множество, элементы которого являются элементами множества А, не принадлежащие множеству В.

Для обозначения разности множеств используют знак /.

Пример. , ,

Перечислим основные свойства операций над множествами:

1) идемпотентность объединения

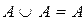
2) идемпотентность пересечения

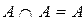
3) коммутативность объединения

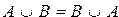
4) коммутативность пересечения

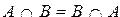
5) ассоциативность объединения

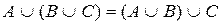
6) ассоциативность пересечения

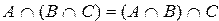
7) дистрибутивность объединения относительно пересечения

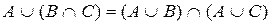
8) дистрибутивность пересечения относительно объединения

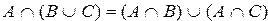
Универсальное множество. Дополнение множества.

Во многих приложениях теории множеств рассматриваются только такие множества, которые содержатся в некотором фиксированном множестве. Например, в геометрии мы имеем дело с множеством точек данного пространства, в арифметике – с множеством целых чисел. Такое фиксированное множество называют универсальным.Для его обозначения используют букву U.

Определение 6. Множество U/А называется дополнением множества А и обозначается (или ).

Дополнение U/ множества обозначается

Справедливы следующие формулы:

=

— закон инволюции.

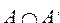
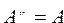
Теорема. Если множество А является подмножеством множества В, то дополнение множества А будет являться подмножеством дополнения множества В.

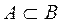
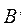
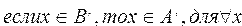
Пусть множество А является подмножеством множества В, , необходимо доказать, что для каждого элемента х из универсального множества U выполняется следующее условие: если элемент х принадлежит множеству , то он принадлежит и множеству .

.

Действительно, если х принадлежит множеству , то он не принадлежит множеству В, а т. к. множество А является подмножеством множества В, то элемент х не принадлежит и множеству А, а это означает его принадлежность множеству .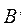

Теорема. Имеют место следующие тождества

— Законы де Моргана для множеств

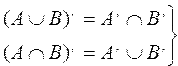
Приведем краткое доказательство первого утверждения.

Второе утверждение докажите самостоятельно.

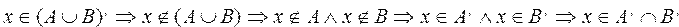
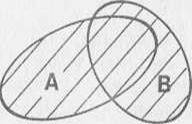
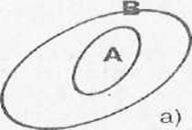
Для графического изображения множеств и их свойств используются так называемые диаграммы Эйлера-Венна.

Объединение множеств Пересечение множеств

Разность множеств Подмножество

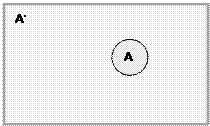
Универсальное множество Дополнение

Понятие множества. Элементы множества. Пустое множество. Принадлежность элементов.

Источник

О пустом множестве

Последняя загрузка: 09.05.2021

Содержание

О пустом множестве

Точки зрения

Часто в математической литературе «легко» доказывается, что пустое множество

является подмножеством любого другого (пустого или непустого) множества.

Основой такого доказательства служат приводимые ниже определения
подмножества и пустого множества (курсив и полужирный шрифт везде мои):

1. Множество А называется подмножеством множества В, если все элементы,

2. Множество, не содержащее ни одного элемента, называется пустым

и обозначается символом Ǿ (или обычным нулём: 0).

Совершенно очевидно, что в первом определении речь идёт о двух непустых

множествах, поскольку в каждом предполагается наличие элементов, которые

и сравниваются между собой.

Теперь посмотрим, как же на основании определения подмножества, которое

ЯВНО предполагает НАЛИЧИЕ элементов как во множестве, так и в его подмножестве,

доказывается, что пустое множество, определение которого ЯВНО предполагает

ОТСУТСТВИЕ элементов в нём, является подмножеством любого (пустого или

«… Пустое множество есть подмножество любого множества. Чтобы установить это,

надо доказать, что если А есть произвольное множество, то каждый элемент Ǿ

(вот именно: КАЖДЫЙ элемент Ǿ, а в Ǿ ИХ НЕТ! – Н.М.) есть элемент подмножества А.

Поскольку Ǿ не имеет элементов, то условие выполняется автоматически».

(Какая-то казуистика! – Н.М.)

Итак, «доказали»: каждый элемент Ǿ есть элемент А! Ну и ну! Так, чего доброго,

можно доказать и противоположное: Ǿ не является подмножеством А,

поскольку Ǿ не содержит элементов! Или ещё интереснее: поскольку А не содержит

ни одного элемента из Ǿ. Каково! Попробуй, опровергни!

Тем самым всякий элемент пустого множества содержится в любом множестве М.

А значит, любое множество М содержит пустое подмножество».

Голова моя явно слаба понять это. Ведь можно сказать и так:

Тем самым ни какой элемент пустого множества не содержится ни в каком

множестве М. А значит, никакое множество М не может содержать в качестве
подмножества пустое множество».

Пожалуй, разум более приемлет второе утверждение, как более понятное; – «раз нет,

то и говорить нечего», чем утверждение – «хотя нет, но есть:» (не путать с «понятным»
определением – « хотя и нет, но можно говорить…»)

«… Заметим, между прочим, что из определения отношения А следует, что,

каково бы ни было подмножество А множества J

Таким образом, «доказательства» во всех рассмотренных случаях

аналогичны. Чувствуя неубедительность своих аргументов, некоторые авторы

приводят «косвенные» доказательства того, что Ǿ

«… Хотя такое рассуждение (смотрите выше – Н.М.) правильно, в нём имеется

нечто неудовлетворительное. Имеется и другое, косвенное доказательство,

которое может оказаться более удобным. Это может быть лишь в том случае,

не являющийся множества А. Но это невозможно, так как Ǿ не имеет элементов.

Нетрудно провести аналогичное по форме «доказательство» противоположного

факта: Ǿ не принадлежит А. Действительно. Допустим, что Ǿ не принадлежит А

ложно (т.е. Ǿ – истинно). Это может быть лишь в том случае, если

не является ложным, т.е. Ǿ не принадлежит А ».

«… Свойство 4) (см. выше – Н.М.) может показаться несколько парадоксальным,

но если вдуматься (я очень пытался, но оказался слабоват – Н,М,), оно логически

строго соответствует точному смыслу определения знака

В самом деле, соотношение Ǿ нарушалось бы только в том случае,

если бы пустое множество Ǿ содержало элемент(да нету их там вообще. – Н.М.),

который не содержался бы в А, но так как пустое множество не содержит вовсе

элементов, то этого быть не может, каково бы ни было А».

А вот аналогичное по форме, но противоположное по результатам доказательство;

соотношение Ǿ не принадлежит А нарушалось бы только в том случае, если бы

множество А содержало бы все элементы … и т.д. и т.п. ( смотрите ранее
приведённое «контрдоказательство»).

Итак, любое доказательство утверждения Ǿ

На мой взгляд дать определение подмножества так, чтобы соотношение Ǿ

являлось его следствием, НЕЛЬЗЯ! Дело в том, что пустое множество

КАЧЕСТВЕННО отличается от непустого именно тем, что оно не содержит элементов.

Т. е. их вообще нелогично сравнивать!

Да, трудно доказать ЧТО-ТО, когда в разряд ЧЕГО-ТО зачисляется НИЧТО.

А поэтому удобное и необходимое для нас соотношение Ǿ нужно просто

ПОСТУЛИРОВАТЬ. Я так думаю.

«… Если, как это уже предполагалось выше, ввести в рассмотрение так

называемое пустое множество, т. е. множество, не содержащее ни одного

Некоторые авторы (см. например [5], стр. 14) фактически так и поступают.

Не исключено, однако, что здесь имеет место отказ от доказательства соотношения

Ǿ ввиду его «очевидности»

«… Если, как это уже предполагалось выше, ввести в рассмотрение так

называемое пустое множество, т. е. множество, не содержащее ни одного

Новая редакцЫя 17.03.2013 9:26

Литература:

[1], Множества. Логика. Аксиоматические теории,

[3], Что такое математика?

[5], Элементы теории функций и функционального анализа

Интересно сравнить

В некоторых формулировках теории множеств существование
пустого множества постулируется (см. аксиому пустого множества),
в других — доказывается.

Тема: «Около «науки»

Страницы : 23, 24, 40, 41, 77, 78, 79.

Источник