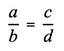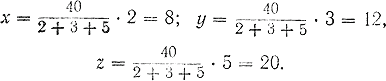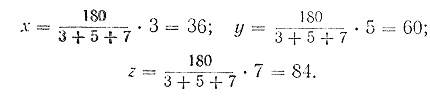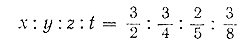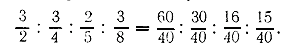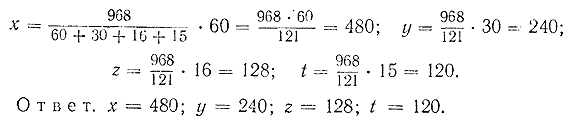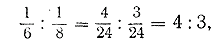Что значит пропорционально разделить
Пропорциональное деление
Пропорциональное деление — деление какой-нибудь величины на части, прямо или обратно пропорциональные данным числам.
Чтобы разделить число на части пропорционально нескольким данным числам, надо разделить его на сумму этих чисел и частное умножить на каждое из них.
Деление числа на пропорциональные части
Пример 1. Разделить число 50 на части пропорционально числам 2 и 3.
Решение: Надо найти такие два слагаемых числа 50, которые будут относиться друг к другу так, как 2:3. Первое слагаемое должно содержать 2 части числа, а второе 3, значит, число 50 содержит 5 таких частей (2 + 3 = 5), следовательно, каждая такая часть будет равна:
Число 10 — одна часть. Теперь надо умножить эту часть на числа, пропорционально которым требовалось разделить число 50:
Пример 2. Разделить число 90 на три слагаемых пропорционально числам 1, 2 и 3.
90 : (1 + 2 + 3) = 90 : 6 = 15;
Длинные отношения вида 1:2:3 называются сложными. Сложные отношения — это условные записи, показывающие, сколько долей содержит каждая часть. Если члены сложного отношения дробные, то, приведя их к общему знаменателю и умножив на него, можно заменить отношение дробных чисел отношением целых.
Пример. Разделить число 66 на такие три части, чтобы первая относилась ко второй, как 3:2, а вторая к третьей, как 5:4.
Первый способ: обозначим искомые части буквами a, b и c. Так как отношение не изменится, если оба члена умножить на одно и то же число, то умножим члены первого отношения на 5, а второго на 2:
значит a:b:c = 15:10:8. Так как 15 + 10 + 8 = 33, то
Второй способ: обозначим искомые части буквами a, b и c:
Если первая часть a равна 3, вторая b равна 2, то третью часть c можно определить из пропорции:
Следовательно, c равно:
Умножив все члены полученного сложного отношения на 5, чтобы избавиться от дробного члена, получим:
так как 15 + 10 + 8 = 33, то
Деление на части, обратно пропорциональные числам
Пример. Разделить число 62 на три части обратно пропорционально числам 2, 3 и 5, то есть разложить на три части, которые относились бы между собой, как
Решение: Обозначим искомые части буквами a, b и c. Приведём члены отношения к общему знаменателю и заменим дробные члены на целые числа:
Пропорциональное деление
Пропорциональное деление деление какой-нибудь величины на части, прямо или обратно пропорциональные данным числам.
Чтобы разделить число на части пропорционально нескольким данным числам, надо разделить его на сумму этих чисел и частное умножить на каждое из них.
Деление числа на пропорциональные части
Пример 1. Разделить число 50 на части пропорционально числам 2 и 3.
Решение: Надо найти такие два слагаемых числа 50, которые будут относиться друг к другу так, как 2:3. Первое слагаемое должно содержать 2 части числа, а второе 3, значит, число 50 содержит 5 таких частей (2 + 3 = 5), следовательно, каждая такая часть будет равна:
Число 10 одна часть. Теперь надо умножить эту часть на числа, пропорционально которым требовалось разделить число 50:
Пример 2. Разделить число 90 на три слагаемых пропорционально числам 1, 2 и 3.
90 : (1 + 2 + 3) = 90 : 6 = 15,
Длинные отношения вида 1:2:3 называются сложными. Сложные отношения это условные записи, показывающие, сколько долей содержит каждая часть. Если члены сложного отношения дробные, то, приведя их к общему знаменателю и умножив на него, можно заменить отношение дробных чисел отношением целых.
Пример. Разделить число 66 на такие три части, чтобы первая относилась ко второй, как 3:2, а вторая к третьей, как 5:4.
Первый способ: обозначим искомые части буквами a, b и c. Так как отношение не изменится, если оба члена умножить на одно и то же число, то умножим члены первого отношения на 5, а второго на 2:
значит a:b:c = 15:10:8. Так как 15 + 10 + 8 = 33, то
a = (66 : 33) ·, 15 = 30,
b = (66 : 33) ·, 10 = 20,
c = (66 : 33) ·, 8 = 16.
Второй способ: обозначим искомые части буквами a, b и c:
Если первая часть a равна 3, вторая b равна 2, то третью часть c можно определить из пропорции:
Следовательно, c равно:
| c = | 2 ·, 4 | = | 8 | , |
| 5 | 5 |
Умножив все члены полученного сложного отношения на 5, чтобы избавиться от дробного члена, получим:
так как 15 + 10 + 8 = 33, то
a = (66 : 33) ·, 15 = 30,
b = (66 : 33) ·, 10 = 20,
c = (66 : 33) ·, 8 = 16.
Деление на части, обратно пропорциональные числам
Пример. Разделить число 62 на три части обратно пропорционально числам 2, 3 и 5, то есть разложить на три части, которые относились бы между собой, как
Решение: Обозначим искомые части буквами a, b и c. Приведём члены отношения к общему знаменателю и заменим дробные члены на целые числа:
Задачи на пропорции
5 класс, 7 класс, 8 класс
Понятие пропорции
Чтобы решать задачи на тему пропорции, вспомним главное определение.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин.
Главное свойство пропорции:
Произведение крайних членов равно произведению средних.
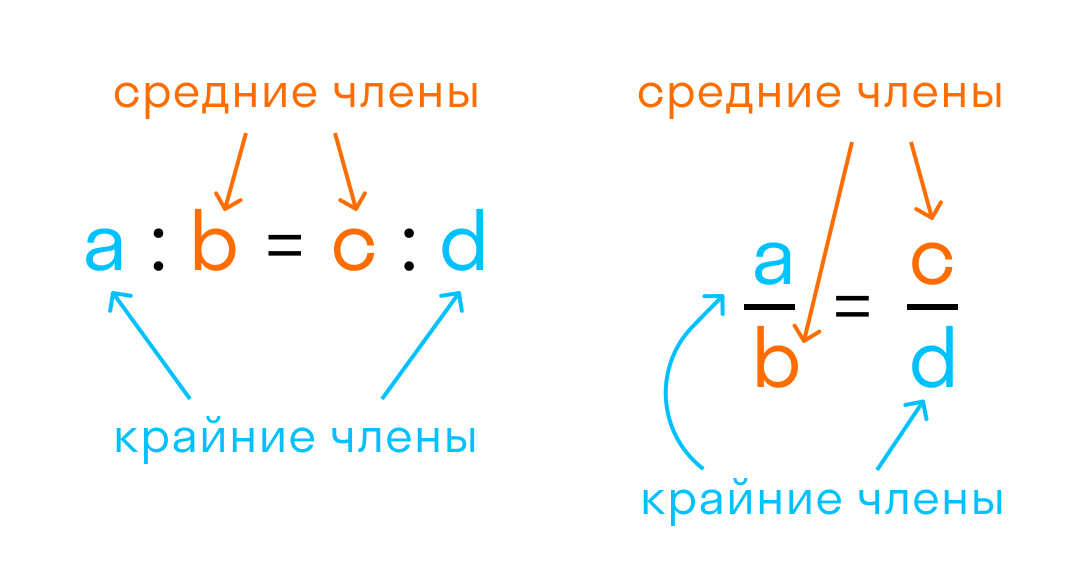
где a, b, c, d — члены пропорции, a, d — крайние члены, b, c — средние члены.
Вывод из главного свойства пропорции:
Решить пропорцию — значит найти неизвестный член. Свойство пропорции — главный помощник в решении.
Рассмотрим легкие и сложные задачи, которые можно решить с помощью пропорции. 5, 6, 7, 8 класс — неважно, всем школьникам полезно проанализировать занимательные задачки.
Задачи на пропорции с решением и ответами
Свойства пропорции придумали не просто так! С их помощью можно найти любой из членов пропорции, если он неизвестен. Решим 10 задач на пропорцию.
Задание 1. Найти неизвестный член пропорции: x/2 = 3/1
В этом примере неизвестен крайний член, поэтому умножим средние члены и разделим полученный результат на известный крайний член:
Задание 2. Найти неизвестный член: 1/3 = 5/y
Задача 3. Решить пропорцию: 30/x = 5/8
Задание 4. Решить: 7/5 = y/10
Задание 5. Известно, что 21x = 14y. Найти отношение x — к y
На следующем примере мы узнаем как составить пропорцию по задаче💡
Задание 6. Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?
Ответ: 36% всех подписчиков поставили лайк под постом.
Задание 7. Подруга Гарри Поттера при варке оборотного зелья использовала водоросли и пиявки в отношении 5 к 2. Сколько нужно водорослей, если есть только 450 грамм пиявок?
Ответ: на 450 грамм пиявок нужно взять 1125 гр водорослей.
Задание 8. Известно, что арбуз состоит на 98% из воды. Сколько воды в 5 кг арбуза?
Вес арбуза (5 кг) составляет 100%. Вода — 98% или х кг.
Ответ: в 5 кг арбуза содержится 4,9 кг воды.
Перейдем к примерам посложнее. Рассмотрим задачу на пропорции из учебника по алгебре за 8 класс.
Задание 9. Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Соотношения равны, но перевернуты относительно друг друга.
t2 = (75 * 13)/52 = 75/4 = 18 3/4 = 18 ч 45 мин
Ответ: 18 часов 45 минут.
Задание 10. 24 человека за 5 дней раскрутили канал в телеграм. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.
3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:
Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.
Что значит пропорционально разделить
ПРОПОРЦИИ И ПРОПОРЦИОНАЛЬНОСТЬ ВЕЛИЧИН
Глава двадцать первая.
§ 138. Деление числа на части прямо пропорционально данным числам.
Задача. В саду на двух участках посажено 224 штуки рассады клубники. Определить, сколько штук рассады посажено на каждом участке, если площадь первого участка 8 кв. м, а площадь второго 24 кв. м. (На каждом квадратном метре земли сажают рассаду в среднем поровну.)
Будем решать эту задачу так. Сначала определим площадь двух участков вместе:
Итак, площадь двух участков вместе 32 кв. м. Определим теперь, сколько штук рассады приходится на 1 кв. м:
Зная сколько рассады приходится на 1 кв. м, мы легко вычислим число штук рассады на 8 кв. м и на 24 кв.. м, т. е. ответим на вопрос задачи:
Подумаем теперь, какие величины входят в нашу задачу и как они связаны между собой. В условие задачи входят две величины: 1) количество штук рассады, 2) площадь участка. Эти две величины прямо пропорциональны одна другой, потому что, чем больше площадь участка, тем больше на нём можно посадить рассады. Расположим числа, с которыми мы имели дело в задаче, так, чтобы их удобно было сравнивать:
8 кв. м — 56 штук
24 кв. м — 168 штук
Из этой таблички видно, что второй участок втрое больше первого и рассады на нём в три раза больше, чем на первом.
Итак, в этой задаче мы разделили число штук рассады пропорционально площадям двух участков. Это и есть одна из возможных задач на пропорциональное деление. Как же решаются такие задачи? В задаче требовалось число 224 разделить на две части, пропорциональные числам 8 и 24, т. е. разделить это число на такие две части, которые относились бы между собой так же, как 8 : 24. Обозначим величину первой части буквой х, а второй части — у и напишем отношение этих частей:
Для нахождения этих частей были выполнены следующие действия. Число 224 разделили на сумму чисел 8 и 24 и затем найденное частное последовательно умножили сначала на 8, а потом на 24, т. е.
Словами эти равенства можно высказать так: чтобы разделить некоторое число на части пропорционально данным числам, надо разделить его на сумму этих чисел и полученное частное последовательно умножить на каждое из этих чисел.
Рассмотрим другую задачу: «За три куска мыла одного и того же сорта заплатили 40 руб, Сколько заплатили за каждый из них, если первый кусок весил 2 кг, второй 3 кг и третий 5 кг?»
В этой задаче требуется разделить 40 руб. на 3 части пропорционально весу отдельных кусков мыла. Обозначим стоимость первого куска буквой х, второго куска — у и третьего — z.
Воспользуемся правилом, выведенным при решении первой задачи. Согласно этому правилу для нахождения искомых чисел необходимо число, подлежащее делению, разделить на сумму данных чисел и полученное частное умножить последовательно на каждое из них. Следовательно:
Таким образом, первый кусок мыла стоит 8 руб., второй 12 руб. и третий 20 руб. Найденные числа рублей х, у, z находятся между собой в таких же отношениях, как и данные в задаче числа весовых единиц, т. е.
х : у : z = 8 : 12 : 20 = 2 : 3 : 5.
Рассмотрим теперь задачу с отвлечёнными числами. Разделить число 180 на три части пропорционально числам 3; 5; 7. Иными словами: в этой задаче требуется разложить число 180 на такие три слагаемых, чтобы первое относилось ко второму, как 3 к 5, второе относилось к третьему, как 5 к 7 и, наконец, первое к третьему, как 3 к 7. Сокращённо это можно написать так:
где х, у, z обозначают соответственно первое, второе и третье число.
Содержание этой задачи можно пояснить ещё так: требуется разложить число 180 на 3 числа так, чтобы первое число содержало три части (три доли, три пая), второе — пять таких же частей и третье — семь таких же частей.
Применяя указанное выше правило, можем написать:
Полученные три числа удовлетворяют условию задачи: они в сумме составляют 180, т. е.
36 + 60 + 84 = 180 и 3 : 5 : 7 = 36 : 60 : 84.
Мы решили три задачи на пропорциональное деление. Покажем теперь другие способы решения таких задач.
Задача 1. Определить квартирную плату за каждую из двух комнат (8 кв. м и 24 кв. м), если за обе вместе нужно заплатить 64 руб.
Обозначим плату за 1 кв. м буквой х; тогда за первую комнату нужно будет заплатить 8x, а за вторую — 24x. Значит, за обе комнаты вместе надо заплатить 8х + 24х, что составляет 64 руб. Следовательно, можно записать равенство:
Дальше задача решается так:
Задача 2. Найти стоимость каждого из трёх пакетов муки, если все три пакета стоят 40 руб., а вес первого 2 кг, второго 3 кг и третьего 5 кг.
Обозначим цену одного килограмма буквой х, тогда:
2 кг будут стоить 2х ;
а вся мука будет стоить:
После этого легко определить стоимость каждого пакета;
Задача 3. Разделить число 1 800 на три слагаемых пропорционально числам: 3, 5 и 7.
Рассуждаем так: в первом слагаемом 3 части, во втором 5 и в третьем 7.
Обозначая величину одной части буквой х, можно написать:
15х = 1 800; х = 1 800 : 15 = 120.
Решим теперь задачу, в которой «некоторое число придётся разделить на четыре части пропорционально дробным числам.
а сумма x + y + z + t = 968.
Заменим отношения дробных чисел отношениями целых чисел, для чего приведём эти дроби к общему знаменателю:
Отбрасывая общий знаменатель 40, получим: 60 : 30 : 16 : 15. Вычислим последовательно каждое из искомых чисел:
§ 139. Деление числа на части обратно пропорционально данным числам.
Теперь перейдём к решению задач, в которых придётся некоторое число делить обратно пропорционально данным числам.
Задача. В двух полевых бригадах 70 колхозников. Каждой бригаде поручено обработать одинаковые участки. Сколько колхозников в каждой бригаде, если первая бригада выполнила работу в 6 дней, а вторая — в 8 дней? (Предполагается, что все колхозники работают с одинаковой производительностью труда.)
Очевидно, мы не имеем права делить число колхозников на две части пропорционально времени, которое каждая бригада употребила на работу, так как та бригада, которая быстрее окончила свою работу, была, по-видимому, более многочисленная, чем другая. Поэтому решать эту задачу так же, как мы решали предыдущие задачи, нельзя.
Будем рассуждать следующим образом. Первая бригада колхозников окончила свою работу в 6 дней; значит, в один день она выполняла 1 /6 часть всей работы; вторая бригада окончила такую же работу в 8 дней, значит в один день она выполняла 1 /8 всей работы.
т. е. число 70 нужно разделить на две части пропорционально числам 4 и 3. Обозначим число колхозников первой бригады буквой х, а второй — буквой у и вычислим:
Для решения задачи требуется разделить 70 рабочих на две неравные бригады, исходя из количества времени (дней), затраченного ими на работу. Это время выражается числами 6 (дней) и 8 (дней). Вместо этих двух чисел мы берём обратные им числа 1 /6 и 1 /8 и пропорционально им делим число 70.
Такая замена сделана нами потому, что число работников не прямо, а обратно пропорционально времени, затраченному на работу. О такой задаче принято говорить, что в ней число 70 разделено на две части обратно пропорционально числам 6 и 8, т. е. в ней первая часть относится ко второй не как 6 к 8, а как 8 к 6.
Итак, чтобы разделить число на части обратно пропорционально данным числам, нужно это число разделить прямо пропорционально обратным числам.
Задача. Разделить 65 на три части обратно пропорционально числам: 2, 3, 4.
Мы теперь знаем, что разделить число на части обратно пропорционально нескольким числам — это значит разделить его на столько же частей прямо пропорционально обратным числам.
Напишем числа, обратные данным в задаче:
данные числа 2, 3, 4;
Пропорционально этим последним и нужно разделить число 65. Приведём дроби к общему знаменателю:
а потом освободимся от него:
Значит, число 65 нужно разделить на три части пропорционально числам 6 : 4 : 3.
Обозначим первую часть буквой х, вторую часть буквой у, третью часть буквой z. Тогда
Пропорциональное распределение доли общества при выходе участника из ООО
Инструкция по пропорциональному распределению доли
Распределение доли после выхода участника Общества
Законом установлено, что в течение одного года со дня перехода доли или части доли в Уставном капитале к Обществу они должны быть по решению общего собрания участников Общества распределены между всеми участниками Общества пропорционально их долям в Уставном капитале Общества или предложены для приобретения всем, либо некоторым участникам Общества.
В первом случае мы говорим о пропорционально распределении доли общества. Во втором случае имеется ввиду именно непропорциональное распределение. В этом случае между обществом в лице его руководителя и покупателем заключается договор купли-продажи.
Когда происходит пропорциональное распределение
В случае наличия у участников желания оставить прежним соотношения своих долей в уставном капитале, они принимают решение о пропорциональном распределении доли общества. Также необходимо, чтобы при расчете распределения доли была возможность математически верно рассчитать новое процентное соотношение долей.
Правильное пропорциональное распределение
Рассмотрим, как правильно распределить доли между участниками ООО при выходе одного или нескольких участников на примере:
В составе ООО три участника с нижеуказанными долями. Для удобства определим участникам ООО порядковые номера: 1, 2, 3. Размер уставного капитала – 10 000 рублей.
Из состава выходит участник №3. Задача: определить доли оставшихся участников после его выхода.
1 – 45% или 4 500 рублей или 45/100
2 – 30% или 3 000 рублей или 30/100
3 – 25% или 2 500 рублей или 25/100
Поскольку выходит участник №3 с долей 25% или 2 500 рублей, то нам необходимо распределить его долю среди оставшихся участников пропорционально их долям в уставном капитале ООО.
Для этого нам нужно, определить долю, принадлежащую ООО — 2 500 рублей или 25% или 25/100.
Определяем сумму долей, принадлежащих оставшимся участникам:
Доля участника №1 + доля участника №2 = 45% + 30% = 75%
В том числе доля участника №1 = 45/75
В том числе доля участника №2 = 30/75
Далее необходимо долю, принадлежащую ООО (2 500 рублей) умножить на вышеуказанные доли участников:
Участник №1 = 2 500 * 45/75 = 1 500 рублей
Участник №2 = 2 500 * 30/75 = 1 000 рублей
Т.е., из доли, принадлежащей ООО, участнику №1 переходит 1 500 рублей, а участнику №2 – 1 000 рублей.
Таким образом, после распределения доли ООО доли оставшихся участников увеличиваются не только в денежной выражении, но и в процентном:
Участник №1 = 4 500 + 1 500 = 6 000 рублей
Участник №2 = 3 000 + 1 000 = 4 000 рублей
Процентное выражение долей станет следующим (для этого необходимо денежное выражение доли участника поделить на общий размер уставного капитала и умножить на 100):
Участник №1 = 6 000 / 10 000 * 100 = 60%
Участник №2 = 4 000 / 10 000 * 100 = 40%
Также существует более простая формула для распределения доли принадлежащей Обществу между остальными участниками пропорционально.
Новая доля участника = сумма уставного капитала / (разделить на) суммарную долю в процентах остающихся участников х (умножить на) долю конкретного участника до распределения доли.
Таким образом будет вычислена новая доля участника в денежном выражении. Чтобы рассчитать в процентах нужно эту сумму разделить на сумму всего уставного капитала и умножить на 100.
Необходимые документы
Чтобы уведомить налоговую о факте пропорционального распределения доли одновременно с выходом участника потребуется следующий пакет документов:
Обратите внимание, что форма Р14001 с 25 ноября 2020 года больше не применяется. Новая форма Р13014 утверждена Приказом ФНС России от 31.08.2020 N ЕД-7-14/617@.