Что значит промежуточное число
Как найти промежуточное число при сравнении дробей. Сравнение обыкновенных дробей
В этом уроке мы научимся сравнивать дроби между собой. Это очень полезный навык, который необходим для решения целого класса более сложных задач.
Для начала напомню определение равенства дробей:
Во всех остальных случаях дроби являются неравными, и для них справедливо одно из следующих утверждений:
Конечно, в приведенных примерах с нулями был явный перебор, но смысл именно такой: заполнить недостающие разряды слева, а затем сравнить.
По определению имеем:
Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.
Сравнение дробей с одинаковыми знаменателями
Отсюда следует правило сравнения дробей с одинаковыми знаменателями:из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.
Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.
Сравнение дробей с разными знаменателями
Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.
Если имеются дроби с разными знаменателями, для их сравнения необходимо:
Рассмотрим данные действия на примере.
Сравнение дробей с одинаковыми числителями
Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.
Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.
Рассмотрим на примере.
Сравнение дроби с натуральным числом
И действительно, если вы съедите 3 куска пиццы, разделенной на 4 части, то будете более сыты, чем если бы съели 3 куска пиццы, разделенной на 8 частей.
Сравнение дробей с разными числителями и знаменателями
Применяем третье правило:
Сравнение дробей с разными знаменателями нужно привести к сравнению дробей с одинаковыми знаменателями. Для этого необходимо привести дроби к общему знаменателю и использовать первое правило.
Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.
Сравнение дробей с одинаковыми знаменателями.
Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.
Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.
Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:
Если мы до решаем эти дроби, то получим числа \(\frac<20> <4>= 5\) и \(\frac<20> <10>= 2\). Получаем, что 5 > 2
В этом и заключается правило сравнения дробей с одинаковыми числителями.
Рассмотрим еще пример.
Так как числители одинаковые, больше та дробь, где знаменатель меньше.
Пример №2:
Сравните правильную дробь с единицей?
Решение:
Любая правильная дробь всегда меньше 1.
Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?
Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби \(\frac<5> <10>\).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби \(\frac<3> <5>\).
Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.
Надеюсь, данное объяснение поможет Вам.
Например, можно записать, что 41 / 80 > ; 245 / 504, потому что первая дробь больше половины, а вторая – меньше.
Сравните числа используя прием сравнения с промежуточным числом 11 / 18 и 10 / 23?
Сравните числа используя прием сравнения с промежуточным числом 11 / 18 и 10 / 23.
Сравните числа, используя приём сравнения с» промежуточным » числом одиннадцать двенадцатых и десять двадцать третьих можно с решением плиз?
Сравните числа, используя приём сравнения с» промежуточным » числом одиннадцать двенадцатых и десять двадцать третьих можно с решением плиз.
Геометрическая прогрессия?
Как найти промежуточный ее член?
Ну, например я знаю b4 и b6, как найти b5?
Найти правильную дробь, большую 1 / 3, при увеличении числителя которой на некоторое натуральное число и умножении знаменателя на то же число значение дроби не изменяется ПОМОГИТЕ?
Найти правильную дробь, большую 1 / 3, при увеличении числителя которой на некоторое натуральное число и умножении знаменателя на то же число значение дроби не изменяется ПОМОГИТЕ!
Как сравнивать числа с промежуточным числом?
Как сравнивать числа с промежуточным числом?
И как его находить?
Сравнение обыкновенных дробей?
Сравнение обыкновенных дробей.
Сравните числа используя прием сравнения с промежуточным числом 5 / 28 и11 / 40, 29 / 15и25 / 12?
Сравните числа используя прием сравнения с промежуточным числом 5 / 28 и11 / 40, 29 / 15и25 / 12.
(Много баллов?
) Найти правильную дробь, не превышающую 1 / 3, зная, что от увеличения ее числителя на некоторое целое число и умножения знаменателя на то же число величина дроби не меняется.
Найти квадратный корень из числа 1 дробь 64?
Найти квадратный корень из числа 1 дробь 64.
Сравни числа найдя какое нибудь промежуточное число 60 / 26 и 38 / 12 желательно с объяснениями?
Сравни числа найдя какое нибудь промежуточное число 60 / 26 и 38 / 12 желательно с объяснениями.
Таблица числовых промежутков: виды, обозначения, изображения
Среди множеств чисел имеются множества, где объектами выступают числовые промежутки. При указывании множества проще определить по промежутку. Поэтому записываем множества решений, используя числовые промежутки.
Данная статья дает ответы на вопросы о числовых промежутках, названиях, обозначениях, изображениях промежутков на координатной прямой, соответствии неравенств. В заключение будет рассмотрена таблица промежутков.
Виды числовых промежутков
Каждый числовой промежуток характеризуется:
Числовой промежуток задается при помощи любых 3 способов из выше приведенного списка. То есть при использовании неравенства, обозначения, изображения на координатной прямой. Данный способ наиболее применимый.
Произведем описание числовых промежутков с выше указанными сторонами:
Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой и ее числами имеется соответствие, благодаря которому прямую называем координатной. Если необходимо сравнить числа, то на координатной прямой большее число находится правее. Тогда неравенство вида x a включает в себя точки, которые расположены левее, а для x > a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промежуток, который необходим, выделяют при помощи штриховки. Рассмотрим рисунк, приведенный ниже.
Рассмотрим несколько примеров.
Для наглядного примера зададим числовой луч.
Рассмотрим рисунок, приведенный ниже.
Таблица числовых промежутков
Промежутки могут быть изображены в виде:
Чтобы упростить процесс вычисления, необходимо пользоваться специальной таблицей, где имеются обозначения всех видов числовых промежутков прямой.
Что такое промежуточное число при сравнении дробей. Сравнение дробей. Как сравнивать дроби с разными знаменателями? Сравнение дроби с натуральным числом
Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.
Сравнение дробей с одинаковыми знаменателями.
Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.
Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.
Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:
Если мы до решаем эти дроби, то получим числа \(\frac<20> <4>= 5\) и \(\frac<20> <10>= 2\). Получаем, что 5 > 2
В этом и заключается правило сравнения дробей с одинаковыми числителями.
Рассмотрим еще пример.
Так как числители одинаковые, больше та дробь, где знаменатель меньше.
Пример №2:
Сравните правильную дробь с единицей?
Решение:
Любая правильная дробь всегда меньше 1.
Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?
Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби \(\frac<5> <10>\).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби \(\frac<3> <5>\).
Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.
Сравнение дробей с одинаковыми числителями
Дроби с одинаковыми числителями и разными знаменателями, несомненно, можно сравнивать с помощью правил, разобранных в предыдущем пункте. Однако, результат сравнения таких дробей легко получить, сравнив знаменатели этих дробей.
Существует такое правило сравнения дробей с одинаковыми числителями : из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель, и меньше та дробь, знаменатель которой больше.
Рассмотрим решение примера.
Начнем урок словами французского писателя А.Франса: “Учиться можно весело….Чтобы переварить знания, надо поглощать их с аппетитом”.
Последуем этому совету, постараемся быть внимательными, будем поглощать знания с большим желанием, т.к. они пригодятся нам в дальнейшем.
2. Актуализация знаний учащихся.
1.)Фронтальная устная работа учащихся.
Цель: повторить пройденный материал, требующийся при изучении нового:
А) правильные и неправильные дроби;
Б) приведение дробей к новому знаменателю;
В) нахождение наименьшего общего знаменателя;
(Проводится работа с файлами. Учащиеся имеют их в наличии на каждом уроке. На них пишут ответы фламастером, а за тем ненужная информация стирается.)
Задания для устной работы.
1. Назвать лишнюю дробь среди цепочки:
2. Привести дроби к новому знаменателю 30:
Найти наименьший общий знаменатель дробей:
1/5 и 2/7; 3/4 и 1/6; 2/9 и 1/2.
2.) Игровая ситуация.
Ребята, наш знакомый клоун (учащиеся познакомились с ним в начале учебного года) попросили меня помочь решить ему задачу. Но я считаю, что вы, ребята, сможете без меня помочь нашему другу. А задача следующая.
а) 1/2 и 1/6;
б) 3/5 и 1/3;
в) 5/6 и 1/6;
г) 12/7 и 4/7;
д) 3 1/7 и 3 1/5;
е) 7 5/6 и 3 1/2;
ж) 1/10 и 1;
з) 10/3 и 1;
и) 7/7 и 1.”
Ребята, чтобы помочь клоуну, чему мы должны научиться?
Цель урока, задачи (учащиеся формулируют самостоятельно).
Учитель помогает им, задавая вопросы:
а) а какие из пар дробей мы сможем уже сравнить?
б) какой инструмент для сравнения дробей нам необходим?
3. Ребята в группах (в постоянных разноуровневых).
Каждой группе выдается задание и инструкция к его выполнению.
Первая группа: Сравнить смешанные дроби:
и вывести правило равнения смешанных дробей с одинаковыми и с разными целыми частями.
Инструкция: Сравнение смешанных дробей (используется числовой луч)
Вторая группа: Сравнить дроби с разными знаменателями и разными числителями. (использовать числовой луч)
Третья группа: Сравнение дробей с единицей.
а)2/3 и 1;
б) 8/7 и 1;
в)10/10 и 1 и сформулировать правило.
Рассмотрите все случаи: (используйте числовой луч)
Четвертая группа: Сравните дроби:
а) 5/8 и 3/8;
б) 1/7 и 4/7 и сформулируйте правило сравнения дробей с одинаковым знаменателем.
Используйте числовой луч.
Сравните числители и сделайте вывод, начиная словами: “Из двух дробей с одинаковыми знаменателями……”.
Пятая группа: Сравните дроби:
а) 1/6 и 1/3;
б) 4/9 и 4/3, используя числовой луч:
Сформулируйте правило сравнения дробей с одинаковыми числителями.
Сравните знаменатели и сделайте вывод, начиная со слов:
“Из двух дробей с одинаковыми числителями………..”.
Шестая группа: Сравните дроби:
а) 4/3 и 5/6; б) 7/2 и 1/2, используя числовой луч
Сформулируйте правило сравнения правильных и неправильных дробей.
Подумайте, какая дробь всегда больше, правильная или неправильная.
4. Обсуждение выводов, сделанных в группах.
Слово каждой группе. Формулировка правил учащихся и сравнение их с эталонами соответствующих правил. Далее выдаются распечатки правила сравнения различных видов обыкновенных дробей каждому учащемуся.
5. Возвращаемся к задаче, поставленной в начале урока. (Решаем задачу клоуна вместе).
6. Работа в тетрадях. Используя правила сравнения дробей, учащиеся под руководством учителя сравнивают дроби:
а) 8/13 и 8/25;
б)11/42 и 3/42;
в)7/5 и 1/5;
г) 18/21и 7/3;
д) 2 1/2 и 3 1/5 ;
е) 5 1/2 и 5 4/3;
(возможно приглашение ученика к доске).
7. Учащимся предлагается выполнить тест по сравнению дробей на два варианта.
1) сравнить дроби: 1/8 и 1/12
1) сравнить дроби: 3/5 и 3/10
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем пиццы:
Сравнение дробей с одинаковыми числителями
Следующий случай, в который мы можем попасть, это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:
Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с разными числителями и разными знаменателями
Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями.
Приведём дроби и к одинаковому (общему) знаменателю. Найдём (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.
Умножим дроби на свои дополнительные множители:
Мы пришли к тому, что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
2 целые пиццы и пиццы, больше чем пиццы.
Вычитание смешанных чисел. Сложные случаи.
Вычитая смешанные числа, иногда можно обнаружить, что всё идёт не так гладко, как хотелось бы. Часто случается так, что при решении какого-нибудь примера ответ получается не таким, каким он должен быть.
При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.
Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.
А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5−7=−2
В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.
Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.
С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.
Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем
поэтому смело можем вернуться к примеру и решить его:
Теперь решим такой пример
Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:
В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.
Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:
После приведения дробей к одинаковому знаменателю, получаем следующее выражение:
А это значит, что уменьшаемое больше, чем вычитаемое
А значит мы можем вернуться к нашему примеру и смело решить его:
Пример 3. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:
Формула ПРОМЕЖУТОЧНЫЕ ИТОГИ — основные функции с примерами.
В статье объясняются особенности функции ПРОМЕЖУТОЧНЫЕ.ИТОГИ в Excel и показано, как использовать формулы промежуточных итогов для суммирования данных в видимых ячейках.
В предыдущей статье мы обсудили автоматический способ вставки промежуточных итогов в Excel с помощью инструмента Промежуточные итоги. Сегодня вы узнаете, как можно самостоятельно создавать формулы промежуточных итогов и какие преимущества это дает.
Синтаксис и использование.
Microsoft определяет ПРОМЕЖУТОЧНЫЕ.ИТОГИ как функцию, которая возвращает промежуточный итог в таблице данных. И это не просто суммирование чисел в определенном диапазоне ячеек.
В отличие от других функций Excel, которые предназначены только для одной конкретной задачи, она удивительно универсальна. Она может выполнять различные арифметические и логические операции, такие как подсчет количества значений, вычисление среднего, поиск минимального или максимального и многое другое.
Функция ПРОМЕЖУТОЧНЫЕ.ИТОГИ (на английском — SUBTOTAL) доступна во всех версиях Excel 2019, 2016 и ниже.
Синтаксис ее следующий:
ПРОМЕЖУТОЧНЫЕ.ИТОГИ(номер_функции; ссылка1; [ссылка2];…)
Аргумент номер_функции может принимать значения:
На самом деле нет необходимости запоминать все эти номера. Как только вы начнете вводить формулу промежуточного итога в ячейку или в строку формул, Microsoft Excel отобразит для вас список доступных функций с номерами. Останется только выбрать подходящую.
Например, вот как вы можете составить формулу с номером 9 для суммирования значений в ячейках с C2 по C8:
Чтобы добавить номер функции в формулу, дважды щелкните его в списке, затем поставьте точку с запятой, укажите диапазон, введите закрывающую скобку и нажмите Enter. Готовая формула будет выглядеть так:
Аналогичным образом вы можете написать формулу с 1 для получения среднего значения, с 2 для подсчета ячеек с числами, указать 3 для подсчета непустых значений и т. д. На скриншоте ниже показаны несколько других формул с различными функциями в действии:
Особенности формулы ПРОМЕЖУТОЧНЫЕ.ИТОГИ:
Существенное преимущество этой формулы в том, что ее можно использовать почти в любом месте вашего рабочего листа. То есть, таблица может не быть настолько жестко упорядоченной, как при использовании инструмента «Промежуточные итоги».
Теперь, когда вы знаете, как создать формулу промежуточных итогов в Excel, главный вопрос: зачем вообще тратить силы на ее изучение? Почему бы просто не использовать обычные функции, такие как СУММ, СЧЁТ, МАКС и т.д.? Вы найдете ответ ниже.
3 основных причины использовать ПРОМЕЖУТОЧНЫЙ ИТОГ в Excel
По сравнению с традиционными функциями Excel, ПРОМЕЖУТОЧНЫЕ.ИТОГИ дает следующие важные преимущества.
1. Вычисляет значения с учетом применяемого фильтра.
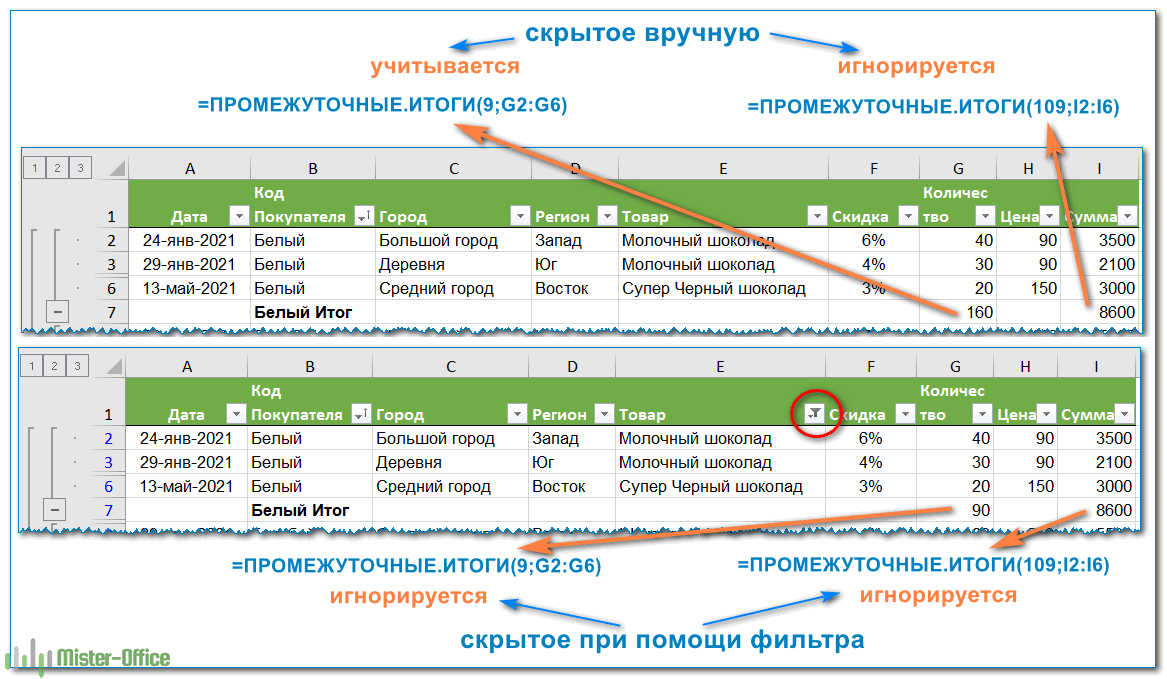
Поскольку функция Excel ПРОМЕЖУТОЧНЫЕ.ИТОГИ игнорирует значения в отфильтрованных строках, вы можете использовать ее для создания динамической сводки данных, в которой промежуточные итоги пересчитываются автоматически в соответствии с фильтром. Скрытые фильтром значения при этом учитываться не будут.
А вот если мы будет использовать обычную функцию, к примеру, СУММ, то применение фильтра не изменит вычисленный итог. Складываются в том числе и скрытые фильтром числа.
Например, если мы отфильтруем таблицу, чтобы отобразить продажи только черного шоколада, формула промежуточного итога не изменится, но все остальные товары будут удалены из итога:
Стандартная функция СУММ с подсчетом только нужных ячеек не справится. Придется либо копировать эти данные в другое место, чтобы все другие не мешали, либо применять функцию СУММЕСЛИ и постоянно корректировать ее в соответствии с нужными целями.
Примечание. Поскольку оба набора номеров функций (1-11 и 101-111) игнорируют отфильтрованные ячейки, в этом случае вы можете использовать формулу с функцией номер 9 или 109.
2. Вычисление только видимых ячеек.
Как вы помните, формулы промежуточных итогов с номером функции от 101 до 111 игнорируют все скрытые ячейки – отфильтрованные и скрытые вручную. Итак, когда вы используете функцию «Скрыть» в Excel для удаления из представления нерелевантных данных, используйте функцию номер 101-111, чтобы исключить значения в скрытых строках из подсчета итогов.
| Номер функции | Отфильтрованные значения | Скрытые вручную |
| 1-11 | игнорируются | учитываются |
| 101-111 | игнорируются | игнорируются |
На рисунке ниже вы видите, что не следует использовать функцию 9, если вы руками скрывали какие-либо строки в вашей таблице. При этом функция 109 всегда возвращает результат исходя только из видимых на экране значений.
Следующий пример поможет вам лучше понять, как это работает: Промежуточный итог 9 против 109.
3. Игнорируются значения во вложенных формулах промежуточных итогов.
Если диапазон, указанный в вашей формуле промежуточных итогов Excel, содержит любые другие формулы промежуточных итогов, эти вложенные итоги будут проигнорированы, поэтому одни и те же числа не будут вычисляться дважды. Ведь нам не нужен двойной счёт. Классно, не правда ли?
На снимке экрана ниже формула
игнорирует результаты формул промежуточных итогов в ячейках G7 и G120, как если бы вы использовали функцию СУММ с двумя отдельными диапазонами: СУММ(G2:C6, G8:G11).
Когда вы впервые сталкиваетесь с промежуточными итогами, это может показаться сложным, запутанным и даже не слишком нужным. Но как только вы узнаете все подробности, то поймете, что овладеть ими не так уж и сложно, а пользы может быть много. Следующие примеры дадут вам несколько полезных советов и новых идей.
Пример 1. Промежуточный итог с функцией 9 или 109?
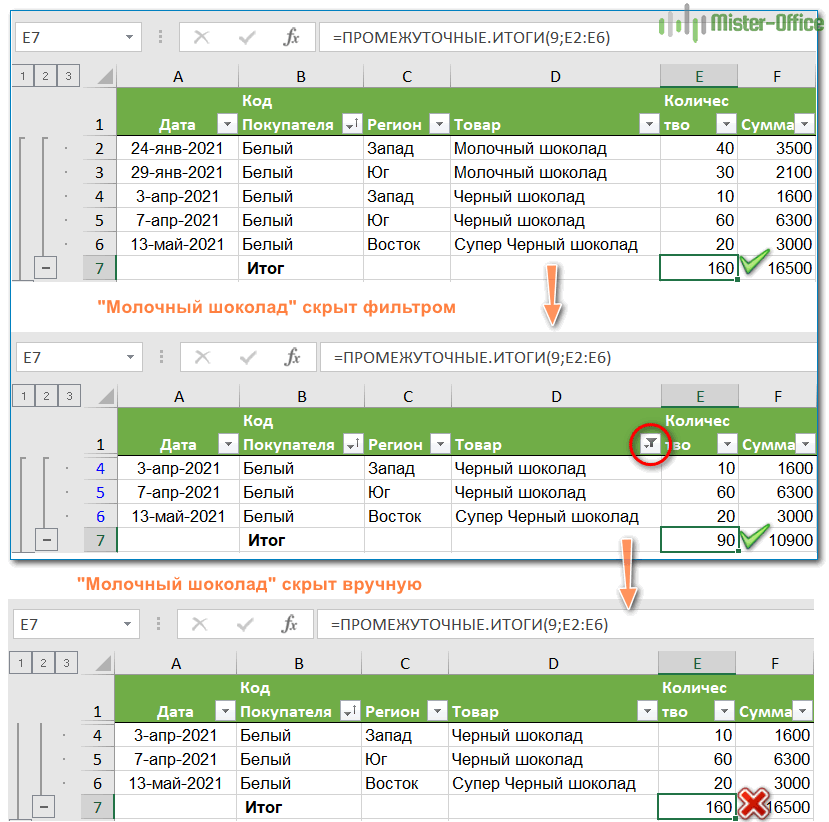
Как вы уже знаете, ПРОМЕЖУТОЧНЫЕ.ИТОГИ использует 2 набора номеров функций: 1-11 и 101-111. Все они игнорируют отфильтрованные строки, но номера 1–11 учитывают скрытые вручную строки, а номера 101–111 исключают их. Чтобы лучше понять разницу, давайте рассмотрим следующий пример.
Чтобы суммировать отфильтрованные строки, вы можете использовать формулу Промежуточный итог с функцией 9 или с 109, как показано на рисунке ниже:
Но если вы скрыли отдельные элементы вручную,
и теперь хотите суммировать значения только в видимых строках, использовать функцию 109 – это единственный вариант:
Остальные номера функций работают таким же образом. Например, для подсчета непустых отфильтрованных ячеек подойдет формула с функцией 3 или 103. Но только функция 103 может правильно подсчитывать видимые значения, если в диапазоне есть скрытые вручную строки.
Примечание. Функция Excel ПРОМЕЖУТОЧНЫЕ.ИТОГИ с номерами 101-111 игнорирует значения в скрытых строках, но не в скрытых столбцах. Например, если вы используете формулу =ПРОМЕЖУТОЧНЫЕ.ИТОГИ(109;D2:H10) для суммирования чисел в горизонтальном диапазоне (по строке), то скрытие столбца F не повлияет на результат.
Пример 2. Промежуточные итоги с условием.
Если вы создаете сводный отчет или информационную панель, где вам нужно отображать различные сводные данные, но у вас ограничено место, чтобы разместить множество вариантов итогов, то можно сделать так:
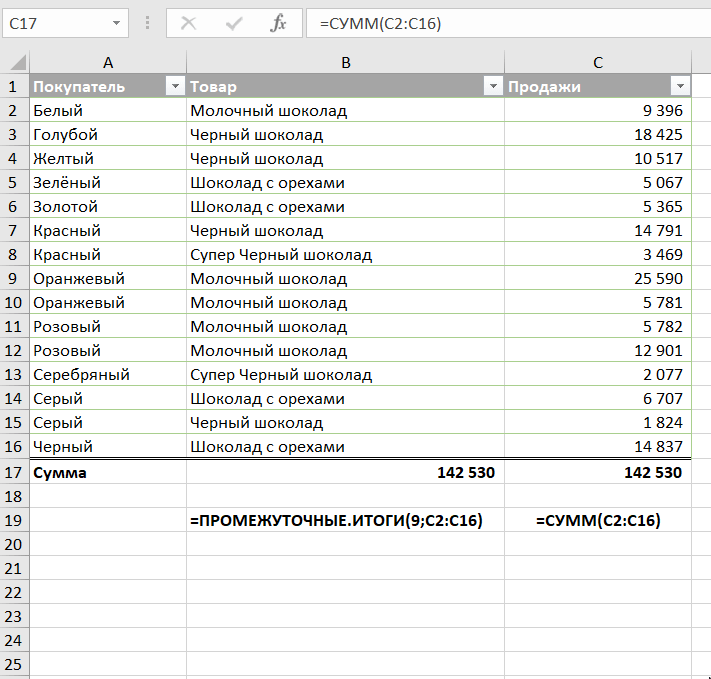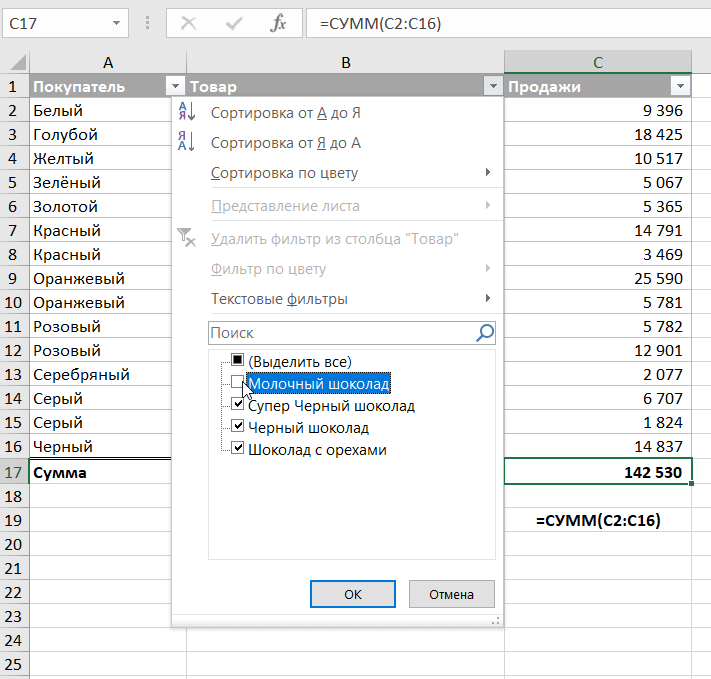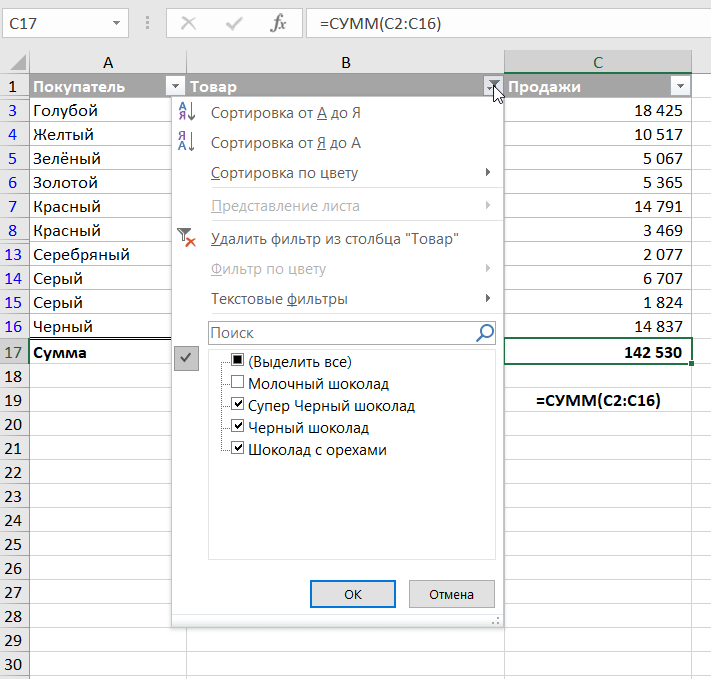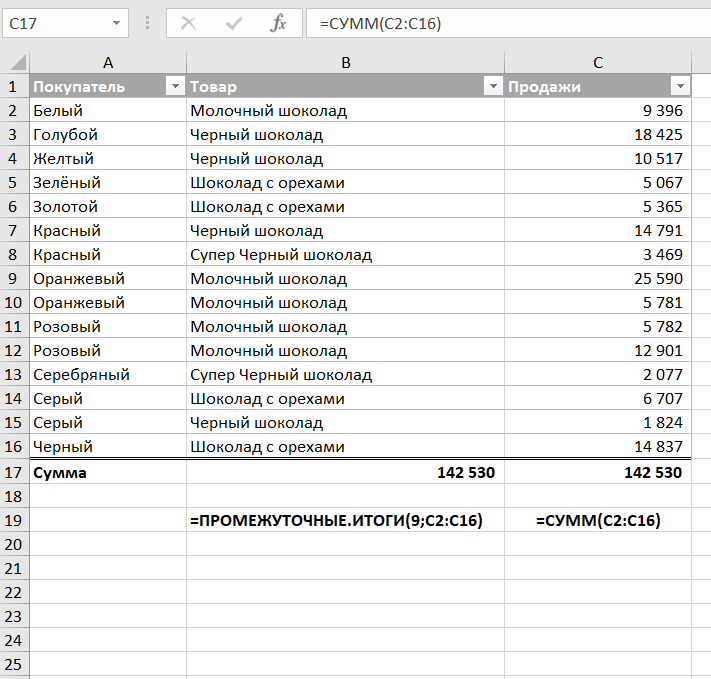
Например, если предположить, что значения для промежуточного итога находятся в ячейках C2: C16, а раскрывающийся список в A17 содержит элементы «Итого», «Среднее», «Максимум» и «Минимум», «динамическая» формула промежуточного итога будет выглядеть следующим образом:
=ЕСЛИ(A17=»Сумма»;ПРОМЕЖУТОЧНЫЕ.ИТОГИ(9;C2:C16); ЕСЛИ(A17=»Среднее»;ПРОМЕЖУТОЧНЫЕ.ИТОГИ(1;C2:C16);ЕСЛИ(A17=»Минимум»;ПРОМЕЖУТОЧНЫЕ.ИТОГИ(5;C2:C16); ЕСЛИ(A17=»Максимум»;ПРОМЕЖУТОЧНЫЕ.ИТОГИ(4;C2:C16);»»))))
И теперь, в зависимости от того, какую функцию ваш пользователь выбирает из раскрывающегося списка, соответствующая функция будет вычислять значения в отфильтрованных строках:
Примечание. Если вдруг раскрывающийся список и ячейка формулы исчезнут с вашего рабочего листа, обязательно снова выберите их в списке фильтра – значит, вы их случайно отфильтровали.
Думаю, при помощи этого способа вы можете заменить этой универсальной функцией стандартные функции суммирования, нахождения максимума и минимума, среднего значения, подсчёта и т.д. Ведь в данном случае даже сортировка не нужна, так как мы не группируем данные, а просто делаем подсчёт. Главное, чтобы не было пустых строк.
Обратите внимание также на то, что если бы мы использовали для расчёта суммы продаж функцию СУММ, то в этой таблице мы не смогли бы подсчитать продажи по какому-то определённому покупателю или группе покупателей. Пришлось бы для каждого из них использовать функцию СУММЕСЛИ.
Вы можете достаточно просто посчитать промежуточные итоги с условием, если отфильтровать нужные строки по товарам, по покупателям либо по другим критериям. Результат будет показан только по значениям, оставшимся после фильтрации. Соответственно и расчет будет сделан только по ним.
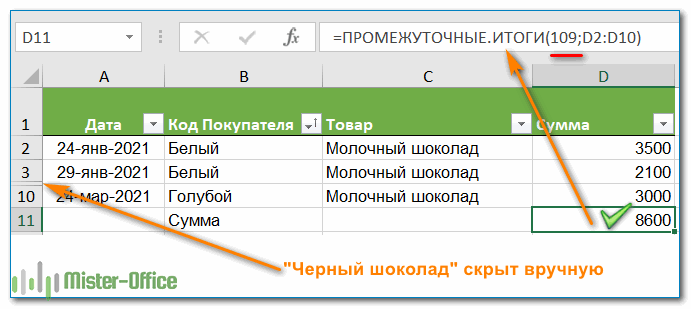
К примеру, вот как можно подсчитать сумму продаж черного шоколада, исключив молочный при помощи фильтра:
Как видите, при помощи СУММ это сделать невозможно. А использовать СУММЕСЛИ — это каждый раз корректировать условие в формуле либо делать несколько формул «на все случаи жизни». А здесь мы просто отбираем нужное при помощи фильтра. Согласитесь, это гораздо проще и удобнее, нежели писать и затем корректировать громоздкие формулы.
Почему промежуточные итоги не работают? Распространенные ошибки.
Если формула промежуточного итога возвращает ошибку, вероятно, это связано с одной из следующих причин:
#ЗНАЧЕН!— аргумент номер_функции не является целым числом от 1 до 11 или от 101 до 111; или любой из аргументов ref содержит трехмерную ссылку сразу на несколько листов вашей рабочей книги.
Совет. Если вы еще не чувствуете себя комфортно с функцией ПРОМЕЖУТОЧНЫЕ.ИТОГИ, вы можете использовать встроенный инструмент ПРОМЕЖУТОЧНЫЙ ИТОГ и автоматически вставлять формулы.