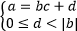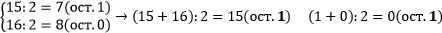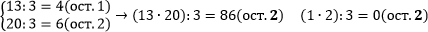Что значит признаки делимости

Признаки делимости чисел

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Что такое «признак делимости»

Признак делимости числа — это такая особенность числа, которая еще до выполнения деления позволяет определить, кратно ли число делителю.

Истинный путь джедая, чтобы зря не пыхтеть над числами, которые в конечном итоге не делятся.

Однозначные, двузначные и трехзначные числа

Однозначное число — это такое число, в составе которого один знак (одна цифра). Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Двузначные числа — такие, в составе которых два знака (две цифры). Цифры могут повторяться или быть различными.

Трехзначные числа — числа, в составе которых три знака (три цифры).

Чётные и нечётные числа

Число называют четным тогда, когда оно делится на два без остатка. А нечетные числа — те, что на два без остатка не делятся. Все просто!

Признаки делимости чисел

Признак делимости на 2. Сразу можно сказать, что число делится на 2, если последняя цифра четная.

Признак делимости на 3. Сумма цифр числа должна делиться на 3.

Признаки делимости на 4. Число делится на 4, если две последние цифры — 0 или если они образуют цифру, которая делится на 4.

Признаки делимости на 5. Число делится на 5, если заканчивается на 0 или 5.

Признак делимости на 6. На 6 делятся те числа, которые могут одновременно делится на 2 и на 3.

Признаки делимости на 8. Число делится на 8, если три последних цифры — 0 или если они образуют число, которое делится на 8.

Признак делимости на 9. Число делится на 9, если сумма цифр делится на 9.

Признаки делимости на 10, 100. Числа, которые заканчиваются на 0, 00, 000 делятся на 10, 100, 1000 и так далее.

Источник

Признаки делимости чисел

В данной публикации мы рассмотрим признаки делимости на числа от 2 до 11, сопроводив их примерами для лучшего понимания.

Признак делимости – это алгоритм, используя который можно сравнительно быстро определить, является ли рассматриваемое число кратным заранее заданному (т.е. делится ли на него без остатка).

Признак делимости на 2

Число делится на 2 тогда и только тогда, когда его последняя цифра является четной, т.е. также делится на два.

Примеры:

Признак делимости на 3

Число делится на 3 тогда и только тогда, когда сумма всех его цифр, также, делится на три.

Примеры:

Признак делимости на 4

Двузначное число

Число делится на 4 тогда и только тогда, когда сумма удвоенной цифры в разряде его десятков и цифры в разряде единиц, также, делится на четыре.

Число разрядов больше 2

Число кратно 4, когда две его последние цифры образуют число, делящееся на четыре.

Примечание:

Число делится на 4 без остатка, если:

Признак делимости на 5

Число делится на 5 тогда и только тогда, когда его последняя цифра – это 0 или 5.

Примеры:

Признак делимости на 6

Число делится на 6 тогда и только тогда, когда он одновременно кратно и двум, и трем (см. признаки выше).

Примеры:

Признак делимости на 7

Число делится на 7 тогда и только тогда, когда сумма утроенного числа его десятков и цифры в разряде единиц, также, делится на семь.

Признак делимости на 8

Трехзначное число

Число делится на 8 тогда и только тогда, когда сумма цифры в разряде единиц, удвоенной цифры в разряде десятков и учетверенной в разряде сотен делится на восемь.

Число разрядов больше 3

Число делится на 8, когда три последние цифры образуют число, делящееся на 8.

Признак делимости на 9

Число делится на 9 тогда и только тогда, когда сумма всех его цифр, также, делится на девять.

Примеры:

Признак делимости на 10

Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.

Примеры:

Признак делимости на 11

Число делится на 11 тогда и только тогда, когда модуль разности сумм четных и нечетных разрядов равен нулю или делится на одиннадцать.

Примеры:

Источник

Делимость чисел. Признаки делимости. Основная теорема арифметики

В этой статье – необходимая теория для решения задачи 18 Профильного ЕГЭ по математике. Но это не все. Знания о числах и их свойствах, признаки делимости и формула деления с остатком могут пригодиться вам при решении многих задач ЕГЭ.
Повторим еще раз, какие бывают числа.

Например, при делении 9 на 4 мы получаем частное 2 и остаток 1, то есть 9 = 4∙2 + 1.

Простые числа – те, что делятся только на себя и на единицу. Единица не является ни простым, ни составным числом. Простые числа: 2, 3, 5, 7, 11, 13, 17, 19…

Числа называются взаимно простыми, если они не имеют общих делителей, кроме 1.

Любое натуральное число можно разложить на простые множители.

Например, 72 = 2∙2∙2∙3∙3, а 98 = 2∙7∙7.

Основная теорема арифметики: Любое натуральное число можно представить в виде произведения простых делителей, взятых в натуральных степенях, причем это разложение единственно.

Наименьшее общее кратное двух чисел (НОК) — это наименьшее число, которое делится на оба данных числа.

Наибольший общий делитель двух чисел (НОД) — это наибольшее число, на которое делятся два данных числа.

последняя цифра числа четная;

сумма цифр числа делится на 3;

число заканчивается на 0 или на 5;

сумма цифр числа делится на 9;

последняя цифра числа равна 0;

суммы цифр на четных и нечетных позициях числа равны или их разность кратна 11.

Источник

Признаки делимости

При решении задач ЕГЭ базового и профильного уровня необходимо знать признаки делимости. Многие признаки делимости чисел нацело вы знаете из начального курса математики. Поэтому такая простая информация могла легко забыться. Сегодня мы с вами повторим основные признаки делимости и решим некоторые задачи.

Признаки делимости

Говорят, что целое число a делится на натуральное число b, если существует такое целое число c, что выполняется равенство a = bc. В этом случае число b называют делителем числа a, а число a — кратным числу b.

Если числа делится на b, то пишут .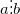

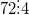
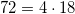
так как так как

Свойства делимости чисел

Простые числа и составные числа.

Простые и составные числа

Число p 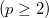называется простым, если оно делится только на себя и на единицу.

Составными числами называются целые числа, имеющие больше двух различных делителей.

Число 17 простое. Делители 17: 1, 17.

Число 9 составное. Делители 9: 1, 3, 9.

Единица не является ни простым, ни составным числом.

Два числа, наибольший делитель которых, равен 1, называются взаимно простыми.

Признаки делимости

Признак делимости на 2

Число делится на 2 тогда и только тогда, когда последняя цифра в записи числа есть число, которое делится на 2 (последняя цифра – образует четное число).

Например, число 124 делится на 2, так как 4 — четное число.

Признак делимости на 4

Число делится на 4 тогда и только тогда, когда последние две цифры числа дают число, которое делится на 4.

Пример: 132 делится на 4, потому что последние две цифры «3» и «2» образуют число 32, которое делится на 4.

Признак делимости на 8

Число делится на 8 тогда и только тогда, когда последние три цифры в записи числа образуют число, которое делится на 8.

Пример, число 2192 делится на 8, поскольку последние три цифры «1», «9» и «2» образуют число 192, которое делится на 8. При рассмотрении задач надо иметь в виду, что число делящееся на 8, в свою очередь должно делится и на 4 и на 2 одновременно.

Признак делимости на 3

Число делится на 3 тогда и только тогда, когда сумма чисел, образованных цифрами в записи числа, делится на 3.

Пример: число 153 делится на 3, так как сумма чисел 1+3+5=9 делится на 3.

Признак делимости на 9

Число делится на 9 тогда и только тогда, когда сумма чисел, образованных цифрами в записи числа, делится на 9.

Пример: число 198 делится на 9, поскольку сумма чисел 1+9+8=18 делится на 9.

Признак делимости на 5

Число делится на 5 тогда и только тогда, когда последняя цифра в записи числа образует число, которое делится на 5 (последняя цифра 0 или 5).

Пример, число 165 делится на 5, так как заканчивается на 5.

Признак делимости на 25

Число делится на 25 тогда и только тогда, когда последние две цифры в записи числа, образуют число, которое делится на 25.

Пример: число 125 делится на 25, так как последние две цифра «2» и «5» образуют число 25, которое делится на 25.

Следует помнить, что цифры не могут суммироваться, делиться и т.д. Цифры это такие значки, которыми записываются числа. И веса у них самих по себе не более чем у любого другого значка, как у смайлика. Но, если мы цифрой запишем число, то с числом мы уже можем проводить любые операции. Числа могут быть однозначные и двузначные, их бесконечное количество, но цифр для их записи всего 10. Не путайте понятия числа и цифры, не портите отношения с проверяющими ваши работы математиками.

Признак делимости на 11

Число делится на 11 тогда и только тогда, когда разность суммы чисел, стоящих на нечетных местах в записи числа, и суммы чисел, стоящих на четных местах в записи числа, делится на 11. А также если сумма чисел стоящих на четных местах, делится на сумму чисел, стоящих на нечетных местах.

Пример 1.

123456789 делится на 3, так как 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45, а 45 делится на 3.

Пример 2.

1452 делится на 11, так как (1 + 5) – (4 + 2) делится на 11. Или 1+5=4+2.

Деление с остатком

Пусть a и b ≠ 0 – два целых числа. Разделить число a на число b с остатком – это значит найти такие числа c и d, что выполнены следующие условия:

От деления на b могут быть только остатки: 0, 1, 2, 3…, |b|-1.

Пример 1.

Пример 2.

Пример 3.

Теоремы

1) Сумма чисел a и b даёт тот же остаток при делении на число m, что и сумма остатков чисел a и b при делении на число m.

2) Произведение чисел a и b даёт тот же остаток при делении на число m, что и произведение остатков чисел a и b при делении на число m.

Теперь рассмотрим конкретные задания из ЕГЭ на делимость

Задание №1

Найдите четырёхзначное число, которое делится на 33 и состоит только из цифр 1 и 2. В ответе укажите наименьшее из таких чисел.

Решение:

Если число делится на 33 то оно делиться на 11 и 3. Число делится на 11, если сумма цифр стоящих на четных позициях будет равна сумме цифр на нечетных позициях. Число делится на 3, если сумма цифр делится на 3.

Значит стоит чередовать 1 и 2 по 2 раза, причем если сложим 2 двойки и 2 единицы получим 6, значит, число будет делиться на 3. Получим число 1122.

Ответ: 1122

Задание №2

Найдите трёхзначное число, состоящее только из чётных цифр и кратное 9. В ответе укажите наименьшее из таких чисел.

Решение:

Если число должно делиться на 9, то и сумма цифр должна делиться на 9, наименьшее 9, но его нельзя представить как сумму 3 чётных цифр, рассмотрим 18, первой цифрой поставим 2 ( минимальное четное число), тогда на остальные 2 остается только 8 и 8, получим число 288.

Ответ: 288

Задание №3

Найдите трёхзначное число, которое при делении на 5 и 7 даёт равные ненулевые остатки, а вторая цифра этого числа равна сумме первой и третьей цифр. В ответе укажите какое-нибудь одно такое число.

Решение:

Число не должно оканчиваться на 0 или 5, так как в этом случае остаток от деления на 5 равен 0. Пусть вторая цифра в числе будет 4, тогда первая и третья цифры могут быть 1 и 3, получаем число 143. Проверяем:

1) 143:5=28 (Остаток 3)

2) 143:7=20 (Остаток 3)

Остатки равны, соответственно условие выполнено.

Аналогичными рассуждениями можно найти и другие числа: 176; 352; 561.

Ответ: 176

Задание №4

Найдите трёхзначное число, сумма цифр которого равна 7, если известно, что число содержит цифру 1, и квадрат этого числа делится на 25. В ответе укажите какое-нибудь одно такое число.

Решение:

Если квадрат числа делится на 25, то само число должно делиться на 5. Признак делимости на 5: число делиться на 5, если его последняя цифра 0 или 5. У нас трехзначное число, пусть последняя цифра будет 5, а первая 1, вторая цифра должна быть такой, чтобы сумма цифр была равна 7. Сумма цифр уже 6, то есть вторая цифра должна быть равна 1. Получим число 115.

Аналогичными рассуждениями можно получить числа 160 и 610.

Ответ: 115

Задание №5

Найдите четырёхзначное число, кратное 9, но не кратное 6, произведение цифр которого равно 1960. В ответе укажите какое-нибудь одно такое число.

Решение:

Чтобы число делилось на 9, но не делилось на 6, оно должно быть нечетным.

Разложим 1960 на простые множители: 1960=2*2*2*5*7*7=8*5*7*7

Эти цифры обозначают числа, которые в сумме дают 27, значит число будет делиться на 9. Составим из этих цифр нечетное число, например: 7785.

Аналогичными рассуждениями (простой перестановкой цифр) можно получить другие числа.

Ответ: 7785

Задание №6

Сумма четырёх последовательных трёхзначных чисел равна 458. Найдите третье число.

Решение:

Все 4 числа приблизительно равны между собой, поэтому разделив 458 на 4 получаем 114 с остатком 2. Начинаем подбирать числа от 114.

114+115+116+117=462, это больше 458, начинаем считать от 113.

113+114+115+116=458, получили необходимую сумму. Третье число в данной последовательности равно 115.

Можно было решить альтернативно.

Пусть первое число равно n. Тогда следующие числа n+1, n+2, n+3.

Составим и решим уравнение:

Тогда третье число 115.

Ответ: 115

Задание №7

Найдите трёхзначное число, у которого сумма цифр, стоящих на нечетных местах, кратна 5, а само число кратно 9. В ответе запишите наименьшее такое число.

Решение:

Так как число должно быть наименьшим, то будет подбирать цифры так, чтобы оно начиналось с минимальной цифры (1 и далее), и аналогично будем подбирать для всех разрядов.

Нечетные места это 1 и 3, чтобы сумма цифр на нечетных местах была кратна 5, она должна быть равна, 5, 10 или 15. Пусть она будет равна 5, в сумме 5 составляют числа 1 и 4. Тогда чтобы число делилось на 9 сумма цифр должна делиться на 9, то есть в нашем случае сумма цифр должна равняться 9. То есть, на 2 месте должна стоять цифра 4. Получим число 144.

Ответ: 144

Задание №8

Найдите трёхзначное число, делящееся на 9, если известно, что его цифры являются последовательными членами возрастающей арифметической прогрессии. В ответе укажите какое-нибудь одно такое число.

Решение:

Чтобы число делилось на 9, необходимо чтобы сумма его цифр делилась на 9. А, учитывая, что его цифры должны являться членами возрастающей арифметической прогрессии, каждая цифра должна отличаться от предыдущей на одно и то же число.

Если разность прогрессии равна 1, получаем a, a+1, a+2. Сумма равна 3a+3.

3a+3=9,тогда a=2, а число 234

3a+3=18,тогда a=5, а число 567

Если разность прогрессии равна 2, получаем a, a+2, a+4. Сумма равна 3a+6.

3a+6=9,тогда a=1, а число 135

3a+6=18,тогда a=4, а число 468

3a+6=27, тогда а=7, но следующие члены уже больше 10, не подходит.

Если разность прогрессии равна 3, получаем a, a+3, a+6. Сумма равна 3a+9.

3a+9=9,тогда a=0, не подходит

3a+9=18,тогда a=3, а число 369

3a+9=27,тогда a=6, но следующие члены уже больше 10, не подходит.

Если разность прогрессии равна 4, получаем a, a+4, a+8. Сумма равна 3a+12.

3a+12=18,тогда a=6, но следующие члены уже больше 10, не подходит.

Ответ: 234 или 567, или 135, или 468, или 369.

Задание №9

Найдите четырёхзначное число, которое состоит только из цифр 0 и 2 и делится на 12.

Решение:

Чтобы число делилось на 12, оно должно делиться на 3 и 4. На 3 число делится, если сумма цифр делится на 3. А на 4 делится, если 2 последние цифры нули или образуют число, которое делится на 4.

Чтобы число делилось на 3, в нем должно быть три двойки (чтобы в сумме давали 6). Значит 0 только один, последние 2 цифры должны быть 20, чтобы полученное число делилось на 4. То есть получаем число 2220.

Ответ: 2220

Итак, мы подробно рассмотрели делимость чисел, признаки делимости чисел и поучились применять полученные знания в задании №19 базового уровня егэ по математике.

Источник

Что значит признаки делимости

Признак делимости на 2 n
Число делится на n-ю степень двойки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень.

Признак делимости на 5 n
Число делится на n-ю степень пятёрки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень.

Признак делимости на 10 n +1
Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) и найдем сумму этих групп с переменными знаками, считая их n-числами. Эта сумма делится на 10 n + 1 тогда и только тогда, когда само число делится на 10 n + 1.

Признак делимости на 2
Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной.

Признак делимости на 3
Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.

Признак делимости на 4
Число делится на 4 тогда и только тогда, когда число из двух последних его цифр нули или делится на 4.

Признак делимости на 5
Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5 (то есть равна 0 или 5).

Признак делимости на 6
Число делится на 6 тогда и только тогда, когда оно делится на 2 и на 3.

Признак делимости на 7
Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7 (например, 259 делится на 7, так как 25 — (2 · 9) = 7 делится на 7).

Признак делимости на 9
Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.

Признак делимости на 10
Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.

Признак делимости на 12
Число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4.

Признак делимости на 13
Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно 13 (например, 845 делится на 13, так как 84 + (4 · 5) = 104 делится на 13).

Признак делимости на 14
Число делится на 14 тогда и только тогда, когда оно делится на 2 и на 7.

Признак делимости на 15
Число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5.

Признак делимости на 17
Число делится на 17 тогда и только тогда, когда число его десятков, сложенное с увеличенным в 12 раз числом единиц, кратно 17 (например, 29053→2905+36=2941→294+12=306→30+72=102→10+24=34. Поскольку 34 делится на 17, то и 29053 делится на 17). Признак не всегда удобен, но имеет определенное значение в математике. Есть способ немного попроще – Число делится на 17 тогда и только тогда, когда разность между числом его десятков и упятеренным числом единиц, кратно 17(например, 32952→3295-10=3285→328-25=303→30-15=15. поскольку 15 не делится на 17, то и 32952 не делится на 17)

Признак делимости на 19
Число делится на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19 (например, 646 делится на 19, так как 64 + (6 · 2) = 76 делится на 19).

Признак делимости на 23
Число делится на 23 тогда и только тогда, когда число его сотен, сложенное с утроенным числом десятков, кратно 23 (например, 28842 делится на 23, так как 288 + (3 * 42) = 414 продолжаем 4 + (3 * 14) = 46 очевидно делится на 23).

Признак делимости на 25
Число делится на 25 тогда и только тогда, когда две его последние цифры делятся на 25 (то есть образуют 00, 25, 50 или 75)или число кратно 5.

Признак делимости на 99
Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп, считая их двузначными числами. Эта сумма делится на 99 тогда и только тогда, когда само число делится на 99.

Признак делимости на 101
Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп с переменными знаками, считая их двузначными числами. Эта сумма делится на 101 тогда и только тогда, когда само число делится на 101. Например, 590547 делится на 101, так как 59-05+47=101 делится на 101).

Рейтинг: 3.5/5 (Всего оценок: 207)

Источник