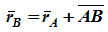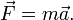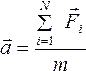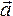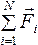Что значит поступательное движение в физике
Поступательное движение
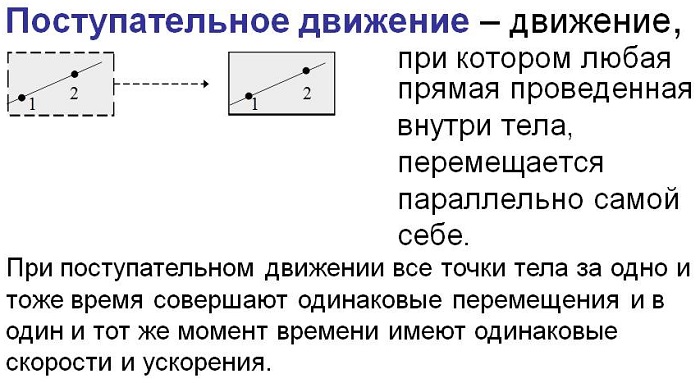
Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени. [1]
В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе, остаётся в силе.
Математически поступательное движение по своему конечному результату эквивалентно параллельному переносу.Однако, рассматриваемое как физический процесс оно представляет собой в трёхмерном пространстве вариант винтового движения (См. Рис. 2)
Содержание
Примеры поступательного движения
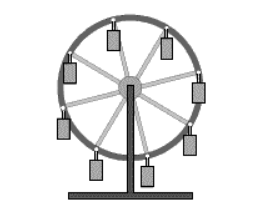
Поступательно движется, например, кабина лифта. Также, в первом приближении, поступательное движение совершает кабина колеса обозрения. Однако, строго говоря, движение кабины колеса обозрения нельзя считать поступательным.
В соответствие с первым и вторым законами Ньютона кабина, стремясь сохранить направление своего движения, отклоняется от вертикальной прямой, причём в разном направлении по разные стороны от оси симметрии колеса обозрения. Таким образом, не всякая прямая, связанная с кабиной, перемещается параллельно самой себе. Причём отклонение кабины от вертикальной прямой, и соответственно, отклонение траектории движения кабины от траектории поступательного движения тем больше, чем больше частота вращения колеса обозрения. Учитывая, что реальные частоты вращения колёс обозрения достаточно малы, траектории движения их кабин весьма близки к траектории поступательного движения. Этим можно объяснить, что во многих источниках движение кабины приводится в качестве примера поступательного движения.
Моделью поступательного движения в первом приближении (если пренебречь качанием ступни) является педаль велосипеда, совершающая при этом за полный цикл своего хода один поворот вокруг своей оси.
Связь движения тела и движения его точек
Если тело движется поступательно, то для описания его движения достаточно описать движение произвольной его точки (например, движение центра масс тела).
Одной из важнейших характеристик движения точки является её траектория, в общем случае представляющая собой пространственную кривую, которую можно представить в виде сопряжённых дуг различного радиуса, исходящего каждый из своего центра, положение которого может меняться во времени. В пределе и прямая может рассматриваться как дуга, радиус которой равен бесконечности.
В таком случае оказывается, что при поступательном движении в каждый заданный момент времени любая точка тела совершает поворот вокруг своего мгновенного центра поворота, причём длина радиуса в данный момент одинакова для всех точек тела. Одинаковы по величине и направлению и векторы скорости точек тела, а также испытываемые ими ускорения.
При решении задач теоретической механики бывает удобно рассматривать движение тела как сложение движения центра масс тела и вращательного движения самого тела вокруг центра масс (это обстоятельство принято во внимание при формулировке теоремы Кёнига).
объясните русским языком: что такое поступательное движение тела?
Принцип поступательного движения реализован в чертёжном приборе — пантографе, ведущее и ведомое плечо которого всегда остаются параллельными, то есть движутся поступательно. При этом любая точка на движущихся частях совершает в плоскости заданные движения, каждая вокруг своего мгновенного центра вращения с одинаковой для всех движущихся точек прибора угловой скоростью.
Существенно, что ведущее и ведомое плечо прибора, хотя и движущиеся согласно, представляют собой два разных тела. Поэтому радиусы кривизны, по которым движутся заданные точки на ведущем и ведомом плече могут быть сделаны неодинаковыми, и именно в этом и заключается смысл использования прибора, позволяющего воспроизводить любую кривую на плоскости в масштабе, определяемым отношением длин плеч.
Рис 1.Поступательное движение тела на плоскости слева-направо, с произвольно выделенным в нём отрезком AB. Вначале прямолинейное, затем — криволинейное, переходящее во вращение каждой точки вокруг своего центра с равными для данного момента угловыми скоростями и равными значениями радиуса поворота. Точки O — мгновенные центры поворота вправо. R — их равные для каждого конца отрезка, но различные для разных моментов времени мгновенные радиусы поворота.
Поступательное движение — это механическое движение системы точек (абсолютно твёрдого тела), при котором отрезок прямой, связывающий две любые точки этого тела, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени [1].
Приведённая иллюстрация показывает, что вопреки распространённому утверждению [2], поступательное движение не является противоположностью движению вращательному, а в общем случае может рассматриваться как совокупность поворотов — не закончившихся вращений. При этом подразумевается, что прямолинейное движение есть поворот вокруг бесконечно удалённого от тела центра поворота.
В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе, остаётся в силе.
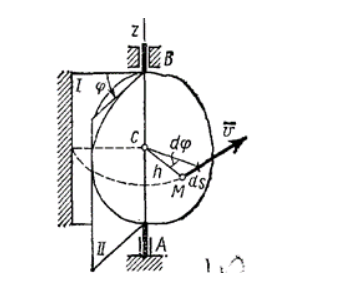
Математически поступательное движение по своему конечному результату эквивалентно параллельному переносу. Однако, рассматриваемое как физический процесс, оно представляет собой в трёхмерном пространстве вариант винтового движения (См. Рис. 2)
Содержание [убрать]
1Примеры поступательного движения
2Связь движения тела и движения его точек
3Примеры устройств
4См. также
5Примечания
6Литература
7Ссылки
Примеры поступательного движения [править | править вики-текст]
Поступательно движется, например, кабина лифта. Также, в первом приближении, поступательное движение совершает кабина колеса обозрения. Однако, строго говоря, движение кабины колеса обозрения нельзя считать поступательным.
В соответствие с первым и вторым законами Ньютона кабина, стремясь сохранить направление своего движения, отклоняется от вертикальной прямой, причём в разном направлении по разные стороны от оси симметрии колеса обозрения. Таким образом, не всякая прямая, связанная с кабиной, перемещается параллельно самой себе. Причём отклонение кабины от вертикальной прямой, и соответственно, отклонение траектории движения кабины от траектории поступательного движения тем больше, чем больше частота вращения колеса обозрения. Учитывая, что реальные частоты вращения колёс обозрения достаточно малы, траектории движения их кабин весьма близки к траектории поступательного движения. Этим можно объяснить, что во многих источниках движение кабины приводится в качестве примера поступательного движения.
Моделью поступательного движения в первом приближении (если пренебречь качанием ступни) является педаль велосипеда, совершающая при этом за полный цикл своего хода один поворот вокруг своей оси.
Связь движения тела и движения его точек [править | править вики-текст]
Если тело движется поступательно, то для описания его движения достаточно описать движение произвольной его точки (например, движение центра масс тела).
Одной из важнейших характеристик движения точки является её траектория, в общем случае представляющая собой пространственную кривую, которую можно представить в виде сопряжённых дуг различного радиуса, исходящего каждый из своего центра, положение которого может меняться во времени. В пределе и прямая может рассматриваться как дуга, радиус которой равен бесконечности.
Рис. 2 Пример Трёхмерного поступательного движения тела
В таком случае оказывается, что при поступательном движении в каждый заданный момент времени любая точка тела совершает поворот вокруг своего мгновенного центра по
Поступательное движение — это механическое движениесистемы точек (абсолютно твёрдого тела), при котором отрезок прямой, связывающий две любые точки этого тела, форма и размеры которого во время движения не меняются
Поступательное движение-движение при котором в любой момент времени все точки одного тела движутся одинаково.
Допустим едет тележка, в любой момент времени какую точку тележки мы не возьмем её траектория движения будет такая же как и у любой другой взятой точки этой же тележки, не смотря на то, что тележка будет ехать по неровной поверхности
Поступательное и вращательное движение
Движение твердого тела разделяют на виды:
Первые два из них – простейшие, а остальные представляют как комбинацию основных движений.
Поступательное криволинейное движение. Угол поворота тела
Поступательным называют движение твердого тела, при котором любая прямая, проведенная в нем, двигается, оставаясь параллельной своему начальному направлению.
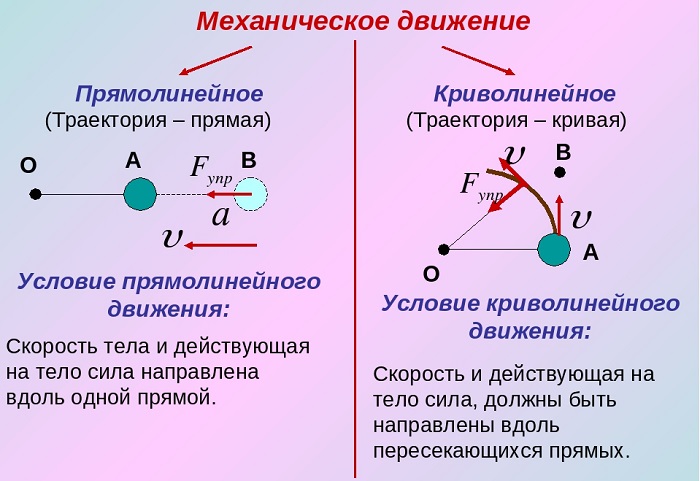
Прямолинейное движение является поступательным, но не всякое поступательное будет прямолинейным. При наличии поступательного движения путь тела представляют в виде кривых линий.
Свойства поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые траектории и в каждый момент времени обладают одинаковыми по модулю и направлению значениями скорости и ускорения.
Следовательно, поступательное движение твердого тела определено движением любой его точки. Это сводится к задаче кинематики точки.
Понятие о скорости и ускорении тела имеют смысл только при наличии поступательного движения. В других случаях точки тела характеризуются разными скоростями и ускорениями.
Вращательное движение абсолютно твердого тела вокруг неподвижной оси – это движение всех точек тела, находящихся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывание окружностей, центры которых располагаются на этой оси.
При наличии такого вращения значения углов поворота радиус-вектора различных точек тела будут аналогичны.
Вращательное и поступательное движение. Формулы
| Поступательное | Вращательное |
| Равномерное | |
| s = υ · t | φ = ω · t |
| υ = c o n s t | ω = c o n s t |
| a = 0 | ε = 0 |
| Равнопеременное | |
| s = υ 0 t ± a t 2 2 | φ = ω 0 t ± ε · t 2 2 |
| υ = υ 0 ± a · t | ω = ω 0 ± ε · t |
| a = c o n s t | ε = c o n s t |
| Неравномерное | |
| s = f ( t ) | φ = f ( t ) |
| υ = d s d t | ω = d φ d t |
| a = d υ d t = d 2 s d t 2 | ε = d ω d t = d 2 φ d t 2 |
Задачи на вращательное движение
Решение
Решение
Поступательное движение в школьной программе изучает предмет физика. Для понимания, что оно собой представляет, каким законам подчиняется, изучим основную терминологию и рассмотрим понятие на конкретных примерах, которые встречаются в повседневной жизни.
Что такое поступательное движение
Перемещение твердого тела (всех взаимосвязанных его точек) с помощью механического воздействия по заданной траектории и в определенном направлении, в результате которого отрезок из двух любых точек данного тела будет всегда параллелен своему расположению, предшествующему нынешнему, в каждый отрезок времени, называется поступательным движением.
В процессе перемещения характеристика объекта не меняется: по составу, форме и величинам сторон. Причем в любой отрезок времени точки объекта обладают одним и тем же направлением модулей векторов скорости и ускорения, а их величины равны.
Выделяют прямолинейное поступательное движение и криволинейное.
В качестве примеров поступательного движения в можно привести функционирование по определенной траектории различного оборудования и механизмов.
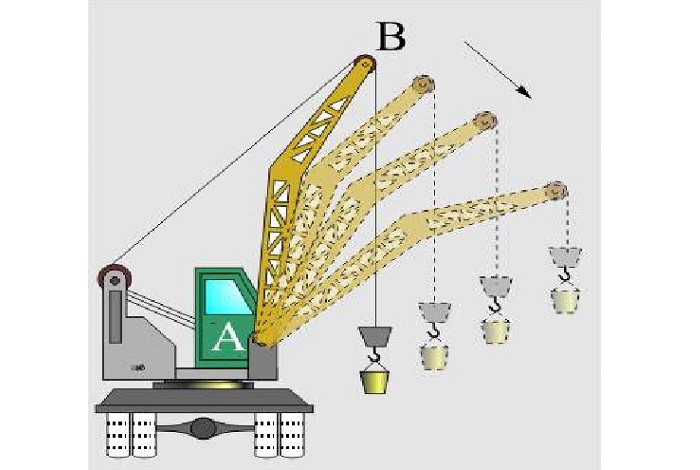
перемещение стрелы с грузом строительного подъемного крана относительно его кабины, в которой сидит рабочий;
подъем и спуск лифта в шахте;
педали у велосипеда. При этом каждая его точка, напротив, совершает вращательные движения;
совершение кабиной оборотов на колесе обозрения в парках аттракционов.
Теорема о поступательном движении
Материальные точки объекта (тела), осуществляющего поступательные движения, перемещаются по одному и тому же пути, а скорости и ускорения в каждый промежуток времени совпадают по модулю вектора и направлению.
Доказательство теоремы
Докажем данную теорему. Для этого необходимо провести прямую линию через две любые точки твердого тела, осуществляющего поступательное движение – пусть это будут точки А и В.
Полученный отрезок АВ совершает перемещение по заданному пути: А описывает траекторию АА1А2А3Аn, а В соответственно – В1В2В3Вn.
Отсюда следует, что:
Принимая во внимание, что размеры данного отрезка АВ неизменны (const) при перемещении, а сам он имеет свойство двигаться в пространстве параллельно своему предыдущему местоположению, значит направления точки А и точки В совпадают.
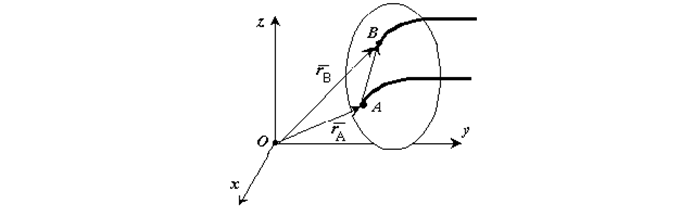
Соотношение радиусов-векторов точек А и В в системе координат относительно ее начала – О (Рис 1),
можно выразить формулой:
где линии пути точки А соответствует функция rA(t), точки B – rB(t).
Теорема доказывает, что для определения поступательного движения твердого материального объекта достаточно знать параметры перемещения любой одной его точки. Следовательно, изучая кинематику передвижения точки тела, решается задача определения поступательного движения.
Основной закон динамики поступательного движения
Основной закон динамики поступательного движения трактует II закон Ньютона.
Формулировка закона звучит следующим образом:
Совокупность равнодействующих сил, оказывающих воздействие на материальное тело, способствует возникновению ускорения. То есть, ускорение прямо пропорционально векторному суммарному значению оказываемых на него сил, и обратно пропорционально массе объекта.
Основное уравнение закона приведено ниже:
Причем у равнопеременного движения векторное ускорение
II закон Ньютона работает исключительно в ИСО (инерциальная система отсчета), где объекты двигаются равномерно, прямолинейно или находятся в состоянии покоя.
Кинематика. Поступательное движение.
Поступательное движение – это движение твердого тела, при котором прямая, соединяющая две любые точки тела, остается параллельной самой себе.
Чтобы изучать изменения положения тела в пространстве, нужно уметь определять само это положение. Как известно, у каждого тела определенные размеры, следовательно, разные точки этого тела находятся в разных местах пространства. Как же определить положение всего тела? В основном, указывать положение каждой точки движущегося тела нет необходимости, особенно если все точки тела движутся одинаково.
Например, зачем описывать движение каждой точки спускающихся с горы санок, если эти движения ничем не различаются между собой.
Движение тела, при котором все его точки движутся одинаково, называют поступательным.
При поступательном движении все точки тела движутся по одинаковым траекториям, параллельным друг другу, с одинаковыми в каждый момент времени по модулю и направлению скоростями и ускорениями. Общая скорость всех точек называется скоростью поступательного движения, а общее ускорение всех точек – ускорением поступательного движения.
Поступательное движение бывает как криволинейным, так и прямолинейным.
Например, поступательно движется человек, находящийся в кабине лифта, или чемодан, который поднимают с пола. Для описания его движения достаточно рассмотреть движение только одной его точки.
Другими словами, изучение поступательного движения твердого тела сводится к задаче кинематики точки.