Что значит построить сечение

Что значит построить сечение

Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырехугольники (рис. 1). Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники (рис. 2).

Теоремы, используемые при построении сечений

Теорема 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Поэтому секущая плоскость пересекает плоскости параллельных граней по параллельным прямым.

Теорема 2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Теорема 3. Если прямая l параллельна какой либо прямой m, проведённой в плоскости то она параллельна и самой плоскости

Теорема 4. Если прямая, лежащая в плоскости сечения, не параллельна плоскости некоторой грани, то она пересекается со своей проекцией на эту грань.

Алгоритм построения сечений

Для построения сечений рекомендуем пользоваться следующим алгоритмом.

1. Если две точки секущей плоскости лежат в плоскости одной грани, то проводим через них прямую. Часть прямой, лежащая в плоскости грани — сторона сечения.

2. Если прямая a является общей прямой секущей плоскости и плоскости какой-либо грани, то находим точки пересечения прямой a с прямыми, содержащими ребра этой грани. Полученные точки — новые точки секущей плоскости, лежащие в плоскостях граней.

3. Если никакие две из данных точек не лежат в плоскости одной грани, то строим вспомогательное сечение, содержащее любые две данные точки, а затем выполняем шаги 1, 2.

Для контроля правильности построенного сечения, проверяйте, что:

– все вершины сечения лежат на рёбрах многогранника;

– все стороны сечения лежат в гранях многогранника;

– в каждой грани многогранника лежит не более одной стороны сечения.

Источник

Что значит построить сечение

Правила построения сечений многогранников:

1) проводим прямые через точки, лежащие в одной плоскости;

2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого

а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);

б) параллельные грани плоскость сечения пересекает по параллельным прямым.

Примеры построения сечений:

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Построим сечение, проходящее через точки M, N, L.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

Пересечем прямую ML ( принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

Найдем прямую пересечения плоскости сечения с плоскостью DD₁C₁C:

пересечем прямую ML (принадлежащую сечению) с ребром DD₁, они лежат в одной плоскости AA₁D₁D, получим точку X₂;

пересечем прямую KN (принадлежащую сечению) с ребром D₁C₁, они лежат в одной плоскости A₁B₁C₁D₁, получим точку X₃;

Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.

.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

.

Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.

.

Пересечем прямую ML ( принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

.

Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).

.

Соединим точки P и L ( они лежат в одной плоскости).

.

Источник

Урок геометрии по теме: «Построение сечений в многогранниках методом следов». 10-й класс

Разделы: Математика

Класс: 10

Девиз: “Мы одна семья, мы учимся все вместе”

Обучающая цель: формирование умений и навыков построения сечений методом следов.

Воспитывающая цель: воспитывать чувство сплоченности, взаимопомощи, воспитывать умения работать индивидуально над задачей.

Тип урока: урок формирования и совершенствования знаний.

Формы организации учебной деятельности: групповая, индивидуальная, коллективная.

Техническое обеспечение урока: мультимедийный проектор, набор геометрических тел (куб, параллелепипед, пирамида).

Организационный момент: Рассаживаемся на 3 группы по 5 человек. На каждом столе – набор тел, памятки-опоры, карточки для индивидуальной работы по построению сечений.

Слово учителя: Вы изучили аксиомы стереометрии, следствия из аксиом, теоремы о параллельности прямых и плоскостей в пространстве. При решении многих стереометрических задач используют сечение многогранника плоскостью. Существует несколько методов построения сечений многогранника плоскостью: метод следов, метод внутреннего проектирования и комбинированный метод.

Мы изучим метод следов.

1) Ребята, я предлагаю вам повторить и вспомнить некоторые геометрические понятия и определения.

2) Ребята, перед вами пример неправильного построения сечения куба АС1 плоскостью, проходящей через заданные точки N, C, D1.

А рядом сечение построено верно.

На уроках черчения вы пользовались определением: Сечение – это изображение фигуры, которая получается при мысленном рассечении тела плоскостью.

Вот таким определением мы и будем пользоваться сегодня на уроке.

В тетраэдре сечениями могут быть только треугольники или четырехугольники, а в параллелепипеде – треугольники, четырехугольники, пятиугольники или шестиугольники.

Рассмотрим пример (мультимедийный проектор).

Построить сечение куба, проходящее через точки М, N, L.

Алгоритм построения

Источник

ИНТЕРАКТИВНЫЕ МОДЕЛИ В ОБУЧЕНИИ

Пример: модели МК в электронном учебнике

Сечения многогранников

ТЕОРИЯ

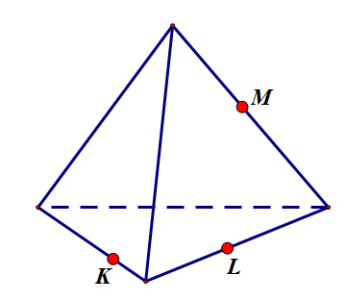
В этом разделе мы рассмотрим методы построения сечений многогранников. Плоскость сечения, как правило, будет задаваться тремя точками – K, L, M. Сложность такой задачи во многом определяется расположением точек, задающих плоскость сечения.

Пример 1

Самый простой случай – когда точки лежат на трёх смежных рёбрах пирамиды – не нуждается в разборе.

Основной метод, который используется при построении сечений, называется методом следов.

Следом называется прямая, по которой плоскость сечения пересекает плоскость любой из граней многогранника. Если такой след найден, то точки его пересечения с соответствующими рёбрами многогранника и будут вершинами искомого сечения.

Пример 2

Пусть теперь точки K и M лежат на боковых рёбрах пирамиды, а точка L – на стороне основания.

Пример 3

Использованный на первом шаге построения приём часто называют методом вспомогательных плоскостей. Рассмотрим ещё один пример, где он используется.

Пример 4

Рассмотрим теперь самый общий случай, когда все три точки K, L и M лежат на гранях пирамиды.

С помощью метода вспомогательных плоскостей можно строить сечения, «не выходя» за пределы многогранника. Вернёмся в связи с этим к примеру 2.

Пример 2’

Точки K и M лежат на боковых рёбрах пирамиды, а точка L – на стороне основания. Построим сечение, «не выходя» за пределы многогранника.

Можно использовать ту же самую идею иначе. Проведём в начале анализ построенного сечения – т.е. начнём с конца. Допустим, что по точкам K, L и M построено сечение KLMN.

Обозначим через F точку пересечения диагоналей четырёхугольника KLMN. Проведём прямую CF и обозначим через F₁ точку её пересечения с гранью SAB. С другой стороны, точка F₁ совпадает с точкой пересечения прямых KB и MA, исходя из чего её и можно построить.

Использованный в этом решении приём называют методом внутреннего проектирования. Построим с его помощью сечение из примера 4, когда все три точки лежат на гранях пирамиды.

Пример 3’

Точки K, L и M лежат на гранях пирамиды. Построим сечение, «не выходя» за пределы многогранника.

Допустим, что сечение уже построено.

Пусть плоскость сечения пересекает ребро CB в точке P. Обозначим через F точку пересечения KM и LP. Построим центральные проекции точек K, F и M из точки C на плоскость SAB и обозначим их K₁, F₁ и M₁. Точки K₁ и M₁ легко находятся, а точку F₁ можно получить как точку пересечения K₁M₁ и LB.

УПРАЖНЕНИЯ

Более сложные упражнения помечены звёздочкой.

1. Постройте сечение треугольной пирамиды плоскостью, проходящей через точки K, L и M (см. модели).

a

b

c

d

2. Постройте сечение куба плоскостью, проходящей через точки K, L и M (см. модели).

a

b

c

d

e

3. На рёбрах пирамиды SABC отмечены точки K, L и M. Постройте:

(a) прямую, по которой пересекаются плоскости CSK и MLA;

(b) точку пересечения плоскостей ACM, CSK и ASL;

(c) точку пересечения плоскостей AML, CKM и SKL.

4*. На рёбрах пирамиды SABC отмечены точки K, L, M, P, N и Q. Постройте:

(a) прямую, по которой пересекаются плоскости KLM и PNQ;

(b) точку пересечения плоскостей ALM, CNP и SKQ.

5*. На ребре AB треугольной пирамиды SABC отмечена точка K. Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной BC и SA.

6*. На рёбрах AB и CS треугольной пирамиды SABC отмечены точки K и M. Постройте сечение пирамиды плоскостью, проходящей через точки K и M и параллельной AS.

7*. Постройте сечение треугольной пирамиды плоскостью, проходящей через точки K, L и M, лежащих в плоскостях её боковых граней (но не на самих гранях!).

8*. На плоскости проведены три луча с общим началом – a, b и с – и отмечены три точки – A, B и C. Постройте треугольник, вершины которого лежат на этих лучах, а стороны проходят через точки A, B и C.

Источник

Учимся строить сечения многогранников. Часть 2.

Учимся строить сечения многогранников. Часть 2.

Эта статья для тех, кто хочет научиться строить сечения. Она содержит 11 заданий для построения сечений, подсказки и ответы к каждому заданию. Рекомендую сначала прочитать эту статью и посмотреть это видео.

Чтобы найти точку, лежащую одновременно в двух плоскостях, нужно найти точку пересечения прямой, лежащей в первой плоскости, с прямой, лежащей во второй плоскости.

В подсказках и ответах изображение дополнительных прямых, используемых при построении сечения, сплошными линиями или пунктирными, не зависит от того, видимы эти прямые или нет.

Рядом с каждой дополнительной прямой указан ее порядковый номер при построении сечения. Все прямые проведены через две точки, принадлежащие определенной плоскости. Прямые пронумерованы в порядке их построения. Рекомендуется при использовании подсказки и воспроизведении построения сечения проговаривать, какой плоскости принадлежит данная прямая, каким плоскостям принадлежит точка их пересечения.

Постройте сечения, проходящие через точки .

Задание 1:

Источник