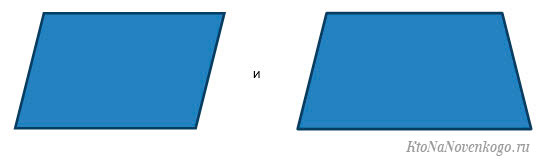
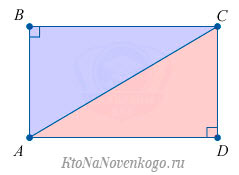
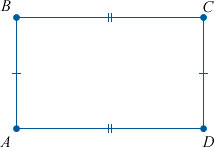
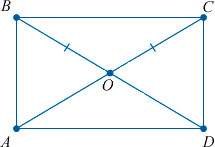
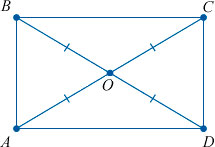
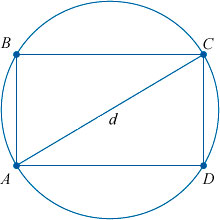
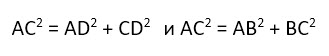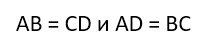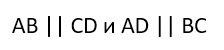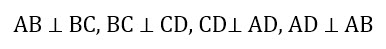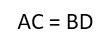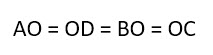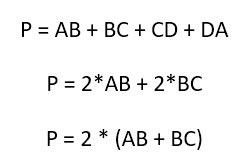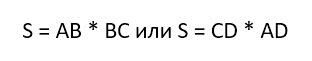Что значит попарно различные прямоугольники
Задание №19 Т/Р №176 А. Ларина
Смотрите также №13; №14; №15; №16; №17; №18 Тренировочной работы №176 А. Ларина
19. Дан клетчатый квадрат размером 6х6.
а) Можно ли этот квадрат разрезать на десять попарно различных клетчатых многоугольников?
б) Можно ли этот квадрат разрезать на одиннадцать попарно различных клетчатых многоугольников?
в) На какое наибольшее число попарно различных клетчатых прямоугольников можно разрезать этот квадрат?
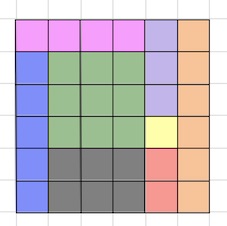
а) Да. Например, так:
б) Нет.
Различных одноклеточных многоугольников – 1.
Различных двуклеточных многоугольников – 1.
Различных трехклеточных многоугольников – 2.
Различных четырехклеточных многоугольников – 5.
Различных пытиклеточных многоугольников – более 5.
Даже если мы замостим квадрат 6х6 всеми 1,2,3,4-клеточными различными многоугольниками, то у нас останется всего 36-(1х1+1х2+2х3+5х4)=7 клеток. А нам придется разместить в них еще два многоугольника, отличных от ранее использованных, что невозможно.
в) Нас интересует наибольшее число попарно различных клетчатых прямоугольников, на которые можно разрезать данный квадрат. Значит, нам интересны из всех прямоугольников те, что занимают как можно меньшее количество клеток.
Покажем, что нельзя разместить 9 попарно различных клетчатых прямоугольников в данном квадрате.
Даже если мы разместим 8 различных прямоугольников, один из которых – 1-клеточный, один 2-двуклеточный, один 3-клеточный, два 4-клеточных, один 5-клеточный, два 6-клеточных прямоугольника, – на это у нас уйдет 31 клетка. В оставшихся 5 клетках следует разместить прямоугольник, ранее не упоминавшийся, что невозможно.
Покажем, что можно разместить 8 попарно различных клетчатых прямоугольников в данном квадрате. Например, так:
Ответ: а) да; б) нет; в) 8.
Теория для 19 задания ЕГЭ
Цифры и числа – это не синонимы. Цифры – это символы, которыми записывают числа. Числа состоят из цифр, как слова состоят из букв. Пример: число \(1806\) состоит из цифр \(1\), \(8\), \(0\) и \(6\).
Однозначные числа – числа, состоящие из одной цифры, например \(7\). Двухзначные числа – состоящие из двух цифр, например \(29\). Трехзначные – из трёх, например \(341\). И так далее.
Простое число – число, имеющее только два делителя, – единицу и само себя (при этом число \(1\) простым не считается). Пример: \(13\) или \(277\).
Составное число – число, имеющее больше двух делителей. Например, \(12\) или \(735\).
Натуральное число – целое положительное число. Пример: \(5\), \(34\), \(6908\)…
\(0\) – не натуральное, \(-7\) – тоже.
Четное число – целое число делящиеся на \(2\). Нечетное число – целое число не делящиеся на \(2\). Пример: \(12\), \(1000\), \(106\) – четные; \(3\), \(99\), \(9000001\) – нечетные.
Если написано «попарно различные числа», это означает, что все числа в наборе разные. То есть, любые \(2\) числа не равны друг другу. (Для меня загадка, почему в задачах не пишут просто «все числа разные»).
Если цифры числа неизвестны, их можно записать буквами и провести сверху черточку. Пример: \(\overline
Любое двухзначное число можно представить как: \(\overline
Трехзначное: \(\overline
Четырехзначное: \(\overline
\(n\) – значное: \(\underbrace<\overline
На \(2\): последняя цифра числа делится на \(2\) (в том числе \(0\))
На \(3\): сумма цифр числа делится на \(3\). Например, число \(4635\) делится на \(3\), т.к. \(4+6+3+5=18\) (а \(18\) делится на \(3\))
На \(4\): две последние цифры либо нули, либо образуют число, делящееся на \(4\)
На \(5\): последняя цифра \(0\) или \(5\)
На \(6\): одновременно соблюдаются признаки делимости на \(2\) и \(3\)
На \(7\): признаков делимости, увы, нет
На \(8\): три последние цифры нули или образуют число, делящееся на \(8\)
На \(9\): сумма цифр числа делится на \(9\)
На \(11\): разность между суммой цифр, стоящих на нечетных местах, и суммой цифр, стоящих на четных местах, делится на \(11\).
Например, число \(281765\) делится на \(11\), т.к. сумма цифр нечетных мест \(2+1+6=9\), сумма цифр на четных \(8+7+5=20\), т.е. разность между ними \(11\), а \(11\) делится на \(11\)
Если разность равна нулю – число тоже будет делиться на \(11\). Пример: число \(5247\).
На \(25\): две последнее цифры \(00\), \(25\), \(50\) или \(75\)
На \(100\): две последнее цифры \(00\)
На \(125\): три последнее цифры \(000\) или образуют число, делящееся на \(125\).
Число \(b\) делится на число \(a\), если найдётся такое целое число \(q\), что \(b=a \cdot q\).
Обозначается \(b \,\vdots \, a\). Например, \(6\) делится на \(2\), т.к. \(6=2\cdot 3\).
Также в этом случае число \(b\) называют кратным числу \(a\).
Общим делителем чисел называют такое число, которое является делителем для каждого из них. Например, общим делителем чисел \(12\) и \(30\) будет число \(4\).
Два числа называются взаимно простыми, если их общим делителем является только \(1\). Например: \(12\) и \(5\); \(25\) и \(14\); \(3\) и \(11\).
Замечание: два любых простых числа автоматически являются взаимно простыми.
Если одно из двух чисел делится на некоторое число, то и их произведение делится на это число. Например, \(9m\, \vdots \, 3\), так как \(9\) делится на \(3\) (здесь и далее \(m\), \(k\) и \(n\) – любые целые числа).
Если два числа делятся на некоторое число, то и их сумма, и их разность делятся на это число. Например, \((3k+9m)\, \vdots \, 3\), так как \(3k\) – делится на \(3\) и \(9m\) – делится на \(3\). Еще пример: \((99-88+77)\, \vdots \, 11\).
Если одно из чисел делится на некоторое число, а второе нет, то их сумма и их разность не делятся на это число. Например, если \(k\) целое, то: \((3k+17)\) 
\(3\); \((930-174)\) \(10\).
Если произведение нескольких чисел делится на некоторое простое число, то хотя бы одно из них делится на это простое число. Например, если \(5k\,⋮\,3\), то \(k\,⋮\,3\).
Каждое натуральное число, большее единицы, либо является простым, либо может быть разложено на простые множители.
Примеры:
число \(20\) может быть разложено в произведение \(2\cdot 2\cdot 5\)
число \(105 =21 \cdot 5=7\cdot 3 \cdot5\)
число \(17\) – является простым числом и разложено быть не может.
Замечание: разложение \(17\) как \(17\cdot 1\) – не подходит, т.к. единица не считается простым числом.
Любые два разложения одного и того же числа могут отличаться только порядком множителей.
Например, разложение числа \(6\) мы можем записать либо как \(2\cdot 3\), либо как \(3\cdot 2\) и более никак.
Замечание: вот именно поэтому \(1\) не считается простым числом, ведь иначе любое число имело бы бесконечно много разложений: \(2\cdot 3\cdot 1\); \(2\cdot 1\cdot 3\cdot 1\); \(2\cdot 1\cdot 3\cdot 1\cdot 1\cdot 1\)….
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Интересный вопрос
 |
Пусть дан некоторый фиксированный набор попарно различных КВАДРАТОВ P1. Pn
n-конечно ( Попарно различных означает что среди всех квадратов нет 2-х одинаковых)
Спрашивается:
1)Можно ли выложить из этих квадратов некоторый прямоугольник так что бы данные квадраты не пересекались и не находились один внутри другого.
2)Каково минимальное значение n при котором такое разложение возможно
3)Существует ли критерий позволяющий по данной системе прямоугольников за (разумное
время ) ответить на первый вопрос.
4)Для любого наперёд заданного прямоугольника ответить на вопрос «может ли он быть
разложен на какую нибудь систему попарно различных квадратов».
5)Для некоторого k ответить на вопрос « Существуют ли какие либо квадраты P1. Pk
Такие что из них можно выложить некоторый прямоугольник»?
| Заслуженный участник |
 |
По поводу разбиения прямоугольника на попарно различные квадраты посмотрите следующую книжечку:
И.М.Яглом, Как разрезать квадрат? «Наука», Москва, 1969.
Там же рассматривается и невозможность разбиения прямоугольного параллелепипеда на попарно различные кубы.
Что касается случая больших размерностей, то там такое разбиение тоже невозможно, причём, работает очень простое рассуждение: если бы существовало разбиение 
-мерного параллелепипеда на попарно различные -мерные кубы, то их следы на 
-мерных гранях параллелепипеда дают разбиения -мерных прямоугольников на попарно различные -мерные кубы. Если исходное разбиение содержало больше одного -мерного куба, то по меньшей мере на одной -мерной грани разбиение будет содержать больше одного -мерного куба.
|
Хотя стороны квадратов можно считать произвольными числами здесь рассматриваются
квадраты только с целыми сторонами.
На первые два вопроса существует точный ответ, а именно:
1)Например квадраты стороны которых относятся как 1:4:7:8:9:10:14:15:18
2)Минимальное количество квадратов из которых можно выложить прямоугольник равно 9.
Доказательство невозможности разложения произвольного паралелиппипеда на
систему попарно различных кубов так же существует. На остальные вопросы ответы (мне)
не извесны.
А основная гипотеза данной темы может быть сформулированна так:
Верно ли что: уравнение X^n+Y^n=Z^n имеет в целых числах решения тогда и только тогда
когда существует разложение некоторого n-мерного куба(паралелипипедда)
на систему попарно различных n-кубов?
| Заслуженный участник |
|
|
| Заслуженный участник |
|
Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
Что значит попарно различные прямоугольники
Дан клетчатый квадрат размером 6 × 6.
а) Можно ли этот квадрат разрезать на десять попарно различных клетчатых многоугольников?
б) Можно ли этот квадрат разрезать на одиннадцать попарно различных клетчатых многоугольников?
в) На какое наибольшее число попарно различных клетчатых прямоугольников можно разрезать этот квадрат?
а) Да, пример изображен на первом рисунке.
б) Нет. Есть один многоугольник площади 1, один многоугольник площади 2, два многоугольника площади 3, пять многоугольников площади 4. Поэтому 11 многоугольников требуют минимум
клеток.
в) Возьмем прямоугольники наименьшей площади. Их 1 для площади 1, 2, 3, 5 и 2 для площади 4 и 6. Эти 8 прямоугольников дают суммарную площадь
поэтому 9 прямоугольников взять нельзя. А 8 можно, пример изображен на втором рисунке.
Ответ: а) Да; б) Нет; в) 8.
