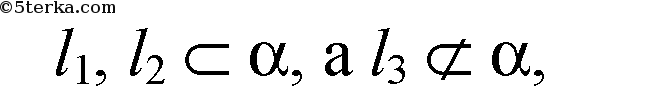Что значит попарно пересекаются
Сколько точек пересечения могут иметь четыре попарно пересекающиеся прямые?
Сразу говорю, что задачу решать НЕ НАДО. Оставьте это мне. Я просто хочу разобраться, что означает «попарное пересекающиеся прямые».
У меня есть такая интерпретация: Имеется в виду, что все прямые «собраны» в пары. И каждая такая «сладкая парочка» пересекается другой такой же парой или «одиночной» прямой. Правда в этом конкретном случае «одиночек» нет, ибо количество прямых четное.
Я правильно все понимаю, или моя интерпретация неверна? Если неверна, то что тогда имеется в виду?
задан 23 Май ’13 13:26
I_Robot
183 ● 4 ● 17 ● 38
92% принятых
Здесь имеется в виду, что какие бы две прямые из четырёх мы ни взяли, они будут пересекаться.
«они будут пересекаться.» Может быть, более точным будет сказать «они ДОЛЖНЫ пересекаться»?
Кстати, преобразуйте пожалуйста свой комментарий в ответ, дабы я мог закрыть вопрос.
3 ответа
Можно сказать «они пересекаются», «они должны пересекаться», «они будут пересекаться». Это всё одна и та же мысль. Суть в том, что любые две прямые из четырёх имеют точку пересечения. Фактически, это означает, что среди прямых нет параллельных (хотя в принципе такие прямые могли бы быть в какой-то другой ситуации, и тогда ответ был бы другим). Слово «попарно» вообще очень часто используется в математике. Например, «даны три попарно различных числа». Это значит, что первое число не равно второму, а также не равно третьему, а второе число не равно третьему.
отвечен 23 Май ’13 13:57
Если речь идет об одной паре прямых, то в одной точке, а ежели о двух парах и более, то рассматриваютя разные варианты расположения уже самих пересекающихся пар прямых.
отвечен 13 Сен ’15 13:02
Можете ли дать ссылку на определение «попарно пересекающиеся прямые» из учебника? Например как построить 5 попарно пересекающихся прямых? Можно-ли из этого сделать вывод, что одна прямая может пересекать лишь 2 других?
отвечен 22 Сен ’17 19:18
Здравствуйте
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №5. Взаимное расположение прямых в пространстве
Перечень вопросов, рассматриваемых в теме
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Два отрезка называются параллельными, если они лежат на паралельных прямых.
Открытый электронный ресурс:
Теоретический материал для самостоятельного изучения
Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)
Рисунок 1 – скрещивающиеся прямые
На прошлом уроке в качестве наглядного примера нами был приведен куб.
Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.
Примеры скрещивающихся прямых вокруг нас:
Одна дорога проходит по эстакаде, а другая под эстакадой
Горизонтальные линии крыши и вертикальные линии стен
Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.
Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).
Рисунок 2 – скрещивающиеся прямые АВ и СD
Итак, возможны три случая расположения прямых в пространстве:
Разберем и докажем еще одну теорему о скрещивающихся прямых.
Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)
1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.
Рисунок 3 – прямые АВ, СD, DЕ
Любая прямая, например ОО1, рассекает плоскость на две полуплоскости. Если лучи ОА и О1А1 параллельны и лежат в одной полуплоскости, то они называются сонаправленными.
Лучи О1А1 и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)
Рисунок 4 – сонаправленные лучи
Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)
Доказательство:
при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.
Отметим на сторонах угла O произвольные точки A и B.
На соответствующих сторонах угла O1 отложим отрезки OA1 и O₁B₁ равные соответственно ОA и OB.
2. В плоскости рассмотрим четырехугольник OAA1O1.
Так как противолежащие стороны OA и O1A1 этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA1 и OO1.
3. В плоскости, аналогично можно доказать, что OBB1O1 параллелограмм, поэтому равны и параллельны стороны ВВ1 и OO1.
4. Если две отрезка AA1 и BB1 равны параллельны третьему отрезку OO1, значит, они равны и параллельны, т. е. АА1||BB1 и AA1 = BB1.
По определению четырехугольник АВВ1А1 – параллелограмм и из этого получаем АВ=А1В1.
5.Из выше построенного и доказанного АВ=А1В1, ОA =O1A1 и OB =O1B1 следует, что треугольники AOB и A1 O1 B1. равны по трем сторонам, и поэтому О= О1.
Рисунок 5 – равные углы с сонаправленными сторонами
Про смартфон — цены, обзоры и реальные отзывы покупателей
На сайте Pro-Smartfon найдёте отзывы и обзоры топовых смартфонов 2017 года. Всё о плюсах и минусах мобильных телефонов. Свежие фотографии, цены и реальные отзывы покупателей о лучших смартфонах
Что значит попарно пересекаются
Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №15
к главе «Введение».
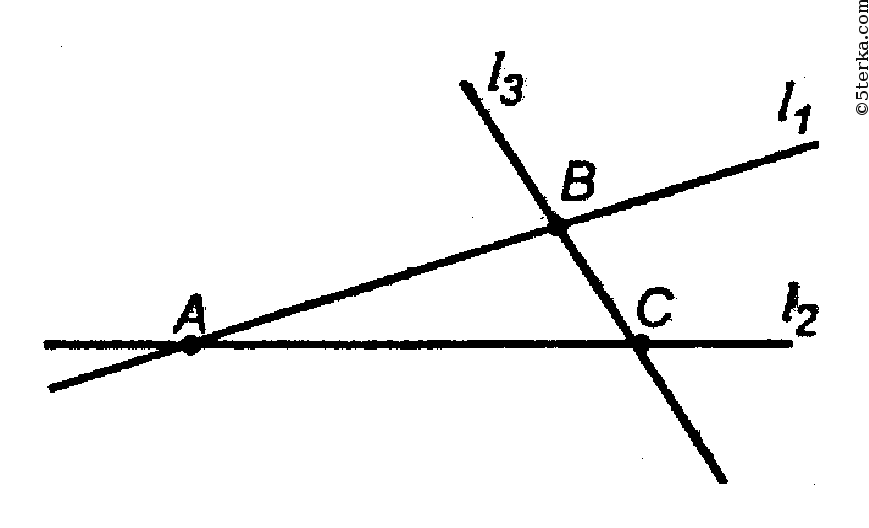
Каждая из трех точек принадлежит одновременно прямым.
Через три точки по аксиоме А1 можно провести единственную плоскость α. Поэтому отрезки АВ,
ВС и АС лежат в плоскость α
(по аксиоме А2), значит, прямые, которым принадлежат эти отрезки, тоже лежат в α.
Рассмотрим второй случай:
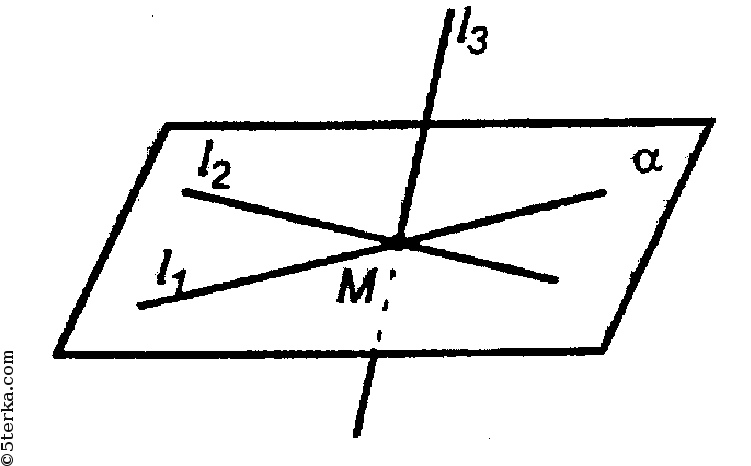
но и пересекается с l2 и l1 в точке М.
То есть прямые имеют общую точку, но не лежат в одной плоскости.
ПОПА́РНО, нареч. По двое, парами. Лебеди прилетают почти всегда попарно. С. Аксаков, Записки ружейного охотника. [Солдаты] стояли попарно, в полной караульной форме. Катаев, Белеет парус одинокий.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ПОПА’РНО, нареч. По-двое, парами. Ученики шли п.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
попарно
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова сонливый (прилагательное):
Синонимы к слову «попарно»
Предложения со словом «попарно»
Цитаты из русской классики со словом «попарно»
Понятия, связанные со словом «попарно»
Отправить комментарий
Дополнительно
Предложения со словом «попарно»:
Мы проследим эту фазу до следующей ступени развития, когда, под влиянием крепостного права, община примет ещё новую форму: это уже будет самоуправление каторги, коллективизм цепи, сковывающий людей попарно.
После этого стойки попарно перекрещивают между собой, а чтобы удержать их в таком состоянии, скрепляют места пересечения скрепкой.
Тотчас за телом шли двенадцать пар лилипутов, держась попарно за руки, одетые в чёрные кафтаны, с длинными, волочившимися по земле мантиями, обшитыми флёром.
Можете ли дать ссылку на определение «попарно пересекающиеся прямые» из учебника? Например как построить 5 попарно пересекающихся прямых, сколько точек пересечения у них может быть? Можно-ли из этого сделать вывод, что одна прямая может пересекать лишь 2 других?
задан 22 Сен ’17 19:30
2 ответа
Каждая из 5-ти прямых должна пересечь остальные 4 прямые. Нужную конфигурацию образуют, например, продолжения сторон правильного 5-угольника.
отвечен 22 Сен ’17 19:35
@Анатолий75: это чисто языковой оборот. Имеется в виду, что любая пара прямых пересекается (то есть среди них нет параллельных). Вопрос о том, сколько точек пересечения при этом может образоваться, требует разбора случаев.
Если все 5 прямых проходят через одну точку, то точка пересечения одна. Если нет тройных и более точек пересечения, то ответом будет 5*4/2=10 точек пересечения. Если 4 прямые проходят через одну точку, а пятая их отдельно пересекает, то точек получается 5. Если есть ровно одна тройная точка пересечения, то всего точек получится 8. Наконец, могут быть две тройные точки пересечения, и тогда точек 6.
Итого имеем 1, 5, 6, 8 или 10 точек пересечения.