Что значит подмножество чисел
Множества,их элементы,поджмножества
Вы будете перенаправлены на Автор24
В математике совокупности объектов, объединяющие ряд объектов называют множество. Данное понятие является первичным, значит, к более простым понятиям оно не сводится.
Термин множество употребляется тогда, когда речь идет о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек на координатной прямой, о множестве прямых, проходящих через точку.
Виды множеств
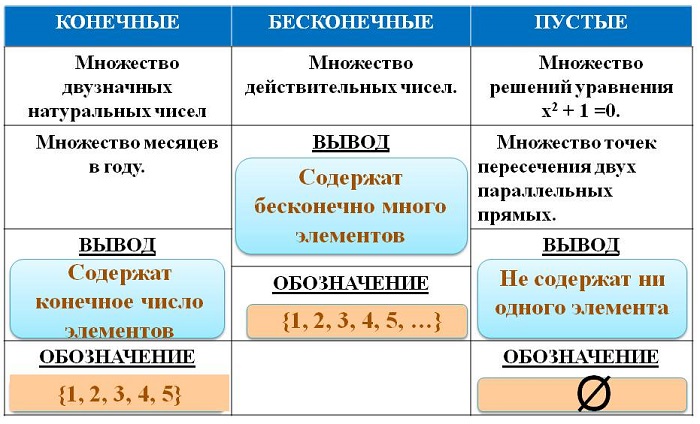
Множества могут быть конечными и бесконечными, пустыми.
Конечным называют множество, состоящее из конечного числа элементов, но при этом конечное множество может иметь любое количество элементов.
Среди конечных множеств выделяют множество, не имеющее ни одного элемента. Такое множество называется пустым множеством.
Множество, не являющееся конечным, называют бесконечным множеством.
Подмножества
Если некоторое множество не является пустым, то из него можно выделить другие множества, которые будут являться его частями.
Например, из множества натуральных чисел можно выделить множество четных.
Обозначение множеств, подмножеств и их элементов
Готовые работы на аналогичную тему
\[38\notin А, 74\notin А,934\notin А ; 12\in A,\ <\rm :\ >54\in A.\]
Способы задания множеств
Существует два глобально различных способа задания множеств.
Первый заключается в том, что множество задается указанием всех его элементов. В таком случае говорят, что множество задано перечислением всех своих элементов или списком своих элементов. Перечислением элементов можно задать только конечные множества и при небольшом количестве элементов, входящих в него
При таком способе задания множеств говорят, что множество задано перечислением его элементов.
Равенство множеств
Множества равны в том случае, если равны их элементы. При этом если множества состоят из одних и тех же элементов, но записанных в разном порядке то эти множества различны, хотя и равны.
Например, рассмотрим множества
Эти множества будут, состоят из равных элементов, значит, они будут равны, но при этом элементы расположены в разном порядке, т.е. множества различны
Пересечение множеств
Если даны два множества, то можно образовать новое множество, составленное из общих элементов этих множеств.
Например, рассмотрим два множества:
Объединение множеств
Математически это можно обозначить так:$\ А\ \cup B$
Разность множеств
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 27 05 2021
§1. Множества и операции над ними
Объяснение и обоснование
В курсах алгебры и алгебры и начал математического анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.
Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество М состоит из чисел 1; 2; 3, то его обозначают так: М = <1; 2; 3>. Тот факт, что число 2 входит в это множество (является элементом данного множества М), записывается с помощью специального значка ∈ следующим образом: 2 ∈ М; а то, что число 5 не входит в это множество (не является элементом данного множества), записывается так: 5 ∉ М.
Можно рассматривать также множество, не содержащее ни одного элемента, — пустое множество.
Например: множество простых делителей числа 1 — пустое множество.
Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом ∅, множество всех натуральных чисел — буквой N, множество всех целых чисел — буквой Z, множество всех рациональных чисел — буквой Q, а множество всех действительных чисел — буквой R.
Множества бывают конечными и бесконечными в зависимости от того, какое количество элементов они содержат. Так, множества А = <7>и M = <1; 2; 3>— конечные, потому что содержат конечное число элементов, а множества N, Z, Q, R — бесконечные.
Множества задают или с помощью перечисления их элементов (это можно сделать только для конечных множеств), или с помощью описания, когда задается правило (характеристическое свойство), которое позволяет определить, принадлежит или нет данный объект рассматриваемому множеству. Например, А = <–1; 0; 1>(множество задано перечислением элементов), B — множество всех четных целых чисел (множество задано характеристическим свойством всех элементов множества). Последнее множество иногда записывают так: B = или так: B =
В общем виде запись множества с помощью характеристического свойства можно обозначить так: A =
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества.
Из приведенного определения равенства множеств следует, что в множестве одинаковые элементы не различаются. Действительно, например, <1; 2; 2>= <1; 2>, поскольку каждый элемент первого множества (1 или 2) является элементом второго множества и, наоборот, каждый элемент второго множества (1 или 2) является элементом первого. Поэтому, записывая множество, чаще всего каждый его элемент записывают только один раз.
Если каждый элемент множества A является элементом множества B, то говорят, что множество A является подмножеством множества B.
Это записывают следующим образом: A ⊂ B.
Например, <1; 2>⊂ <0; 1; 2; 3>, N ⊂ Z (поскольку любое натуральное число — целое), Z ⊂ Q (поскольку любое целое число — рациональное), Q ⊂ R (поскольку любое рациональное число — действительное).
Полагают, что всегда ∅ ⊆ A, то есть пустое множество является подмножеством любого множества.
Иногда вместо записи A ⊂ B используется также запись A ⊆ B.
Сопоставим определение равенства множеств с определением подмножества. Если множества А и В равны, то: 1) каждый элемент множества А является элементом множества В, следовательно, А — подмножество В (A ⊆ B); 2) каждый элемент множества В является элементом множества А, следовательно, В — подмножество А (B ⊆ A). Таким образом,
два множества равны тогда и только тогда, когда каждое из них является подмножеством другого.
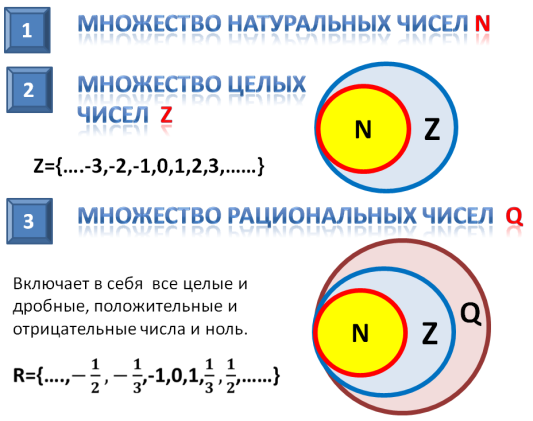
Иногда соотношения между множествами удобно иллюстрировать с помощью кругов (которые часто называют кругами Эйлера–Венна). Например, рисунок 1 иллюстрирует определение подмножества, а рисунок 2 — отношения между множествами N, Z, Q, R.
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.
Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками < >.
А = <а, в, с, у>– А состоит из четырех элементов.
Записать совокупность Z согласных букв в слове «калькулятор»:
Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N =
Выделяют три вида множеств:
пустые (обозначаются Ø) – не имеющие элементов.
Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
Множество натуральных чисел
Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.
Множество целых чисел
Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:
Множество рациональных чисел
Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:
Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:
Следовательно, N и Z являются подмножествами Q.
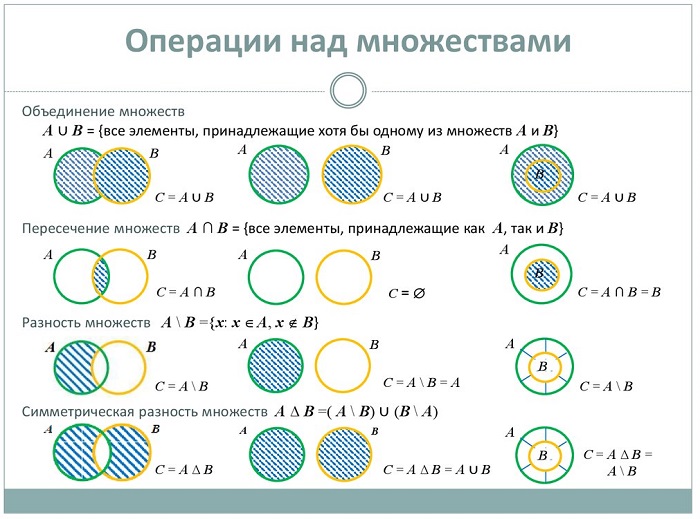
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:
Объединение
Пересечение
Дополнение
С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Свойства операций над множествами
Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:
Коммутативность – переместительные законы:
умножения S ∩ D = D ∩ S;
сложения S ∪ D = D ∪ S.
Ассоциативность – сочетательные законы:
умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).
Дистрибутивность – законы распределения:
умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).
если S ⊆ Fи F ⊆ J, то S ⊆ J;
если S ⊆ F и F ⊆ S, то S = F.
Идемпотентность объединения и пересечения:
О других свойствах операций можно узнать из картинки:
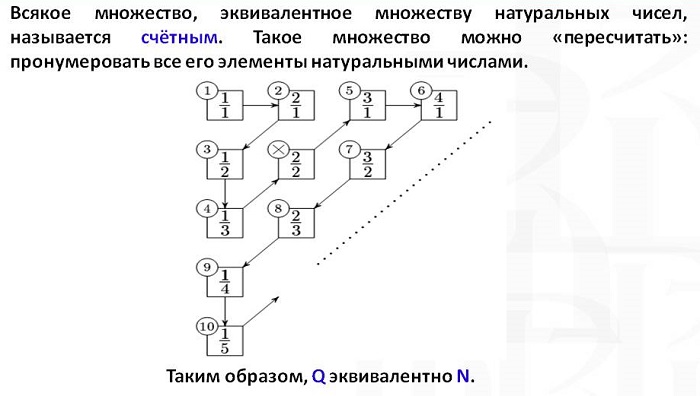
Счетные и несчетные множества
Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.
Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.
Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.
Словари
Под множеством понимается совокупность каких-либо объектов, называемых элементами множества. Теория множеств занимается изучением свойств как произвольных множеств, так и множеств специального вида независимо от природы образующих их элементов. Терминология и многие результаты этой теории широко используются в математике, например в математическом анализе, геометрии и теории вероятностей.
Сравнение множеств. Если из элементов двух множеств можно составить пары таким образом, чтобы каждому элементу первого множества соответствовал определенный элемент второго множества, а каждому элементу второго множества соответствовал один и только один элемент первого множества, то говорят, что между такими двумя множествами установлено взаимно однозначное соответствие. Чтобы установить взаимно однозначное соответствие, необязательно пересчитывать элементы множеств. Например, мы знаем, что американские штаты находятся во взаимно однозначном соответствии с их столицами, хотя можем оставаться в неведении относительно общего их числа. Мы могли бы утверждать: «Столиц штатов ровно столько, сколько штатов». Между двумя конечными множествами можно установить взаимно однозначное соответствие тогда и только тогда, когда оба множества состоят из одного и того же числа элементов. В теории множеств аналогичные утверждения используются, даже когда множества содержат бесконечно много элементов. Если между двумя множествами можно установить взаимно однозначное соответствие, то говорят, что они имеют одинаковое количество элементов или равномощны. Если же при любом способе образования пар некоторые элементы из первого множества остаются без пары, то говорят, что первое множество содержит больше элементов, чем второе, или, что первое множество имеет большую мощность. С понятием мощности связаны, казалось бы, удивительные результаты. Например, на первый взгляд положительных целых чисел в два раза больше, чем четных положительных чисел, так как четно каждое второе число. Но, согласно теории множеств, четных положительных чисел столько же, сколько всех положительных целых чисел. Действительно, можно образовать пары чисел 2 и 1, 4 и 2, 6 и 3 и, вообще каждому четному числу 2n поставить в соответствие целое число n. Именно это обстоятельство имел в виду Б. Рассел (1872-1970), сформулировав факт, названный им парадоксом Тристрама Шенди. Герой романа Стерна сетовал на то, что ему потребовался целый год, чтобы изложить события первого дня его жизни, еще один год понадобился, чтобы описать второй день, и что при таком темпе он никогда не завершит свое жизнеописание. Рассел возразил, заметив, что если бы Тристрам Шенди жил вечно, то смог бы закончить свое жизнеописание, так как события n-го дня Шенди мог бы описать за n-й год и, таким образом, в летописи его жизни ни один день не остался бы не запечатленным. Иначе говоря, если бы жизнь длилась бесконечно, то она насчитывала бы столько же лет, сколько дней. Эти примеры показывают, что бесконечное множество можно поставить во взаимно однозначное соответствие со своим бесконечным подмножеством. Иногда это свойство принимают за определение бесконечного. Если можно установить взаимно однозначное соответствие между некоторым множеством и множеством положительных целых чисел, то говорят, что такое множество счетно. Для обозначения количества элементов в счетном множестве часто используют символ А0 (алеф-нуль). Так называемые «трансфинитные» числа, например А0, могут не подчиняться обычным законам арифметики. Например, так как существует А0 четных чисел, А0 нечетных и А0 целых чисел, то приходится признать, что А0 + А0 = А0. Идея сравнения множеств путем установления взаимно однозначного соответствия между ними используется в различных разделах математики. Число всех действительных чисел, как показал основатель научной теории множеств Г. Кантор (1845-1918), больше, чем А0 чисел. Следовательно, если можно показать, что множество действительных чисел, обладающих некоторым особым свойством, является всего лишь счетным множеством, то заведомо должны существовать действительные числа, этим свойством не обладающие. Например, так как множество алгебраических чисел счетно, должны существовать неалгебраические числа. Такие числа называются трансцендентными. Поразительная и далеко не очевидная теорема, высказанная в качестве гипотезы Кантором и доказанная Э. Шредером и Ф. Бернштейном около 1896, утверждает, что если можно установить взаимно однозначное соответствие между множеством A и подмножеством множества B, и между множеством B и подмножеством множества A, то существует взаимно однозначное соответствие между всем множеством A и всем множеством B.
Аксиома выбора. Неожиданные трудности в теории множеств могут возникнуть, казалось бы, в самых простых случаях. Если, например, задано семейство непересекающихся множеств, ни одно из которых не пусто, то интуитивно кажется очевидным, что мы можем построить новое множество, содержащее ровно по одному элементу из каждого множества, входящего в это семейство. Но если наше семейство содержит бесконечно много множеств, то для построения нового множества может потребоваться бесконечное число произвольных выборов, а законность такого процесса при тщательном анализе становится отнюдь не очевидной. Аксиома выбора, утверждающая, что такое множество существует, была впервые сформулирована в 1904 Э. Цермело (1871-1953). До сих пор не удалось показать, что аксиома выбора следует из остальных аксиом теории множеств. Но около 1938 К.Гедель (1906-1978) показал, что если теория множеств непротиворечива (т.е. не содержит внутренних противоречий) без аксиомы выбора, то она остается непротиворечивой и после присоединения к ней аксиомы выбора.
Куратовский К., Мостовский А. Теория множеств. М., 1970
Что такое множество 👨🎓. Свойства и операции над множествами
В этой статье рассмотрим очень важную тему, как в математике, так и в информатике – множества. Ниже Вы найдете основные определения и понятия, свойства множеств, их виды и примеры. Материал изложен таким образом, что разберется даже полный чайник. Здесь приведены, только основы, которые обычно проходятся в рамках школьной программы. Читайте!
Основные положения и обозначения
Теория множеств появилась благодаря знаменитому немецкому математику Гео́рг Ка́нтор (3 марта 1845, Санкт-Петербург — 6 января 1918, Галле (Заале)) — немецкий математик, ученик Вейерштрасса. Наиболее известен как создатель теории множеств.
Итак, начнем с основных понятий. Основное определение имеет следующий вид:
Множества (м-ва – сокр.) – наборы элементов объединенных по какому либо признаку.
Обозначаются они с помощью заглавных латинских букв, а их элементы указываются в фигурных скобках.
Примеры
\( S = \left\ < а, б, в, г, д, …, ю, я \right\>\) – мн-во букв русского алфавита.
\( S = \left\ < Алексей, Анатолий, Галина, …, Александр, Ирина \right\>\) – мн-во имен студентов в группе.
\( S = \left\ < 🐵, 🙈, 🙉, 🙊 \right\>\) – мн-во смайликов с изображением обезьянок.
Также стоит обговорить про принадлежность элементов к множеству. Записать её можно с помощью специального значка «принадлежности» – \( \in \) . Так запись вида \( x \in S \) обозначает, что элемент x принадлежит множеству S.
С основным понятием разобрались, перейдем к остальной теории.
Подмножества
Подмножество – множество S1 является подмножеством S, если каждый элемент из S1 содержится (включен) в S.
Обозначают подмножества при помощи специального значка «включения», который имеет вид \( \subset \) \( (\ S_1 \subset S \ ) \) . Также их можно отобразить схематично, используя диаграммы Эйлера, которые отображают отношения между подмножествами.
Также Вы можете выделить подмножество мужских имен, или сделать любую выборку по какому-нибудь признаку.
Мощность
Следует также выделить такое понятие, как мощность. Имеет оно следующий вид:
Мощность – количество элементов, которое содержится в множестве.
Мн-ва называются равномощными тогда и только тогда, когда количество элементов одного из них равно количеству элементов другого.
Причем неважно, какие элементы будут в этих мн-ах. Так в одном из них могут содержаться 26 букв английского алфавита, а в другом 26 марок японских автомобилей, при этом они будут равномощными.
Мощность является одним из тех свойств, благодаря которому мы можем проводить сравнение двух (или более) м-в.
Равенство
Необходимо сказать и про равенство. Для чайников правило будет выглядеть так:
Два (или несколько) множеств равны только тогда, когда равны все их элементы.
Теперь изучим виды и другие свойства мн-в в математике.
Существует много критериев и свойств, по которым мы можем классифицировать множества. Например, мы можем разделить их по количеству элементов:
А можем поделить их на конечные (ограниченные) и бесконечные:
Теперь рассмотрим примеры множеств в математике.
Примеры
Натуральные числа
Натуральные числа в математике – это те числа, которые мы используем при счете (1, 2, 3 и т.д.). Сюда не относятся отрицательные величины и нуль. Запись: \( N = \left\ < 1, 2, 3, 4, 5, … \right\>\).
Целые числа
Получаются из множества натуральных чисел. К ним добавляются отрицательные числа и нуль. \( Z = \left\ < 0, \pm 1, \pm 2, \pm 3, \pm 4, \pm 5, … \right\>\).
Рациональные числа
Здесь множество задается следующим образом: \( Q = \left\ <
Так как любое число в математике можно представить в виде дроби (например, \( 5 = <5 \over 1>\) ), то целые числа являются подмножеством рациональных чисел. Натуральные же числа являются подмножеством целых чисел.
\[ N \subset Z \subset Q \]
Эту теорию Вам надо запомнить.
Операции
В этом разделе рассмотрим основные операции (действия) над множествами в математике.
Пересечение
Чтобы поняли даже чайники, вернемся к нашим «мартышкам»:
\( S_ <1>= \left\ < 🙉, 🙊 \right\>\) — обезьянки показывающие лапки и глаза
\( S_ <2>= \left\ < 🙈, 🙉 \right\>\) — мартышки показывающие лапы и рот
Надо найти \( S_ <1>\ \cap \ S_ <2>\). Для этого воспользуемся диаграммами Эйлера — Венна:
Решение: \( S_ <1>\ \cap \ S_ <2>= \left\ < 🙉 \right\>\) т.к. 🙉 входит и в S1 и в S2.
Объединение
Решение: \( S_ <1>\ \cup \ S_ <2>= \left\ < 🙈, 🙉, 🙊 \right\>\)
Разность
Решение: \( S_ <1>\ \setminus \ S_ <2>= \left\ < 🙊 \right\>\)
Следует отметить, что здесь приведены не все операции. Например, не написано про симметрическую разность и законы Моргана. Их проходят в рамках высшей математики.
Заключение
Теперь Вы знаете, что такое мн-ва, знаете их свойства и какие операции над ними можно выполнять. Надеюсь я объяснил всю теорию так, что понял даже полный чайник. Если же у Вас возникли вопросы, то задавайте их в комментариях. Также на нашем сайте Вы можете прочитать другие статьи, например про представления чисел в компьютере. Рассказывается как выполнять с ними такие действия, как перемножение, получение суммы и деление.