Что значит первый байт управляющий

Презентация на тему «Метод RLE-кодирования» (11 класс)

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Пример задания: Упаковка информации методом RLE-кодирования состоит в следующем. Упакованная последовательность содержит управляющие байты, за каждым управляющим байтом следует один или несколько байтов данных. Если старший бит управляющего байта равен 1, то следующий за управляющим байт данных при распаковке нужно повторить столько раз, сколько записано в оставшихся 7 битах управляющего байта. Если же старший бит управляющего байта равен 0, то надо взять несколько следующих байтов данных без изменения. Сколько именно – записано в оставшихся 7 битах управляющего байта. Например, управляющий байт 10000111 говорит о том, что следующий за ним байт надо повторить 7 раз, а управляющий байт 00000100 – о том, что следующие за ним 4 байта надо взять без изменений. После кодирования методом RLE получилась следующая последовательность байтов (первый байт – управляющий): 10000011 10101010 00000010 10101111 11111111 10000101 10101010. Сколько байт будет содержать данная последовательность после распаковки? Впишите в бланк только число.

Решение: обратите внимание, что в этой задаче НЕ нужно распаковывать последовательность, а нужно просто определить ее длину проанализируем первый управляющий байт, 10000011; он начинается с 1 – это команда на повторение следующего символа; количество повторений записано в семи младших битах: 112 = 3 раза; значит, раскодирование первых двух байт дает 3 символа следующий управляющий байт – третий, 00000010; его старший бит 0 говорит о том, что следующие 102 = 2 символа повторяются 1 раз; получаем еще 2 символа следующий управляющий байт – шестой, 10000101; он говорит о том, что следующий за ним символ нужно повторить 1012 =5 раз; получаем еще 5 символов полная длина распакованной последовательности равна 3 + 2 + 5 = 10 символов вот итог нашего анализа: Управляю-щий байты 1-3 Управляю-щий байт 4 байт 5 Управляю-щий байты 6-10 10000011 10101010 00000010 10101111 11111111 10000101 10101010

Упаковка информации методом RLE-кодирования состоит в следующем. Упакованная последовательность содержит управляющие байты, за каждым управляющим байтом следует один или несколько байтов данных. Если старший бит управляющего байта равен 1, то следующий за управляющим байт данных при распаковке нужно повторить столько раз, сколько записано в оставшихся 7 битах управляющего байта. Если же старший бит управляющего байта равен 0, то надо взять несколько следующих байтов данных без изменения. Сколько именно – записано в оставшихся 7 битах управляющего байта. Например, управляющий байт 10000111 говорит о том, что следующий за ним байт надо повторить 7 раз, а управляющий байт 00000100 – о том, что следующие за ним 4 байта надо взять без изменений. После кодирования методом RLE получилась следующая последовательность байтов (первый байт – управляющий): 00000011 10101010 00000010 10101111 10001111 11111111. Сколько байт будет содержать данная последовательность после распаковки? Впишите в бланк только число.

Источник

Содержание урока

Алгоритм RLE

Алгоритм RLE

При сжатии данных, в которых есть цепочки одинаковых кодов, можно применять ещё один простой алгоритм, который называется кодированием цепочек одинаковых символов (англ. RLE — Run Length Encoding). Представим себе файл, в котором записаны сначала 100 русских букв «А», а потом — 100 букв «Б»:

При использовании алгоритма RLE сначала записывается количество повторений первого символа, затем — сам первый символ, затем — количество повторений второго символа, затем — второй символ и т. д. В данном случае весь закодированный файл занимает 4 байта:

Таким образом, мы сжали файл в 50 раз за счёт того, что в нём снова была избыточность — цепочки одинаковых символов. Это сжатие без потерь, потому что, зная алгоритм упаковки, исходные данные можно точно восстановить из кода.

Очевидно, что такой подход будет приводить к увеличению (в 2 раза) объема данных в том случае, когда в файле нет соседних одинаковых символов. Чтобы улучшить результаты RLE-кодирования даже в этом наихудшем случае, алгоритм модифицировали следующим образом. Упакованная последовательность содержит управляющие байты, за каждым управляющим байтом следует один или несколько байтов данных. Если старший бит управляющего байта равен 1, то следующий за управляющим байт данных при распаковке нужно повторить столько раз, сколько записано в оставшихся 7 битах управляющего байта. Если же старший бит управляющего байта равен 0, то надо взять несколько следующих байтов данных без изменения. Сколько именно — записано в оставшихся 7 битах управляющего байта. Например, управляющий байт 10000111₂ говорит о том, что следующий за ним байт надо повторить 7 раз, а управляющий байт 00000100₂ — о том, что следующие за ним 4 байта надо взять без изменений. Например, последовательность

распаковывается в 17 символов: АААААААААААААААБВ.

Алгоритм RLE успешно использовался для сжатия рисунков, в которых большие области закрашены одним цветом, и некоторых звуковых данных. Сейчас вместо него применяют более совершенные, но более сложные методы. Один из них (алгоритм Хаффмана) мы рассмотрим далее. Алгоритм RLE используется, например, на одном из этапов кодирования рисунков в формате JPEG. Возможность использования RLE-сжатия есть также в формате BMP (для рисунков с палитрой 16 или 256 цветов).

Следующая страница Префиксные коды

Cкачать материалы урока

Источник

Алгоритм построения дерева

Пример: построить дерево Хаффмана и найти префиксные коды для сообщения: «КОЛ_ОКОЛО_КОЛОКОЛА»

· Составим таблицу частот вхождения символов

· Построим дерево Хаффмана

Блочное кодирование по методу Хаффмана формирует коды для буквосочетаний, составленных из m символов исходного алфавита.

Буквосочетания можно рассматривать как новый, расширенный алфавит объемом

N – объем исходного алфавита;

M – число символов в буквосочетании.

Блочное кодирование применяется к алфавитам, в которых вероятность появления одной какой-то буквы значительно превышает вероятность появления других букв.

Рассчитаем коэффициент сжатия сообщения.

Пример 3. Вычислили объем сообщения «КОЛ ОКОЛО КОЛОКОЛА» при использовании кодировок ASCII (Vascii =144 бита) и Unicode (Vunicode = 288 бит). Выше построили код Хаффмана для этой же фразы, на основании которого оценили объем сообщения Vхаффмана=39 бит.

В результате мы получаем коэффициент сжатия равный 144/39 = 3,7 для кодировки ASCII и 288/39 =7,4 для кодировки Unicode.

Метод RLE

В основу алгоритмов RLE (Run-Length Encoding – кодирование путем учета числа повторений) положен принцип выявления повторяющихся последовательностей данных и замены их простой структурой: повторяющийся фрагмент и коэффициент повторения.

Рассмотрим идею сжатия методом RLE. Во входной последовательности:

1. все повторяющиеся цепочки байтов заменяются на фрагменты <управляющий байт, повторяющийся байт>, причем управляющий байт в десятичной системе счисления должен иметь значение 128 + число повторений байта. Это означает, что старший бит управляющего байта для цепочки повторяющихся байтов всегда равен 1.

2. все неповторяющиеся цепочки байтов заменяются на фрагменты <управляющий байт, цепочка неповторяющихся байтов>, причем управляющий в десятичной системе счисления должен иметь значение 0+ длина цепочки. Это означат, что старший бит управляющего байта для цепочки неповторяющихся байтов всегда равен 0.

Замечание. В обоих случаях длина обрабатываем фрагмента не может превосходить 127 байт.

Пример 4. Упакуем методом RLE следующую последовательность из 14-ти байтов:

11111111 11111111 11111111 11111111 11111111 11110000 00001111 11000011 10101010 10101010 10101010 10101010 10101010 10101010

В начале последовательности 5 раз повторяется байт 11111111. Чтобы закодировать эти 5-ть байтов, запишем вначале управляющий байт 10000101, а затем сам повторяющийся байт 11111111. Рассмотрим как получился управляющийся байт: к значению 128 мы прибавили число повторений байта 5, получили 13310=100001012.

Далее идут 3 разных байта. Чтобы их закодировать, мы записываем управляющий байт 00000011 (112=310), а затем эти неповторяющиеся байты.

Далее в последовательности 7 раз идет байт 10101010. Чтобы закодировать эти 7 байтов, мы записываем управляющий байт 10000111 (128+7=13510=10001112), а затем повторяющийся байт 10101010.

В результате применения метода RLE мы получаем последовательность из 8-ми байтов: 10000101 11111111 00000011 11110000 00001111 11000011 10000111 10101010.

Таким образом, коэффициент сжатия 14/8=1,75.

1. Если во входной (сжатой) последовательности встречается управляющий байт с единицей в старшем бите, то следующий за ним байт данный надо записать в выходную последовательность столько раз, сколько указано в оставшихся 7-ми битах управляющего байта.

2. Если во входной (сжатой) последовательности управляющий байт с нулем в старшем бите, то в выходную последовательность нужно поместить столько следующих за управляющим байтов входной последовательности, сколько указано в оставшихся 7-ми битах управляющего байта.

Пример 5. Распакуем сжатую последовательность данных методом RLE:

00000010 00001111 11110000 10000110 11000011 00000011 00001111 00111100 01010101.

Первый байт данной последовательности управляющий 000000010, начинается с 0. Следовательно, следующие за ним 102=210 байта помещаются в выходную последовательность.

Замечание. Будем зачеркивать обработанные байты.

00000010 00001111 11110000 10000110 11000011 00000011 00001111 00111100 01010101

Следующий управляющий байт 10000110 начинается с 1. Следовательно, следующий за ним байт нужно поместить в выходную последовательность 1102=610 раз.

00000010 00001111 11110000 10000110 11000011 00000011 00001111 00111100 01010101

Следующий управляющий байт 00000011 начинается с 0. Следовательно, следующие за ним 112=310 байта нужно поместить в выходную последовательность.

Таким образом, все входные данные мы обработали. А распакованная последовательность байтов выглядит следующим образом:

00001111 11110000 11000011 11000011 11000011 11000011 11000011 11000011 00001111 00111100 01010101

Наилучшими объектами для данного алгоритма являются графические данные, в которых встречаются большие одноцветные участки. Различные реализации данного метода используются в графических форматах PCX, BMP и факсимильной передаче информации. Для текстовых данных данный метод неэффективен.

Источник

Алгоритмы обратимых методов.

Определение. Метод сжатия называется обратимым, если из данных, полученных при сжатии, можно точно восстановить исходный массив данных.

Обратимые методы можно применять для сжатия любых типов данных. Характерными форматами файлов, хранящих сжатую без потерь информацию, являются:

• GIF, TIF, PCX, PNG — для графических данных;

• AVI — для видеоданных;

• ZIP, ARJ, RAR, LZH, LH, CAB — для любых типов данных.

Существует достаточно много обратимых методов сжатия данных, однако в их основе лежит сравнительно небольшое количество теоретических алгоритмов, которые мы рассмотрим более подробно.

Суть метода упаковки заключается в уменьшении количества бит, отводимых для кодирования символов, если в сжимаемом массиве данных присутствует только небольшая часть используемого алфавита.

Пример. Входной текст «КОЛ_ОКОЛО_КОЛОКОЛА» содержит всего 5 различных символов («К», «О», «Л», «А» и «_»), следовательно, каждый символ может быть закодирован тремя битами. Всего в исходном тексте 18 символов, так что потребуется 18 × 3 = 54 бита. Округлив это значение с избытком до целого числа байт, получим размер сжатого массива — всего 7 байт. Коэффициент сжатия равен 18/7 = 2,(571428) ≈ 2,6.

Одно из преимуществ метода упаковки заключается в том, что любой фрагмент сжатых данных можно распаковать, совершенно не используя предшествующие данные. Действительно, зная номер требуемого символа N и длину кодов символов М, можно вычислить местоположение кода символа в сжатом массиве данных:

• номер байта, в котором начинается код символа, вычисляется так: L = [M-N/8];

• номер первого бита кода (в пределах этого байта) К равен остатку от деления M-N на 8.

Метод упаковки дает хорошие результаты, только если множество используемых символов невелико. Например, если в тексте используются только прописные русские буквы и знаки препинания, то текст может быть сжат всего на 25%: 33 русские буквы плюс пробел и знаки препинания — итого около 40 символов. Для их кодирования достаточно 6 бит. При упаковке текст уменьшится до 3/4 от первоначального объема.

Слабое место метода упаковки заключается в том, что символы кодируются битовыми последовательностями одинаковой длины. Например, любой текст, состоящий только из двух букв «А» и «В», сжимается методом упаковки в восемь раз. Однако если к такому тексту добавить всего лишь одну букву, например «С», то степень сжатия сразу уменьшится вдвое, причем независимо от длины текста и количества добавленных символов «С»!

Улучшения степени сжатия можно достичь, кодируя часто встречающиеся символы короткими кодами, а редко встречающиеся — более длинными. Именно такова идея метода, опубликованного Д. Хаффманом (Huffman) в 1952 г.

Идея кодирования символов кодами переменной длины была высказана и теоретически проработана амери­канскими учеными К. Шенноном и Р. М. Фано. Ими был предложен алгоритм построения эффективных сжимающих кодов переменной длины (алгоритм Шеннона—Фано), однако он в некоторых случаях строил неоптимальные коды. Алгоритм Хаффмана оказался простым, быстрым и оптимальным: среди алгоритмов, кодирующих каждый символ по отдельности и целым количеством бит, он обеспечивает наилучшее сжатие.

Алгоритм Хаффмана сжимает данные за два прохода: на первом проходе читаются все входные данные и подсчитываются частоты встречаемости всех символов. Затем по этим данным строится дерево кодирования Хаффмана, а по нему — коды символов. После этого, на втором проходе, входные данные читаются еще раз и при этом генерируется выходной массив данных.

Вычисление частот встречаемости — тривиальная задача. Разберем построение дерева кодирования Хаффмана.

Алгоритм построения дерева Хаффмана

1. Символы входного алфавита образуют список свободных узлов. Каждый узел имеет вес, равный количеству вхождений символа в исходное сообщение.

3. Создается их узел-«родитель» с весом, равным сумме их весов, он соединяется с «детьми» дугами.

4. Одной дуге, выходящей из «родителя», ставится в соответствие бит 1, другой — бит 0.

5. «Родитель» добавляется в список свободных узлов, а двое его «детей» удаляются из этого списка.

6. Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева

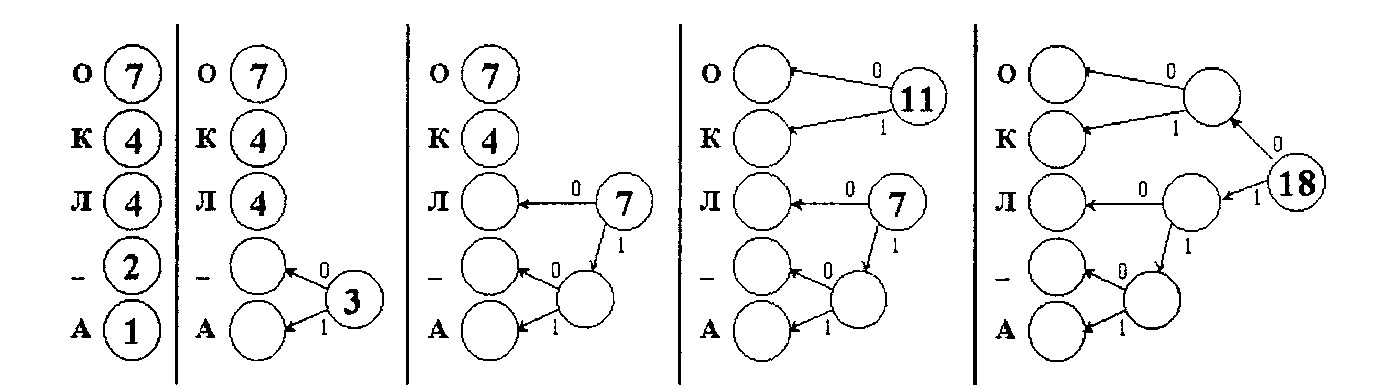
Пример. Построение дерева Хаффмана и префиксных кодов для текста «KOJI_OKOJIO_KOJIOKOJIA»:

Пусть у нас имеется список частот встречаемости всех символов исходного текста. Выпишем их вертикально в ряд в виде вершин будущего графа. Выберем две вершины с наименьшими весами (они соответствуют символам с наименьшим количеством повторений). Объединим эти вершины — создадим новую вершину, от которой проведем ребра к выбранным вершинам с наименьшими весами, а вес новой вершины зададим равным сумме их весов. Расставим на ребрах графа числа 0 и 1, например на каждом верхнем ребре 0, а на каждом нижнем — 1. Чтобы выбранные вершины более не просматривались, мы сотрем их веса (это аналог удаления вершин из списка). Продолжим выполнять объединение вершин, каждый раз выбирая пару вершин с наименьшими весами, до тех пор пока не останется одна вершина. Очевидно, что вес этой вершины будет равен длине сжимаемого массива данных.

Теперь для определения кода каждой конкретной буквы необходимо просто пройти от вершины дерева до этой буквы, выписывая нули и единицы по маршруту следования. В нашем примере символы получат следующие коды:

После того как коды символов построены, остается сгенерировать сжатый массив данных, для чего надо снова прочесть входные данные и каждый символ заменить на соответствующий код. В нашем случае непосредственно код текста будет занимать 39 бит, или 5 байт. Коэффициент сжатия равен 18/5 = 3,6. Для восстановления сжатых данных необходимо снова воспользоваться деревом Хаффмана, так как код каждого символа представляет собой путь в дереве Хаффмана от вершины до конечного узда дерева, соответствующего данному символу. Общая схема процесса восстановления такова: специальный маркер устанавливается в вершину дерева Хаффмана, и сжатый массив данных читается побитово. Если читаемый бит равен О, то маркер перемещается из вершины по верхнему ребру, если 1, то по нижнему. Затем читается следующий бит, и маркер снова перемещается, и т. д., пока маркер не попадет в один из конечных узлов дерева. В восстанавливаемый массив записывается символ, которому соответствует этот конечный узел, маркер снова помещается в вершину дерева, и процесс повторяется.

Код Хаффмана является префиксным. Это означает, что код каждого символа не является началом кода какого-либо другого символа. Код Хаффмана однозначно восстановим, даже если не сообщается длина кода каждого переданного символа.

В основу алгоритмов RLE (англ. Run-Length Encoding — кодирование путем учета числа повторений) положен принцип выявления повторяющихся последовательностей данных и замены их простой структурой: повторяющимся фрагментом и коэффициентом повторения.

Рассмотрим идею сжатия данных по методу RLE (это не метод, а идея):

Ограничения – длина обрабатываемого фрагмента не должна превосходить 127 байтов.

Пример. Надо упаковать методом RLE следующую последовательность

11111111 11111111 11111111 11111111 11111111

11110000 00001111 11000011 10101010 10101010

10000101 11111111 00000011 11110000 00001111

11000011 10000100 10101010

Таким образом, 12 байт упаковали в 8 байт, и значит, коэффициент сжатия равен 2/3, т.е. 66 процентов.

Различные реализации данного метода используются в графических файлах форматов PCX, BMP, при факсимильной передаче информации. Для текстовой информации метод RLE неэффективен.

Алгоритмы Лемпеля-Зива.

В конце 70-х годов прошлого века израильские ученые Яков Зив и Абрахам Лемпель предложили алгоритмы сжатия LZ77 и LZ78. Оригинальность алгоритмов состоит в том, что сжимаются здесь не только относительно буквы но и слова.

Общая схема алгоритма LZ77 такова (это не точное описание алгоритма):

• входные данные читаются последовательно, текущая позиция условно разбивает массив входных данных на прочитанную и непрочитанную части;

• для цепочки первых байтов непрочитанной части ищется наиболее длинное совпадение в прочитанной части. Если совпадение найдено, то составляется комбинация <смещение, длина>, где смещение указывает, на сколько байтов надо сместиться назад от текущей позиции, чтобы найти совпадение, а длина — это длина совпадения;

• если запись комбинации <смещение, длина>короче совпадения, то она записывается в выходной массив, а текущая позиция перемещается вперед (на длину совпадающей части);

• если совпадение не обнаружено или оно короче записи комбинации <смещение, длина>, то в выходной массив копируется текущий байт, текущая позиция перемещается вперед на 1, и анализ повторяется.

Пример. Фраза КОЛОКОЛ_ОКОЛО_КОЛОКОЛЬНИ зако- дируется алгоритмом LZ77 как КО ЛО(-4,3)_(- 5,4 )0_(-14,7)ЬНИ.

Общая схема алгоритма LZ78 такова (это не точное описание алгоритма):

• алгоритм во время сжатия текста создает специаль­ный словарь повторяющихся цепочек, в словаре каждой цепочке соответствует короткий код;

• для цепочки первых байтов непрочитанной части ищется наиболее длинное совпадение в словаре. Код совпадения записывается в выходной массив, туда же заносится первый несовпавший символ, и текущая позиция перемещается вперед на длину совпадения + 1;

• в словарь добавляется новое слово: «совпадение» + + «несовпавший символ», и процесс повторяется до тех пор, пока не будет сжат весь входной массив.

Источник

Тема Анализ алгоритма построения последовательности Что нужно знать

Тема: Анализ алгоритма построения последовательности.

в некоторых задачах (на RLE-кодирование, см. далее) нужно знать, что такое бит и байт, что байт равен 8 бит, что такое старший бит, как переводить числа из двоичной системы в десятичную

в классических задачах (на символьные цепочки) каких-либо особых знаний из курса информатики, кроме умения логически мыслить, не требуется

Пример задания:

Латинский алфавит (для справки): ABCDEFGHIJKLMNOPQRSTUVWXYZ

Запишите семь символов подряд, стоящие в восьмой строке со 126-го по 132-е место (считая слева направо).

используя приведенное правило, можно построить следующие строки:

(5) E DCBAABAACBAABAADCBAABAACBAABAA

(6) F E DCBAABAACBAABAADCBAABAACBAABAA E DCBAABAACBAABAADCBAA
BAACBAABAA

мы быстро убедимся, что следующие строки получаются достаточно длинные, и легко запутаться, отсчитывая символы с номерами 126-132 в восьмой строке

попробуем найти закономерности, позволяющие решить задачу без выписывания 8-ой строки;

восьмая строка строится так: восьмая буква латинского алфавита (H) и затем – два раза седьмая строка (сверху написаны номера символов)

символы 126-132 находятся на границе двух цепочек, повторяющих 7-ую строку; заметим, что в соответствии с заданным алгоритмом можно легко определить первые символы в 7-ой строке (GFEDC) и последние символы (AABAA)

далее сразу находим, что интересующая нас часть 8-ой строки имеет вид

таким образом, правильный ответ – BAAGFED.

Возможные ловушки и проблемы :

можно, конечно, попробовать выписать заданную строку и выделить нужные символы, но этот подход очень трудоемкий и чреват случайными ошибками

чаще всего заданная цепочка находится на границе, где соединяются две части строки (например, в этом задании – на границе двух последовательностей, совпадающих с 7-ой строкой)

в задачах этого типа часто встречается игра на последовательностях вида

полезно помнить формулу, которая «сворачивает» сумму степеней двойки:

Еще пример задания:

Упаковка информации методом RLE-кодирования состоит в следующем. Упакованная последовательность содержит управляющие байты, за каждым управляющим байтом следует один или несколько байтов данных. Если старший бит управляющего байта равен 1, то следующий за управляющим байт данных при распаковке нужно повторить столько раз, сколько записано в оставшихся 7 битах управляющего байта. Если же старший бит управляющего байта равен 0, то надо взять несколько следующих байтов данных без изменения. Сколько именно – записано в оставшихся 7 битах управляющего байта. Например, управляющий байт 10000111 говорит о том, что следующий за ним байт надо повторить 7 раз, а управляющий байт 00000100 – о том, что следующие за ним 4 байта надо взять без изменений.
После кодирования методом RLE получилась следующая последовательность байтов (первый байт – управляющий):

10000011 10101010 00000010 10101111 11111111 10000101 10101010.

Сколько байт будет содержать данная последовательность после распаковки? Впишите в бланк только число.

обратите внимание, что в этой задаче НЕ нужно распаковывать последовательность, а нужно просто определить ее длину

проанализируем первый управляющий байт, 1 0000011 ; он начинается с 1 – это команда на повторение следующего символа; количество повторений записано в семи младших битах: 11 2 = 3 раза; значит, раскодирование первых двух байт дает 3 символа

следующий управляющий байт – третий, 0 0000010 ; его старший бит 0 говорит о том, что следующие 10 2 = 2 символа повторяются 1 раз; получаем еще 2 символа

следующий управляющий байт – шестой, 1 0000101 ; он говорит о том, что следующий за ним символ нужно повторить 101 2 =5 раз; получаем еще 5 символов

полная длина распакованной последовательности равна 3 + 2 + 5 = 10 символов

Источник