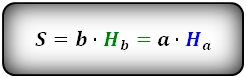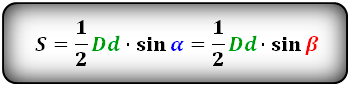Что значит перпендикулярно в геометрии в параллелограмме

Параллелограмм. Формулы, признаки и свойства параллелограмма

Рис.1	Рис.2

Признаки параллелограмма

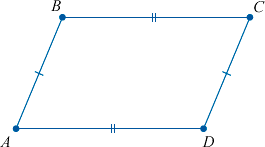
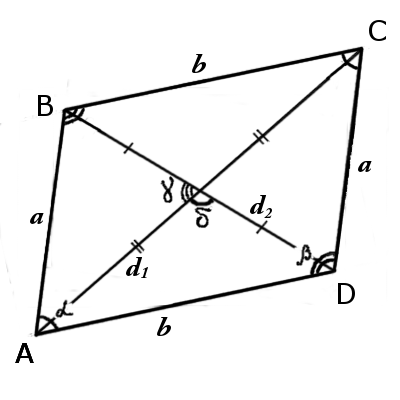
AB||CD, AB = CD (или BC||AD, BC = AD)

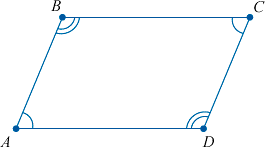
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2

Основные свойства параллелограмма

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

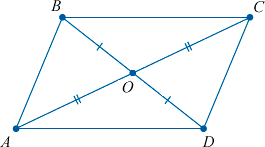
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:

AC 2 + BD 2 = 2AB 2 + 2BC 2

Стороны параллелограмма

Формулы определения длин сторон параллелограмма:

1. Формула сторон параллелограмма через диагонали и угол между ними:

2. Формула сторон параллелограмма через диагонали и другую сторону:

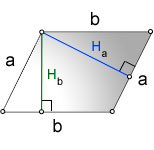
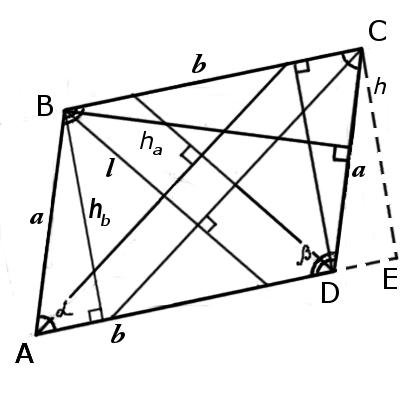
3. Формула сторон параллелограмма через высоту и синус угла:

4. Формула сторон параллелограмма через площадь и высоту:

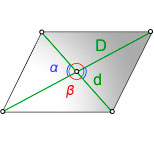
Диагонали параллелограмма

Формулы определения длины диагонали параллелограмма:

d ₂ = √ a 2 + b 2 + 2 ab·cosβ

d ₁ = √ a 2 + b 2 + 2 ab·cosα

4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:

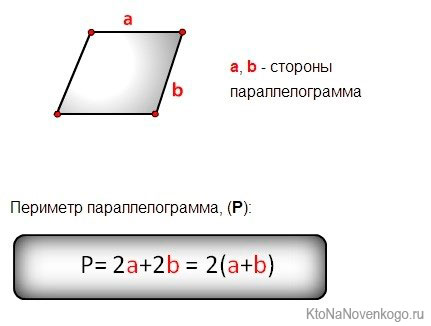
Периметр параллелограмма

Формулы определения длины периметра параллелограмма:

P = 2 a + 2 b = 2( a + b )

3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:

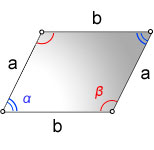
Площадь параллелограмма

Формулы определения площади параллелограмма:

3. Формула площади параллелограмма через две диагонали и синус угла между ними:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Параллелограмм

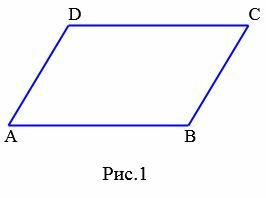
Определение 1. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.

Свойства параллелограмма

Свойство 1. В параллелограмме противоположные углы равны и противоположные стороны равны.

Доказательство. Рассмотрим параллелограмм ABCD (Рис.2).

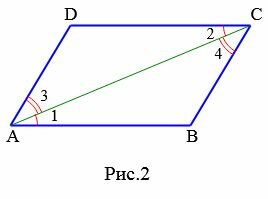Диагональ AC разделяют параллелограмм на два треугольника ACB и ACD. \( \small \angle 1=\angle 2 \) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC (см. теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично \( \small \angle 3=\angle 4 \), если рассмотреть параллельные прямые AD и BC пересеченные секущей AC. Тогда треугольники ACB и ACD равны по одной стороне и двум прилежащим углам: AC общая, \( \small \angle 1=\angle 2 \), \( \small \angle 3=\angle 4 \) (см. статью Треугольники. Признаки равенства треугольников). Поэтому \( \small AB=CD, \;\; AD=BC, \;\; \angle B=\angle D. \)

Из рисунка Рис.2 имеем: \( \small \angle A=\angle 1+\angle 3, \;\; \angle C=\angle 2+\angle 4. \) Учитывая, что \( \small \angle 1=\angle 2 \) и \( \small \angle 3=\angle 4 \), получим: \( \small \angle A=\angle C. \)

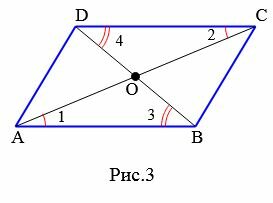
Свойство 2. Диагонали параллелограмма точкой пересечения разделяются пополам.

Доказательство. Рассмотрим параллелограмм ABCD (Рис.3) и пусть O точка пересечения диагоналей AC и BD. \( \small \angle 1=\angle 2 \) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC. \( \small \angle 3=\angle 4 \), если рассмотреть параллельные прямые AB и CD пересеченные секущей BD. Поскольку в параллелограмме противоположные стороны равны: AB=CD (Свойство 1), то треугольники ABO и CDO равны по стороне и прилежашим двум углам. Тогда AO=OC и BO=OD.

Признаки параллелограмма

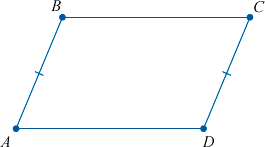
Признак 1. Если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник является параллелограммом.

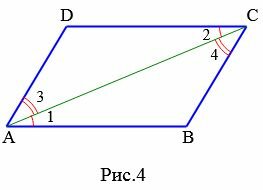Доказательство. Рассмотрим параллелограмм ABCD. Пусть AB=CD и AB || CD. Проведем диагональ AC (Рис.4). Поскольку AB || CD, то \( \small \angle 1=\angle 2 \) как накрест лежащие углы − при рассмотрении параллельных прямых AB и CD пересеченных секущей AC. Тогда треугольники ACB и ACD равны, по двум сторонам и углу между ними. Действительно, AB=CD, AC− общая сторона \( \small \angle 1=\angle 2 \). Но тогда \( \small \angle 3=\angle 4. \) Рассмотрим прямые AD и BC, пересеченные секущей AC. Поскольку \( \small \angle 3 \) и \( \small \angle 4 \) являются накрест лежашими углами, то по теореме 1 статьи Параллельные прямые. Признаки параллельности прямых, эти прямые параллельны. Таким образом, в четырехугольнике противоположные стороны попарно параллельны (AB || CD, AD || BC) и, значит, данный четырехугольник параллелограмм.

Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник является параллелограммом.

Доказательство. Рассмотрим параллелограмм ABCD (Рис.4). Проведем диагональ AC (Рис.4). Рассмотрим треугольники ACB и ACD. Эти треугольники равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Действительно. AC − общая для этих треугольников и по условию AB = CD, AD = BC. Тогда \( \small \angle 1=\angle 2 \). Отсюда следует AB || CD. Имеем, AB = CD, AB || CD и по признаку 1 четырехугольник ABCD является параллелограммом.

Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения разделяются пополам, то данный четырехугольник − параллелограмм.

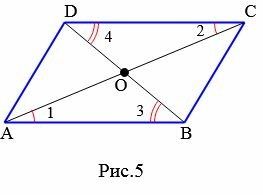Доказательство. Рассмотрим четырехугольник ABCD (Рис.5). Пусть диагонали четырехугольника пересекаются в точке O и точкой пересечения делятся пополам:

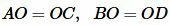Углы AOB и COD вертикальные, следовательно \( \small \angle AOB=\angle COD \). Тогда треугольники AOB и COD равны по двум сторонам и углу меду ними:

,

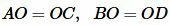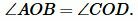Тогда AB = CD и \( \small \angle 1=\angle 2 \). Но по признаку параллельности прямых следует, что AB || CD (теорема 1 статьи Параллельные прямые. Признаки параллельности прямых). Получили:

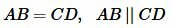и, по признаку 1 четырехугольник ABCD − параллелограмм.

Источник

Параллелограмм — это базовая геометрическая фигура с рядом важных свойств и признаков

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

В этой статье мы подробно расскажем о таком термине, как ПАРАЛЛЕЛОГРАММ.

С этой фигурой каждый из нас познакомился еще в школе – на уроках геометрии в 8 классе. Но если кто проболел в то время, прогулял занятия или просто не усвоил материал – мы поможем закрыть этот пробел.

Определение параллелограмма

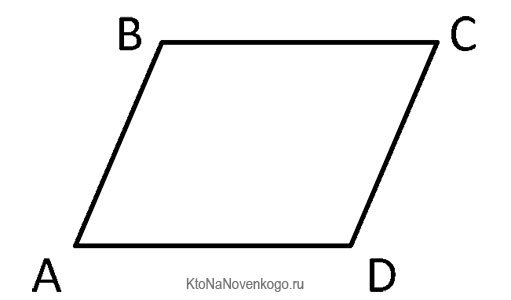
Параллелограмм – это геометрическая фигура, которая является разновидностью четырехугольника. У него противоположные стороны лежат на параллельных линиях, а соответственно, являются параллельными по отношению друг к другу.

Выглядит эта фигура вот так:

Это классический вид параллелограмма, который в учебниках приводят всегда в первую очередь. В данной фигуре сторона AD параллельна стороне ВС, а АВ параллельна CD.

Интересно, что более известные всем нам фигуры – квадрат, прямоугольник и ромб – также являются параллелограммами.

Можно даже дать такие определения:

Происхождение термина «параллелограмм»

Как и многие термины в математике, слово ПАРАЛЛЕЛОГРАММ пришло к нам из Древней Греции. И легко предположить, что оно как-то связано с самым известным в истории математиком – Евклидом.

Действительно, так и есть. Слово ПАРАЛЛЕЛОГРАММ впервые можно найти именно в трудах Эвклида, которые называются «Начала». Оно состоит из двух греческих слов – «Parallelos», что, естественно, означает «параллельный», и «Gramme» — «линия».

Таким образом, ПАРАЛЛЕЛОГРАММ можно перевести как «параллельные линии». Этот принцип и заложен в определении геометрической фигуры.

Еще любопытный факт, что именно Евклид поделил все четырехугольники на две большие категории. Первая – это параллелограммы, у которых противоположные стороны параллельны. И трапеции (что это?), у которых параллельна только одна пара сторон.

Свойства и признаки параллелограмма

Как понять, что перед нами ПАРАЛЛЕЛОГРАММ? Есть целый ряд признаков, который характерен только для этой геометрической фигуры.

Возьмем в качестве примера еще раз нашу фигуру:

Чтобы этот четырехугольник ABCD можно было считать параллелограммом, должно выполняться одно из следующих условий:

AD II BC и AD =BC. Или AB II CD и AB = CD

∠А + ∠В = ∠В + ∠С = ∠С + ∠D = ∠D + ∠А = 180

Это самые простые признаки параллелограмма. Есть еще некоторые признаки, смысл которых поясняется в этом видео:

Причем, для того чтобы удостовериться в подлинности фигуры, достаточно доказать только одно из них.

Правило действует и в обратную сторону – если хоть один из признаков параллелограмма верен, то автоматически верны и все остальные, и они не нуждаются в отдельном доказательстве.

Соответственно, если хоть один признак не получил подтверждения, то фигуру нельзя считать параллелограммом. И все остальное также не совпадет.

Как посчитать периметр параллелограмма

Для подсчетов длины периметра четырехугольников обычно просто складывают длины его сторон. Но в случае с параллелограммом все несколько проще, так как стороны у него попарно равны.

Снова возьмем для примера нашу фигуру:

Только для удобства обозначим стороны по-другому. AD и ВС будет просто «а», а АВ и CD – «b». Получится вот так:

Чтобы рассчитать периметр, надо просто сложить все стороны:

Но эту же формулу можно переиначить и по-другому:

Это и есть формула периметра параллелограмма, которая записана во всех учебниках.

Как рассчитать площадь параллелограмма

С площадью геометрических фигур всегда чуть сложнее, чем с периметрами. Но параллелограмм в какой-то мере уникален, потому что для расчета его площади существует сразу несколько формул.

Напомним, высотой называют линию, которая выходит из вершины геометрической фигуры и идет под прямым углом к противоположному основанию.

Вот и все, что мы хотели рассказать о ПАРАЛЛЕЛОГРАММЕ. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Сталкивалась с этим словом только в школе, на уроках геометрии, больше нигде 🙂

Источник

Параллелограмм — признаки и свойства

Клод Бернард однажды сказал:

«Думать, что всё знаешь, останавливает тебя от того, чтобы учиться новому»

Давай узнаем что-то новое сегодня, разбирая, казалось бы, такую простую тему!

Статья поможет тебе окончательно разобраться с самыми «популярными» параллелограммами, а наши вебинары дадут тебе необходимую практику.

И на ЕГЭ ты сможешь решить любую задачу на эту тему!

Параллелограмм — коротко о главном

Параллелограмм – четырехугольник, противоположные стороны которого попарно параллельны.

Свойства параллелограмма:

Прямоугольник – четырехугольник, все углы которого прямые: \( \displaystyle \angle A=\angle B=\angle C=\angle D=90<>^\circ \).

Свойства прямоугольника:

Ромб – четырехугольник, все стороны которого равны между собой: \( \displaystyle AB=BC=CD=DA\).

Свойства ромба:

Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые: \( \displaystyle AB=BC=CD=DA\); \( \displaystyle \angle A=\angle B=\angle C=\angle D=90<>^\circ \).

Свойства квадрата:

\( \displaystyle ABCD\) – ромб

Источник

Планиметрия. Страница 4

1.Параллелограмм

Теорема: если диагонали четырехугольника пересекаются и делятся этой точкой пересечения пополам, то такой четырехугольник называется параллелограммом.

Рис.1 Теорема. Параллелограмм.

Теорема. если четырехугольник является параллелограммом, то его диагонали делятся точкой пересечения пополам.

Доказательство. Пусть дан параллелограмм АВСD. (Рис. 2)

Тогда его стороны AD и BC равны и лежат на параллельных прямых а и b. Если мы проведем секущие с и d так, чтобы прямая с проходила через точку А и С, а прямая d проходила через точку B и D, то угол ОАD будет равен углу ОСВ, а угол ОDА будет равен углу ОВС, как внутренние накрест лежащие. Следовательно, треугольники АОD и ВОС равны по стороне и прилегающим к ней углам. А отсюда следует и равенство сторон этих треугольников. Т.е. АО = ОС, а ВО = ОD. Сумма этих сторон и есть диагонали параллелограмма.

Пример 1

Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что ее отрезок, заключенный между параллельными сторонами, делится этой точкой пополам. (Рис.9)

Доказательство:

Пусть ABCD данный параллелограмм. EF данный отрезок, проходящий через точку О пересечения диагоналей.

Рассмотрим треугольники COF и AOE. Сторона АО треугольника АОЕ равна стороне ОС треугольника COF по свойству параллелограмма. Угол при вершине А треугольника АОЕ равен углу при вершине С треугольника COF, как внутренние накрест лежащие углы. Углы при вершине О у обоих треугольников равны как вертикальные.

Отсюда можно сделать вывод, что треугольники АОЕ и COF равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Следовательно, отрезки OF и ОЕ равны.

Рис.9 Задача. Через точку пересечения диагоналей.

Пример 2

Две стороны параллелограмма относятся как 3:4, а его периметр равен 2,8 м. Найдите стороны параллелограмма. (Рис.10)

Решение:

Пусть ABCD данный параллелограмм. Обозначим сторону АВ как 3х, а сторону ВС как 4х. Тогда составим следующее соотношение:

Рис.10 Задача. Две стороны параллелограмма.

Пример 3

В параллелограмме ABCD перпендикуляр, опущенный из вершины В на сторону AD, делит ее пополам. Найдите диагональ BD и стороны параллелограмма, если периметр параллелограмма равен 4 м, а периметр треугольника ABD равен 3 м. (Рис.11)

Решение:

P_ABCD = 2*(х + 2y) = 4, P_ABD = 2x +2y = 3

Рис.11 Задача. В параллелограмме ABCD перпендикуляр.

Пример 4

В прямоугольный треугольник, каждый катет которого равен 8 см, вписан прямоугольник, имеющий с треугольником общий угол. Найдите периметр прямоугольника.(Рис.12)

Решение:

Отсюда следует, что FE = AD = 8-х, а BD = х.

Теперь можно составить следующее соотношение:

Периметр прямоугольника ADEF равен 16 см.

Рис.12 Задача. В прямоугольный треугольник.

Пример 5

Докажите, что если у параллелограмма диагонали перпендикулярны, то он является ромбом.(Рис.13)

Доказательство:

Отсюда следует, что эти треугольники равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Сторона АВ = DC и внутренние накрест лежащие углы при них равны. Следовательно, АО = ОС, а ВО = OD.

Теперь рассмотрим треугольники AOD и DOC. Они также равны, но по первому признаку равенства треугольников. Сторона АО = ОС, а сторона OD у них общая. Углы при вершине О равны 90°. Т.е. по двум сторонам и углу между ними.

Следовательно, можно сделать вывод, что сторона AD = DC = AB = BC, т.е. данный параллелограмм является ромбом.

Рис.13 Задача. Докажите, что если у параллелограмма.

Источник

• ← Что значит перпендикуляр в геометрии
• Что значит перпендикулярно в геометрии в трапеции →

Главная > Учебные материалы > Математика: Планиметрия. Страница 4
Рис.2 Теорема. Свойство диагоналей параллелограмма. 3.Ромб Теорема. диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.	Рис.3 Теорема. Свойство диагоналей ромба. Задача В параллелограмме АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. Необходимо найти отрезки ВЕ и ЕС, если АВ = 9 см, АD = 14 см (рис.4)	4.Теорема Фалеса Теорема: параллельные прямые, пересекающие стороны угла и отсекающие на одной его стороне равные отрезки, отсекают равные отрезки и на другой его стороне.	Рис.5 Теорема Фалеса. 5.Средняя линия треугольника Теорема. средняя линия треугольника, которая соединяет середины двух данных сторон, параллельна третьей его стороне и равна ее половине.	Рис.5 Теорема. Средняя линия треугольника. 6.Трапеция Теорема. средняя линия трапеции параллельна двум своим основаниям и равна их полусумме.	Рис.6 Теорема. Средняя линия трапеции. 7.Теорема о пропорциональных отрезках Теорема. параллельные прямые, которые пересекают стороны угла, отсекают от его сторон пропорциональные отрезки. Доказательство. Пусть дан угол и пересекающие его параллельные прямые. Необходимо доказать, что AС 1 /AС = AВ 1 /AВ (Рис. 7).	Рис.7 Теорема о пропорциональных отрезках. Т.е. мы пришли к противоречию, так как изначально мы взяли отрезок АС 2 = АС*АВ 1 /АВ.	Рис.8 Теорема о пропорциональных отрезках.