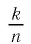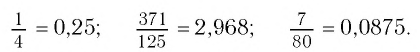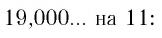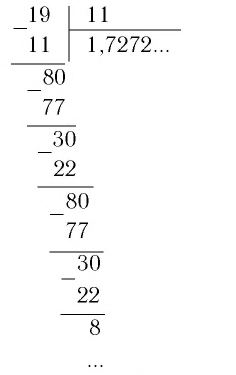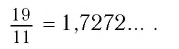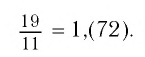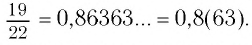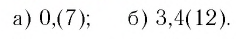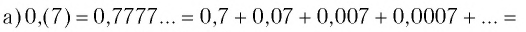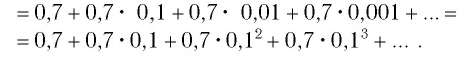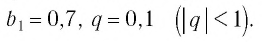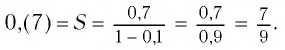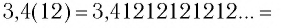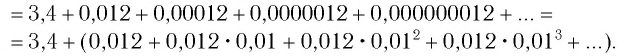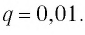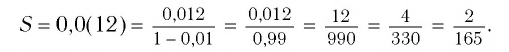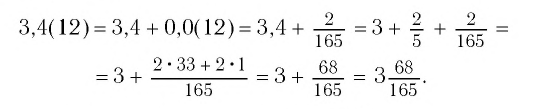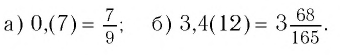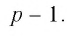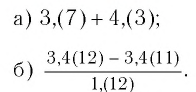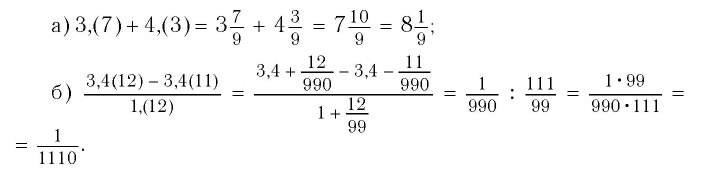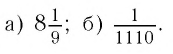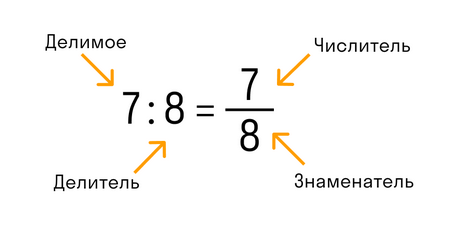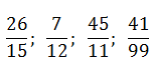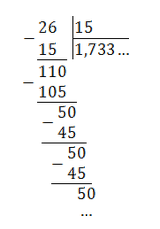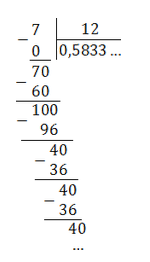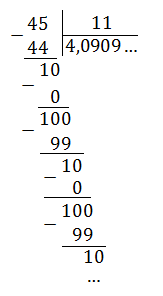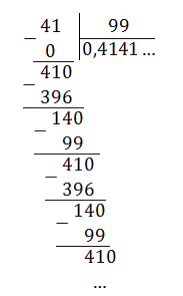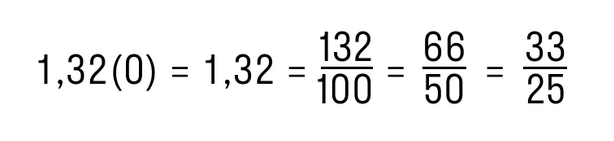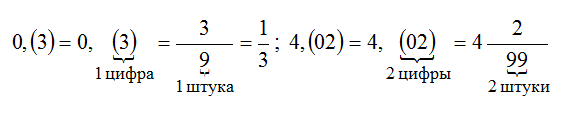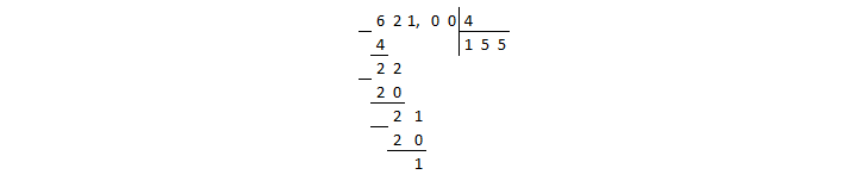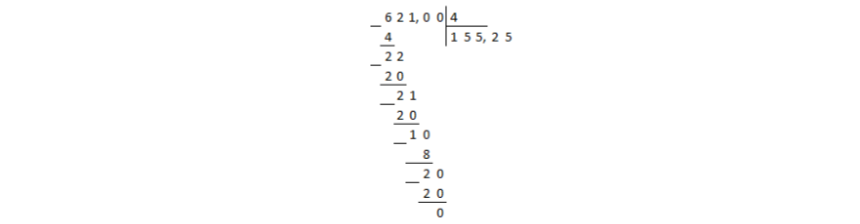Что значит периодическая дробь

Периодическая дробь

Имеет особую форму записи: целая часть в десятичной системе счисления, затем запятая и затем дробная часть в десятичной системе счисления, причём количество цифр дробной части строго определяется размерностью дробной части: если это десятые доли, дробная часть записывается одной цифрой; если тысячные — тремя; десятитысячные — четырьмя и т. д.

Примеры

обыкновенная дробь	десятичная дробь
4 /10	0,4
79 395 /1000	79,395

Очевидно, в начало целой части и/или в конец дробной части можно дописывать сколько угодно нулей.

Существуют также бесконечные десятичные дроби — периодические и непериодические. Например, ⅓ записывается как бесконечная периодическая дробь 0,3333… или 0,(3). А число π записывается как бесконечная непериодическая дробь 3,141592…

Периодическая десятичная дробь называется чистой периодической дробью, если её период (группа повторяющихся цифр) начинается сразу после запятой, а период может содержать любое конечное число цифр. Так, дробь 1,(3) — чистая периодическая дробь. Если периодическая десятичная дробь содержит ещё число, заключённое между целой частью и периодом, то такая периодическая дробь называется смешанной; число периодической дроби, стоящее между целой частью и периодом, называется предпериодом этой дроби.

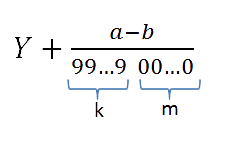
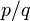
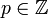
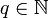
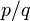
Очевидно, что всякая периодическая дробь является рациональным числом вида , где , . Верно и обратное утверждение: всякое рациональное число вида можно представить в виде десятичной периодической дроби.

Произношение десятичных дробей

В русском языке десятичные дроби читаются так: сначала произносится целая часть, потом слово «целых» («целая»), потом десятичная часть так, как если бы всё число состояло только из этой части, то есть числитель дроби — количественное числительное женского рода (одна, две, восемь и т. д.), а знаменатель — порядковое числительное (седьмая, сотая, двести тридцатая и т. д.).

Однако на практике часто встречается такое произношение: целая часть, союз «и», дробная часть.

Источник

Периодические дроби с примерами решения

Каждое рациональное число является действительным числом, а поэтому может быть записано в виде десятичной дроби — конечной или бесконечной. Хорошо известно, как это делается, когда

Применим теперь этот метод обращения обыкновенной дроби в десятичную к числу 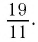Для этого разделим

Таким образом,

Бесконечная дробь, стоящая в правой части этого равенства, содержит периодически повторяющуюся группу цифр 72. Эта группа цифр называется периодом дроби, а сама дробь — периодической. При записи таких дробей период заключают в скобки и пишут один раз:

(Читается: «Одна целая семьдесят два в периоде».)

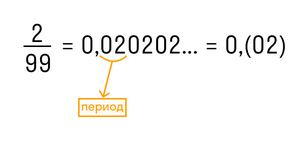
Еще один пример:

(Читается: «Нуль целых восемь десятых шестьдесят три в периоде».)

Приписывая к конечной десятичной дроби бесконечно много нулей, мы получаем бесконечную десятичную дробь. Поэтому конечные десятичные дроби тоже считаются периодическими с периодом 0. (При делении двух натуральных чисел не могут получиться дроби с числом 9 в периоде, поэтому в школьном курсе алгебры их не рассматривают.)

Приведенные примеры дают возможность догадаться, что каждое рациональное число записывается в виде бесконечной десятичной периодической дроби.

Чтобы в этом убедиться, заметим, что для обращения обыкновенной дроби 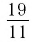в десятичную мы на каждом шаге остаток от деления (он был равен либо 8, либо 3) умножали на 10 и делили на 11. Но при делении на 11 вообще возможны лишь 11 различных остатков. Значит, на каком-то шаге остаток обязательно повторится (в нашем примере это случилось на третьем шаге), и поэтому в результате деления должна получиться периодическая дробь.

Наоборот, каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число.

Каждую периодическую десятичную дробь можно рассматривать либо как сумму бесконечно убывающей геометрической прогрессии, либо как сумму конечной десятичной дроби и сумму бесконечно убывающей геометрической прогрессии. Это позволяет представлять периодические десятичные дроби в виде обыкновенных дробей.

Пример №1

Обратить в обыкновенную дробь число:

Решение:

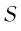
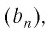
Таким образом, число 0,(7) есть — сумма бесконечно убывающей геометрической прогрессии где

Значит,

б)

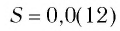
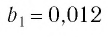
Сумму, стоящую в скобках, обозначим буквой S. Тогда есть сумма бесконечно убывающей геометрической прогрессии с первым членом и знаменателем

Значит,

Ответ:

Изучением периодических дробей занимался великий немецкий математик К- Ф. Гаусс (1777—1855). Уже в детстве он делил единицу на все подряд простые числа р из первой тысячи. При этом Гаусс подметил, что, начиная с какого-то места, десятичные знаки начинают повторяться, т. е. получаются периодические десятичные дроби. А периоды некоторых дробей достигали нескольких сотен десятичных знаков. Рассматривая эти примеры, Гаусс установил, что число цифр в периоде всегда является делителем числа

Пример №2

Найти значение выражения:

Решение:

Обратив каждое из чисел в обыкновенную дробь (см. пример 1), получим:

Ответ:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Как перевести периодическую дробь

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

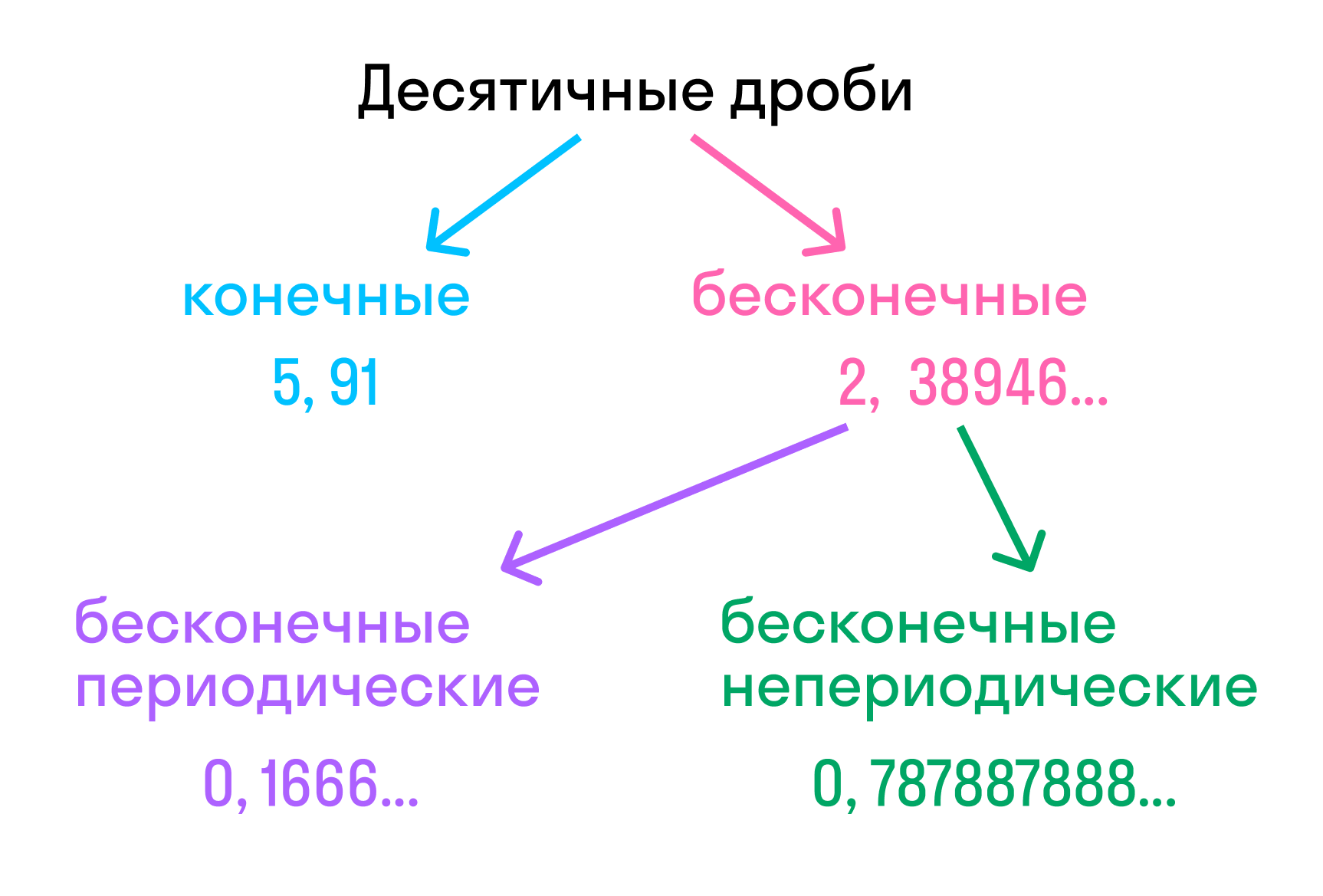
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Переход к периодической десятичной дроби

Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Тут есть два варианта:

Чтобы задать периодическую десятичную дробь, нужно найти ее периодическую и непериодическую часть. Чтобы это сделать нужно привести дробь в неправильную, а затем разделить числитель на знаменатель столбиком.

Что будет происходить в процессе:

Повторяющиеся цифры после десятичной точки нужно обозначить периодической частью, а то, что стоит спереди — непериодической.

Пример. Перевести обыкновенные дроби в периодические десятичные:

Все дроби без целой части, поэтому просто делим числитель на знаменатель уголком:

Определение периодической дроби

Периодическая дробь — это бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определенная группа цифр.

Периодическая часть дроби — это набор повторяющихся цифр, из которых состоит значащая часть.

В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».

Остальной отрезок значащей части, который не повторяется, называется непериодической частью.

Виды периодических дробей: чистые и смешанные.

Чистая периодическая десятичная дробь — это десятичная дробь, в записи которой сразу после запятой следует период. Например: 1,(4); 4,(25); 21,(693).

Смешанная периодическая десятичная дробь — это десятичная дробь, в записи которой после запятой через одну или несколько цифр начинается период. Например: 3,5(1); 0,02(89); 7,0(123) и т.д.

Рассмотрим примеры дробей, чтобы научиться определять части и период.

Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.

Читаем так: ноль целых три в периоде.

7/12 = 0,583333. = 0,58(3)

Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.

Читаем так: ноль целых пятьдесят восемь сотых и три в периоде.

17/11 = 1,545454. = 1,(54)

Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.

Читаем так: одна целая пятьдесят четыре сотых в периоде.

25/39 = 0,641025 641025. = 0,(641025)

Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6.

Читаем так: ноль целых шестьсот сорок одна двадцать пять миллионных в периоде.

пятьдесят четыре сотых в периоде.

9200/3 = 3066,666. = 3066,(6)

Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.

Читаем так: три тысячи шестьдесят шесть целых и шесть в периоде.

Перевод периодической дроби в обыкновенную

Давайте разберемся, как перевести периодическую десятичную дробь в обыкновенную дробь.

Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.

Пример. Преобразуем периодическую дробь 1,32(0) в обыкновенную.

Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:

Рассмотрим пример, в котором период дроби отличен от нуля.

Как записать периодическую дробь 10,0219(37) в виде обыкновенной:

В нашем примере k = 2.

Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначим полученное число — a.

Теперь осталось подставить все найденные значения в формулу и получить ответ:

Вот так мы справились с задачей представить бесконечную периодическую дробь в виде обыкновенной.

Есть еще один способ преобразовать периодическую дробь в обыкновенную. Для этого нужно рассматреть периодическую часть как сумму членов геометрический прогрессии, которая убывает. Например, вот так:

Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0

Перевод чистой периодической дроби в обыкновенную

Напомним: отличие чистой периодической десятичной дроби в том, что в ней сразу после запятой следует период.

Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период, а в знаменателе записать столько девяток, сколько цифр в периоде. Вот так:

Перевод смешанной периодической дроби в обыкновенную

Отличие смешанной периодической десятичной дроби в том, что после запятой через одну или несколько цифр начинается период.

Чтобы записать смешанную периодическую дробь в виде обыкновенной, нужно из числа, которое стоит до второго периода вычесть число, стоящее до первого периода, и записать результат в числителе.

А в знаменатель нужно поставить число, которое содержит столько девяток, сколько цифр в периоде, нулей в конце и сколько цифр между запятой и периодом.

Например, запишем 2,34(2) в виде обыкновенной дроби:

Источник

Периодические десятичные дроби

Вы будете перенаправлены на Автор24

Бесконечные десятичные дроби

Десятичные дроби после запятой могут содержать бесконечное количество цифр.

Бесконечную десятичную дробь практически невозможно записать полностью, поэтому при их записи ограничиваются только некоторым конечным количеством цифр после запятой, после чего ставят многоточие, которое указывает на бесконечно продолжающуюся последовательность цифр.

Периодические десятичные дроби

Готовые работы на аналогичную тему

Бесконечные десятичные периодические дроби представляются рациональными числами. Другими словами, любая периодическая дробь может быть переведена в обыкновенную дробь, а любая обыкновенная дробь может быть представлена в виде периодической дроби.

Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби

Для остальных случаев используется другой способ перевода обыкновенной дроби в десятичную>:

числитель нужно заменить десятичной дробью с любым числом нулей после десятичной запятой;

разделить числитель дроби на знаменатель (деление выполняется как деление натуральных чисел в столбик, а в частном ставят десятичную запятую после окончания деления целой части делимого).

Решение.

Деление дошло до десятичной запятой в делимом, а остаток при этом получили не нулевой. В таком случае в частном ставится десятичная запятая и продолжается деление столбиком, не взирая на запятые:

В остатке получили нуль, значит деление окончено.

Для перевода обыкновенной дроби в десятичную выполним деление в столбик:

Общий вывод о переводе обыкновенных дробей в десятичные:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 10 06 2021

Источник

Перевод периодической дроби в обыкновенную дробь

Содержание

Периодические дроби – очень интересное явление. Только представьте себе дробь, у которой нет конца, и её «хвост» длится и длится.

Иногда возникает необходимость записать периодическую дробь в виде обыкновенной. Получается, что вместо числа мы пишем пример – ведь знак дроби обозначает знак деления.

Давайте разберёмся, как это сделать.

Состав периодической дроби

Прежде чем мы начнём превращать периодические дроби в обыкновенные, нам необходимо разобраться, как называются части периодических дробей. Это нам понадобится.

Итак, на первом месте – целая часть периодической дроби.

Всё, что после запятой, будет дробной частью.

У чистых периодических дробей дробная часть состоит из периода (повтораяющейся части дроби). Она взята в скобки. В скобках может быть не одна, а несколько цифр. Количество цифр в скобках называется длиной периода.

В смешанной периодической дроби между запятой и периодом есть ещё одна или несколько цифр. Эти цифры в период не входят, то есть не повторяются. Надо сказать, что в разных пособиях эта часть дроби может называться по-разному. Иногда ей не дают никакого названия, и просто пишут «цифры между запятой и периодом». Но также эту часть называют непериодической частью или предпериодом.

Перевод чистых периодических дробей в обыкновенные дроби

С чистыми периодическими дробями (то есть с теми, у которых период начинается сразу после запятой) всё очень просто. Для них существует простой алгоритм.

После того, как дробь записана, её можно сократить, разделив числитель и знаменатель на одинаковое число.

Перевод смешанных периодических дробей в обыкновенные дроби

Со смешанными дробями дело обстоит сложнее, тут нужно запомнить более длинный алгоритм действий. Кроме того, нужно хорошо знать названия всех частей периодической дроби, чтобы не запутаться.

Для перевода смешанной периодической дроби в обыкновенную нужно:
1) записать целую часть дроби (если она есть) без изменений
2) записать в виде числителя разность дробной части периодической дроби (записываем её без скобок, как если бы это было натуральное число) и предпериода (непериодической части) дроби
3) записать в виде знаменателя число, состоящее из девяток и нулей, где число девяток равно длине периода, а нулей – длине предпериода.

Выглядит очень длинно и сложно! Но проделав подобные вычисления несколько раз, вы сможете выполнять их без особого труда.

Целую часть записываем без изменений, переходим к дробной.

Разберём ещё один пример.

В знаменателе пишем одну девятку, так как длина периода равна одному, и два ноля, так как в непериодической части дроби у нас две цифры.

Уже после того, как вы переведёте несколько периодических дробей в обыкновенные, вы почувствуете, что алгоритм запомнился и уже не кажется таким сложным. Также хорошо проверять свои вычисления при помощи калькулятора, разделяя числитель полученной дроби на знаменатель.

Источник