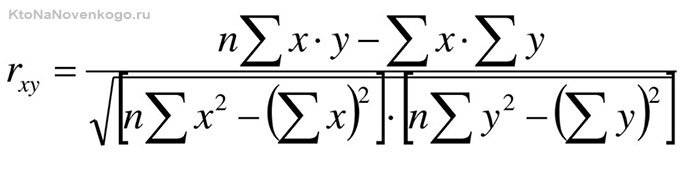Что значит переменные коррелируют

Что такое корреляция и что означает коррелировать — простыми словами о сложном

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Когда некоторые люди слышат слово «корреляция», то зачастую просто впадают в ступор. Оно и понятно: жуткий термин из мира высшей математики и статистики.

Сразу представляются унылые графики, многоэтажные формулы, при взгляде на которые хочется забиться в угол и плакать. На самом деле все гораздо проще.

Потратив несколько минут на прочтение этой статьи, вы узнаете, что такое корреляция и как ее использовать в повседневной жизни.

Определение корелляции — что это

Простыми словами корреляция – это взаимосвязь двух или нескольких случайных параметров. Когда одна величина растет или уменьшается, другая тоже изменяется.

Объясним на примере: существует корреляция между температурой воздуха и потреблением мороженого. Чем жарче погода, тем больше холодного лакомства покупают люди. И наоборот.

Такие закономерности устанавливаются путем исследования больших объемов статистических данных. Собираем информацию о потреблении мороженого за несколько лет и сведения о колебаниях температуры за тот же период. А дальше сопоставляем и ищем зависимость.

Коррелировать – это значит быть взаимосвязанным с чем-то. Существует положительная и отрицательная корреляции.

При положительной чем больше один параметр, тем больше и другой. Например, чем масштабнее траты фермера на удобрения, тем обильнее урожай. При обратной корреляции рост одной величины сопровождается уменьшением другой. Чем выше здание, тем хуже оно противостоит землетрясениям.

Корреляция — это взаимосвязь без гарантий

Рассмотрим пример прямой корреляции: чем выше уровень благосостояния человека, тем больше его продолжительность жизни. Обеспеченные люди питаются качественной пищей и своевременно получают врачебную помощь. В отличие от бедняков.

Однако нельзя с уверенностью сказать, что определенный олигарх проживет дольше вот этого нищего.

Это лишь статистическая вероятность, которая может не сработать для одного конкретного случая. Этим корреляция отличается от линейной зависимости, где исход известен со 100-процентной вероятностью.

Но если мы возьмем выборку из сотни тысяч богачей и такого же числа малоимущих, сравним их продолжительность жизни, то общая тенденция будет верна.

Коэффициент корреляции

Величина коэффициента корреляции рассчитывается по формуле:

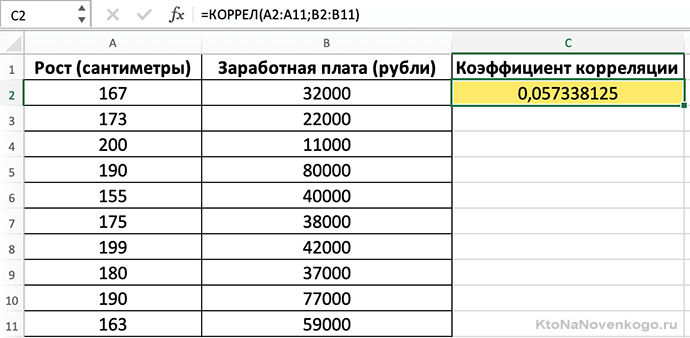
Если внезапно потемнело в глазах и возникло непреодолимое желание закрыть статью (синдром гуманитария), то есть вариант попроще. Microsoft Exel все выполнит сам при помощи функции «КОРРЕЛ». Делается это так:

Судя по расчетам, рост человека практически никак не влияет на уровень зарплаты.

Реальные причины корреляции и возможные гипотезы

Курс доллара и стоимость нефти отрицательно коррелируют. Можем выдвинуть гипотезу: повышение цен на черное золото вызывает падение стоимости американской валюты. Но почему так происходит? Откуда взялась связь между этими явлениями?

Определение причины корреляции – это очень сложная задача. Переплетаются тысячи различных факторов, часть из которых скрыта.

Возможно, дело в том, что США – крупнейший потребитель нефти в мире. Каждый день они импортируют около 7,2 миллиона баррелей. Снижение цены на черное золото – хорошо для американской экономики, ведь позволяет тратить меньше денег. Следовательно, доллар растет.

Корреляция предоставляет возможность сделать вывод из статистических данных.

Например, мы выяснили, что существует отрицательная взаимосвязь между доходом персонала и его эффективностью в работе. Наша гипотеза: «Лентяи и бездельники получают больше, чем ответственные сотрудники». Тогда мы пересмотрим систему мотивации и избавимся от бесполезных людей.

Гипотеза – это лишь статистический вывод, предположение. Она вполне может оказаться ошибочной.

Согласно статистике, чем больше пожарных участвует в тушении огня, тем существенней размер ущерба. Какую гипотезу можем сделать отсюда? Пожарные приносят вред, давайте сократим их! Но если разобраться, то настоящая причина повреждения – это огонь. А увеличение числа лиц, задействованных в его тушении, – следствие масштаба пожара.

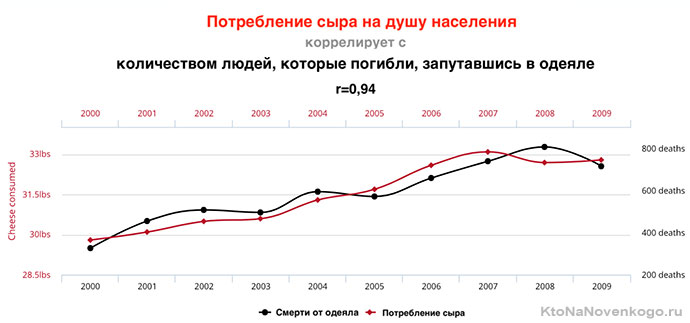
Наша вселенная бесконечна, а значит всегда можно найти несколько переменных, которые будут коррелировать между собой, несмотря на полное отсутствие причинно-следственных связей. Даже самое буйное воображение не сможет объяснить, что объединяет сыр и одеяло-убийцу:

Более подробно на эту тему смотрите в видео:

Как при помощи корреляции люди становятся богаче

Главное правило любого инвестора: не класть все яйца в одну корзину. Вложения рекомендуется диверсифицировать (что это?) – распределять. Поэтому люди покупают акции не одной компании, а десятка разных, формируя инвестиционные портфели. Если котировки какой-то фирмы упадут, то оставшиеся девять смогут отыграть падение или хотя бы уменьшить убытки.

Но это в теории, а на практике все портит корреляция. Проблема в том, что стоимости акций разных компаний внутри отрасли или даже всей страны могут сильно коррелировать. Проблемы огромной корпорации провоцируют панику на рынке, снижают стоимость иных активов, на первый взгляд не связанных между собой. В 2008 году случился крах Lehman Brothers, который вызвал цепную реакцию и обвал на мировых рынках.

Поэтому при инвестировании нужно стараться выбирать направления, которые не связаны между собой (r стремится к 0).

Территориальное приближение активов друг к другу усиливает корреляцию. Значит, нужно рассматривать варианты в разных точках мира, максимально удаленных друг от друга.

В жизни этот принцип тоже действует. Если ваши навыки и знания позволяют трудиться программистом, таксистом, сантехником и журналистом – вы хорошо защищены от риска безработицы.

Памятка

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (12)

Отличная статья! Спасибо! Все доступно к пониманию.

Скажите, пожалуйста, если некий факт N напрямую обусловлен фактом М, то есть без M не было бы N вообще, то корректно ли говорить о том, что N коррелирует с M?

Спасибо за статью. Кратко, четко, ясно.

«Корреляция — это взаимозависимость СЛУЧАЙНЫХ факторов. Она отображает ПРИБЛИЖЕННУЮ взаимосвязь и не дает точных ответов»

Выше цитата для Анны, т.е. «если некий факт N напрямую обусловлен фактом М,» то ИМХО это противоречит «взаимозависимости СЛУЧАЙНЫХ факторов» и «ПРИБЛИЖЕННОЙ взаимосвязи»

Все люди должны иметь хотя бы поверхностные знания об экономике, хотя многие ошибочно полагают, что их это не касается. В том числе важно понимать взаимосвязи между факторами, чтоб эффективно вести даже маленькое домохозяйство.

Не обязательно понимать сложные формулы корреляции, чтоб знать что безработица и стагнация сказываются на жизни всех граждан страны.

Это слово я слышала всего несколько раз за всю жизнь и каждый раз приходится гуглить. Ну почему нельзя давать определение проще? Напридумывают же сложных слов, а ты голову ломай.

Статья — супер! Спасибо большое.

Благодарю за статью. Доступно и понятно. Даже для тех у кого « синдром гуманитария»

Источник

Корреляции для начинающих

Апдейт для тех, кто сочтет статью полезной и занесет в избранное. Есть приличный шанс, что пост уйдет в минуса, и я буду вынужден унести его в черновики. Сохраняйте копию!

Краткий и несложный материал для неспециалистов, рассказывающий в наглядной форме о различных методах поиска регрессионных зависимостей. Это все и близко не академично, зато надеюсь что понятно. Прокатит как мини-методичка по обработке данных для студентов естественнонаучных специальностей, которые математику знают плохо, впрочем как и автор. Расчеты в Матлабе, подготовка данных в Экселе — так уж повелось в нашей местности

Введение

Зачем это вообще надо? В науке и около нее очень часто возникает задача предсказания какого-то неизвестного параметра объекта исходя из известных параметров этого объекта (предикторов) и большого набора похожих объектов, так называемой учебной выборки. Пример. Вот мы выбираем на базаре яблоко. Его можно описать такими предикторами: красность, вес, количество червяков. Но как потребителей нас интересует вкус, измеренный в попугаях по пятибалльной шкале. Из жизненного опыта нам известно, что вкус с приличной точностью равен 5*красность+2*вес-7*количество червяков. Вот про поиск такого рода зависимостей мы и побеседуем. Чтобы обучение пошло легче, попробуем предсказать вес девушки исходя из ее 90/60/90 и роста.

Исходные данные

В качестве объекта исследования возьму данные о параметрах фигуры девушек месяца Плейбоя. Источник — www.wired.com/special_multimedia/2009/st_infoporn_1702, слегка облагородил и перевел из дюймов в сантиметры. Вспоминается анекдот про то, что 34 дюйма — это как два семнадцатидюймовых монитора. Также отделил записи с неполной информацией. При работе с реальными объектами их можно использовать, но сейчас они нам только мешают. Зато их можно использовать для проверки адекватности полученных результатов. Все данные у нас непрерывные, то есть грубо говоря типа float. Они приведены к целым числам только чтобы не загромождать экран. Есть способы работы и с дискретными данными — в нашем примере это например может быть цвет кожи или национальность, которые принимают одно из фиксированного набора значений. Это больше имеет отношение к методам классификации и принятия решений, что тянет еще на один мануал. Data.xls В файле два листа. На первом собственно данные, на втором — отсеянные неполные данные и набор для проверки нашей модели.

Обозначения

W — вес реальный
W_p — вес, предсказанный нашей моделью
S — бюст
T — талия
B — бедра
L — рост
E — ошибка модели

Как оценить качество модели?

Задача нашего упражнения — получить некую модель, которая описывает какой-либо объект. Способ получения и принцип работы конкретной модели нас пока не волнует. Это просто функция f(S, T, B, L), которая выдает вес девушки. Как понять, какая функция хорошая и качественная, а какая не очень? Для этого используется так называемая fitness function. Самая классическая и часто используемая — это сумма квадратов разницы предсказанного и реального значения. В нашем случае это будет сумма (W_p — W)^2 для всех точек. Собственно, отсюда и пошло название «метод наименьших квадратов». Критерий не лучший и не единственный, но вполне приемлемый как метод по умолчанию. Его особенность в том, что он чувствителен по отношению к выбросам и тем самым, считает такие модели менее качественными. Есть еще всякие методы наименьших модулей итд, но сейчас нам это пока не надо.

Простая линейная регрессия

Самый простой случай. У нас одна переменная-предиктор и одна зависимая переменная. В нашем случае это может быть например рост и вес. Нам надо построить уравнение W_p = a*L+b, т.е. найти коэффициенты a и b. Если мы проведем этот расчет для каждого образца, то W_p будет максимально совпадать с W для того же образца. То есть у нас для каждой девушки будет такое уравнение:
W_p_i = a*L_i+b
E_i = (W_p-W)^2

Общая ошибка в таком случае составит sum(E_i). В результате, для оптимальных значений a и b sum(E_i) будет минимальным. Как же найти уравнение?

Матлаб

Графичек

Мда, негусто. Это график W_p(W). Формула на графике показывает связь W_p и W. В идеале там будет W_p = W*1 + 0. Вылезла дискретизация исходных данных — облако точек клетчатое. Коэффициент корреляции ни в дугу — данные слабо коррелированы между собой, т.е. наша модель плохо описывает связь веса и роста. По графику это видно как точки, расположенные в форме слабо вытянутого вдоль прямой облака. Хорошая модель даст облако растянутое в узкую полосу, еще более плохая — просто хаотичный набор точек или круглое облако. Модель необходимо дополнить. Про коэффициент корреляции стоит рассказать отдельно, потому что его часто используют абсолютно неправильно.

Расчет в матричном виде

Мультилинейная регрессия

Попытка номер два

А так получше, но все равно не очень. Как видим, клетчатость осталась только по горизонтали. Никуда не денешься, исходные веса были целыми числами в фунтах. То есть после конверсии в килограммы они ложатся на сетку с шагом около 0.5. Итого финальный вид нашей модели:

W_p = 0.2271*S + 0.1851*T + 0.3125*B + 0.3949*L — 72.9132

Объемы в сантиметрах, вес в кг. Поскольку у нас все величины кроме роста в одних единицах измерения и примерно одного порядка по величине (кроме талии), то мы можем оценить их вклады в общий вес. Рассуждения примерно в таком духе: коэффициент при талии самый маленький, равно как и сами величины в сантиметрах. Значит, вклад этого параметра в вес минимален. У бюста и особенно у бедер он больше, т.е. сантиметр на талии дает меньшую прибавку к массе, чем на груди. А больше всего на вес влияет объем задницы. Впрочем, это знает любой интересующийся вопросом мужчина. То есть как минимум, наша модель реальной жизни не противоречит.

Валидация модели

Название громкое, но попробуем получить хотя бы ориентировочные веса тех девушек, для которых есть полный набор размеров, но нет веса. Их 7: с мая по июнь 1956 года, июль 1957, март 1987, август 1988. Находим предсказанные по модели веса: W_p=X*repr

Что ж, по крайней мере в текстовом виде выглядит правдоподобно. А насколько это соответствует реальности — решать вам

Применимость

Если вкратце — полученная модель годится для объектов, подобных нашему набору данных. То есть по полученным корреляциям не стоит считать параметры фигур женщин с весом 80+, возрастом, сильно отличающимся от среднего по больнице итд. В реальных применениях можно считать, что модель пригодна, если параметры изучаемого объекта не слишком отличаются от средних значений этих же параметров для исходного набора данных. Могут возникнуть (и возникнут) проблемы, если у нас предикторы сильно коррелированы между собой. То есть, например это рост и длина ног. Тогда коэффициенты для соответствующих величин в уравнении регрессии будут определены с малой точностью. В таком случае надо выбросить один из параметров, или воспользоваться методом главных компонент для снижения количества предикторов. Если у нас малая выборка и/или много предикторов, то мы рискуем попасть в переопределенность модели. То есть если мы возьмем 604 параметра для нашей выборки (а в таблице всего 604 девушки), то сможем аналитически получить уравнение с 604+1 слагаемым, которое абсолютно точно опишет то, что мы в него забросили. Но предсказательная сила у него будет весьма невелика. Наконец, далеко не все объекты можно описать мультилинейной зависимостью. Бывают и логарифмические, и степенные, и всякие сложные. Их поиск — это уже совсем другой вопрос.

Источник

ПЕРЕМЕННЫЕ КОРРЕЛИРУЮЩИЕ

Смотреть что такое «ПЕРЕМЕННЫЕ КОРРЕЛИРУЮЩИЕ» в других словарях:

ПЕРЕМЕННЫЕ КОРРЕЛИРУЮЩИЕ — См. КОРРЕЛЯЦИЯ … Толковый словарь по социологии

Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора

Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора

Факторный анализ — Факторный анализ многомерный метод, применяемый для изучения взаимосвязей между значениями переменных. Предполагается, что известные переменные зависят от меньшего количества неизвестных переменных и случайной ошибки. Содержание 1 Краткая… … Википедия

Эконометрика как наука — Эконометрика наука, изучающая конкретные количественные и качественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей. Определение предмета эконометрики было дано в уставе… … Википедия

Экономическая статистика — Эконометрика наука, изучающая конкретные количественные и качественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей. Определение предмета эконометрики было дано в уставе… … Википедия

Время реакции (reaction time) — Измерение времени реакции (ВР), вероятно, самый почтенный предмет в эмпирической психологии. Оно зародилось в области астрономии, в 1823 г., с измерением индивидуальных различий в скорости восприятия пересечения звездой линии риски телескопа. Эти … Психологическая энциклопедия

Социолингвистическое измерение — Способ упорядочения, классификации информации в статистике, упорядочение данных, информирующих о взаимосвязанных лингвистических и экстралингвистических факторах. С.и. направлено на определение лингвистически и коммуникативно значимых… … Словарь социолингвистических терминов

социолингвистическое измерение — Способ упорядочения, классификации информации о взаимосвязанных лингвистических и экстралингвистических факторах, направленный на определение лингвистически и коммуникативно значимых переменных в речи представителей различных групп: 1)… … Словарь лингвистических терминов Т.В. Жеребило

Источник

Python, корреляция и регрессия: часть 1

Чем больше я узнаю людей, тем больше мне нравится моя собака.

В этой серии постов будет рассмотрена линейная регрессия. При наличии выборки данных наша модель усвоит линейное уравнение, позволяющее ей делать предсказания о новых, не встречавшихся ранее данных. Для этого мы снова обратимся к библиотеке pandas и изучим связь между ростом и весом спортсменов-олимпийцев. Мы введем понятие матриц и покажем способы управления ими с использованием библиотеки pandas.

О данных

В этой серии постов используются данные, любезно предоставленные компанией Guardian News and Media Ltd., о спортсменах, принимавших участие в Олимпийских Играх 2012 г. в Лондоне. Эти данные изначально были взяты из блога газеты Гардиан.

Обследование данных

Когда вы сталкиваетесь с новым набором данных, первая задача состоит в том, чтобы его обследовать с целью понять, что именно он содержит.

Файл all-london-2012-athletes.tsv достаточно небольшой. Мы можем обследовать данные при помощи pandas, как мы делали в первой серии постов «Python, исследование данных и выборы», воспользовавшись функцией read_csv :

Если выполнить этот пример в консоли интерпретатора Python либо в блокноте Jupyter, то вы должны увидеть следующий ниже результат:

Столбцы данных (нам повезло, что они ясно озаглавлены) содержат следующую информацию:

страна, за которую он выступает

дата рождения в виде строки

место рождения в виде строки (со страной)

число выигранных золотых медалей

число выигранных серебряных медалей

число выигранных бронзовых медалей

всего выигранных золотых, серебряных и бронзовых медалей

вид спорта, в котором он соревновался

состязание в виде списка, разделенного запятыми

Даже с учетом того, что данные четко озаглавлены, очевидно присутствие пустых мест в столбцах с ростом, весом и местом рождения. При наличии таких данных следует проявлять осторожность, чтобы они не сбили с толку.

Визуализация данных

В первую очередь мы рассмотрим разброс роста спортсменов на Олимпийских играх 2012 г. в Лондоне. Изобразим эти значения роста в виде гистограммы, чтобы увидеть характер распределения данных, не забыв сначала отфильтровать пропущенные значения:

Этот пример сгенерирует следующую ниже гистограмму:

Как мы и ожидали, данные приближенно нормально распределены. Средний рост спортсменов составляет примерно 177 см. Теперь посмотрим на распределение веса олимпийских спортсменов:

Приведенный выше пример сгенерирует следующую ниже гистограмму:

К счастью, эта асимметрия может быть эффективным образом смягчена путем взятия логарифма веса при помощи функции библиотеки numpy np.log :

Этот пример сгенерирует следующую ниже гистограмму:

Теперь данные намного ближе к нормальному распределению. Из этого следует, что вес распределяется согласно логнормальному распределению.

Логнормальное распределение

Логнормальное распределение — это распределение набора значений, чей логарифм нормально распределен. Основание логарифма может быть любым положительным числом за исключением единицы. Как и нормальное распределение, логнормальное распределение играет важную роль для описания многих естественных явлений.

Логарифм показывает степень, в которую должно быть возведено фиксированное число (основание) для получения данного числа. Изобразив логарифмы на графике в виде гистограммы, мы показали, что эти степени приближенно нормально распределены. Логарифмы обычно берутся по основанию 10 или основанию e, трансцендентному числу, приближенно равному 2.718. В функции библиотеки numpy np.log и ее инверсии np.exp используется основание e. Выражение log_e также называется натуральным логарифмом, или ln, из-за свойств, делающих его особенно удобным в исчислении.

Логнормальное распределение обычно имеет место в процессах роста, где темп роста не зависит от размера. Этот феномен известен как закон Джибрэта, который был cформулирован в 1931 г. Робертом Джибрэтом, заметившим, что он применим к росту фирм. Поскольку темп роста пропорционален размеру, более крупные фирмы демонстрируют тенденцию расти быстрее, чем фирмы меньшего размера.

Нормальное распределение случается в ситуациях, где много мелких колебаний, или вариаций, носит суммирующий эффект, тогда как логнормальное распределение происходит там, где много мелких вариаций имеет мультипликативный эффект.

С тех пор выяснилось, что закон Джибрэта применим к большому числу ситуаций, включая размеры городов и, согласно обширному математическому ресурсу Wolfram MathWorld, к количеству слов в предложениях шотландского писателя Джорджа Бернарда Шоу.

В остальной части этой серии постов мы будем использовать натуральный логарифм веса спортсменов, чтобы наши данные были приближенно нормально распределены. Мы выберем популяцию спортсменов примерно с одинаковыми типами телосложения, к примеру, олимпийских пловцов.

Визуализация корреляции

Один из самых быстрых и самых простых способов определить наличие корреляции между двумя переменными состоит в том, чтобы рассмотреть их на графике рассеяния. Мы отфильтруем данные, выбрав только пловцов, и затем построим график роста относительно веса спортсменов:

Этот пример сгенерирует следующий ниже график:

Результат ясно показывает, что между этими двумя переменными имеется связь. График имеет характерно смещенную эллиптическую форму двух коррелируемых, нормально распределенных переменных с центром вокруг среднего значения. Следующая ниже диаграмма сравнивает график рассеяния с распределениями вероятностей роста и логарифма веса:

Точки, близко расположенные к хвосту одного распределения, также демонстрируют тенденцию близко располагаться к тому же хвосту другого распределения, и наоборот. Таким образом, между двумя распределениями существует связь, которую в ближайших нескольких разделах мы покажем, как определять количественно. Впрочем, если мы внимательно посмотрим на предыдущий график рассеяния, то увидим, что из-за округления измерений точки уложены в столбцы и строки (в см. и кг. соответственно для роста и веса). Там, где это происходит, иногда желательно внести в данные искажения, которые также называются сдвигом или джиттером с тем, чтобы яснее показать силу связи. Без генерирования джиттера (в виде случайных отклонений) может оказаться, что, то, что по внешнему виду составляет одну точку, фактически представляет много точек, которые обозначены одинаковой парой значений. Внесение нескольких случайных помех делает эту ситуацию вряд ли возможной.

Генерирование джиттера

График с джиттером выглядит следующим образом:

Как и в случае с внесением прозрачности в график рассеяния в первой серии постов об описательной статистике, генерирование джиттера — это механизм, который обеспечивает исключение несущественных факторов, таких как объем данных или артефакты округления, которые могут заслонить от нас возможность увидеть закономерности в данных.

Ковариация

Одним из способов количественного определения силы связи между двумя переменными является их ковариация. Она измеряет тенденцию двух переменных изменяться вместе.

Если у нас имеется два ряда чисел, X и Y, то их отклонения от среднего значения составляют:

Здесь x_i — это значение X с индексом i, y_i — значение Y с индексом i, x̅ — среднее значение X, и y̅ — среднее значение Y. Если X и Y проявляют тенденцию изменяться вместе, то их отклонения от среднего будет иметь одинаковый знак: отрицательный, если они — меньше среднего, положительный, если они больше среднего. Если мы их перемножим, то произведение будет положительным, когда у них одинаковый знак, и отрицательным, когда у них разные знаки. Сложение произведений дает меру тенденции этих двух переменных отклоняться от среднего значения в одинаковом направлении для каждой заданной выборки.

Ковариация определяется как среднее этих произведений:

На чистом Python ковариация вычисляется следующим образом:

В качестве альтернативы, мы можем воспользоваться функцией pandas cov :

Ковариация роста и логарифма веса для наших олимпийских пловцов равна 1.356, однако это число сложно интерпретировать. Единицы измерения здесь представлены произведением единиц на входе.

Стандартная оценка, англ. standard score, также z-оценка — это относительное число стандартных отклонений, на которые значение переменной отстоит от среднего значения. Положительная оценка показывает, что переменная находится выше среднего, отрицательная — ниже среднего. Это безразмерная величина, получаемая при вычитании популяционного среднего из индивидуальных значений и деления разности на популяционное стандартное отклонение.

Корреляция Пирсона

Корреляция Пирсона часто обозначается переменной r и вычисляется следующим образом, где отклонения от среднего dx_i и dy_i вычисляются как и прежде:

Поскольку для переменных X и Y стандартные отклонения являются константными, уравнение может быть упрощено до следующего, где σ_x и σ_y — это стандартные отклонения соответственно X и Y:

В таком виде формула иногда упоминается как коэффициент корреляции смешанных моментов Пирсона или попросту коэффициент корреляции и, как правило, обозначается буквой r.

Ранее мы уже написали функции для вычисления стандартного отклонения. В сочетании с нашей функцией с вычислением ковариации получится следующая ниже имплементация корреляции Пирсона:

В качестве альтернативы мы можем воспользоваться функцией pandas corr :

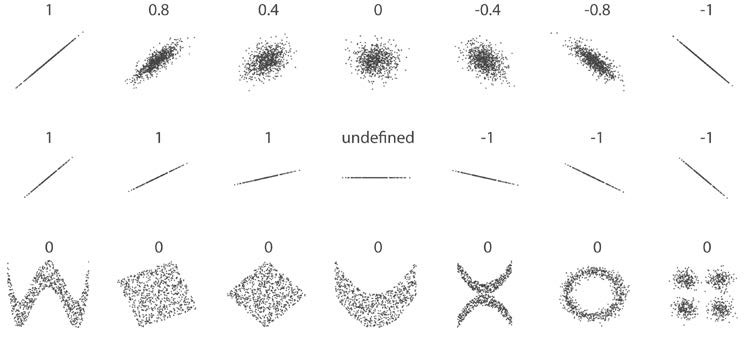
Правда, если r = 0, то с необходимостью вовсе не следует, что переменные не коррелируют. Корреляция Пирсона измеряет лишь линейные связи. Как продемонстрировано на следующих графиках, между переменными может существовать еще некая нелинейная связь, которую r не объясняет:

Отметим, что корреляция центрального примера не определена, потому что стандартное отклонение y = 0. Поскольку наше уравнение для r содержало бы деление ковариации на 0, то результат получается бессмысленным. В этом случае между переменными не может быть никакой корреляции; y всегда будет иметь среднее значение. Простое обследование стандартных отклонений это подтвердит.

Мы можем вычислить коэффициент корреляции для данных роста и логарифма веса наших пловцов следующим образом:

В результате получим ответ 0.867, который количественно выражает сильную, положительную корреляцию, уже наблюдавшуюся нами на точечном графике.

Выборочный r и популяционный ρ

Аналогично среднему значению и стандартному отклонению, коэффициент корреляции является сводной статистикой. Он описывает выборку; в данном случае, выборку спаренных значений: роста и веса. Коэффициент корреляции известной выборки обозначается буквой r, тогда как коэффициент корреляции неизвестной популяции обозначается греческой буквой ρ (рхо).

Как мы убедились в предыдущей серии постов о тестировании гипотез, мы не должны исходить из того, что результаты, полученные в ходе измерения нашей выборки, применимы к популяции в целом. К примеру, наша популяция может состоять из всех пловцов всех недавних Олимпийских игр. И будет совершенно недопустимо обобщать, например, на другие олимпийские виды спорта, такие как тяжелая атлетика или фитнес-плавание.

Даже в допустимой популяции — такой как пловцы, выступавшие на недавних Олимпийских играх, — наша выборка коэффициента корреляции является всего лишь одной из многих потенциально возможных. То, насколько мы можем доверять нашему r, как оценке параметра ρ, зависит от двух факторов:

Проверка статистических гипотез

В предыдущей серии постов мы познакомились с проверкой статистических гипотез, как средством количественной оценки вероятности, что конкретная гипотеза (как, например, что две выборки взяты из одной и той же популяции) истинная. Чтобы количественно оценить вероятность, что корреляция существует в более широкой популяции, мы воспользуемся той же самой процедурой.

В первую очередь, мы должны сформулировать две гипотезы, нулевую гипотезу и альтернативную:

Стандартная ошибка коэффициента корреляции r по выборке задается следующей формулой:

Эта формула точна, только когда r находится близко к нулю (напомним, что величина ρ влияет на нашу уверенность), но к счастью, это именно то, что мы допускаем согласно нашей нулевой гипотезы.

Мы можем снова воспользоваться t-распределением и вычислить t-статистику:

P-значение настолько мало, что в сущности равно 0, означая, что шанс, что нулевая гипотеза является истинной, фактически не существует. Мы вынуждены принять альтернативную гипотезу о существовании корреляции.

Интервалы уверенности

Установив, что в более широкой популяции, безусловно, существует корреляция, мы, возможно, захотим количественно выразить диапазон значений, внутри которого, как мы ожидаем, будет лежать параметр ρ, вычислив для этого интервал уверенности. Как и в случае со средним значением в предыдущей серии постов, интервал уверенности для r выражает вероятность (выраженную в %), что параметр ρ популяции находится между двумя конкретными значениями.

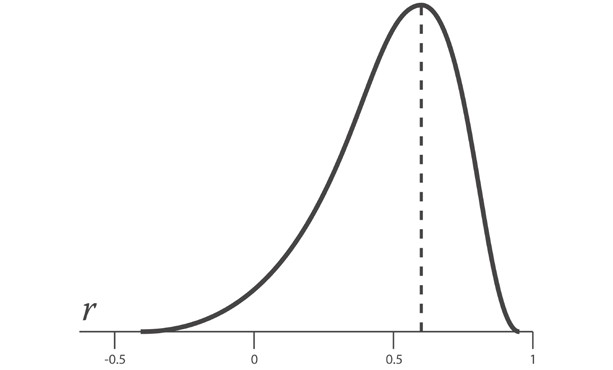
Однако при попытке вычислить стандартную ошибку коэффициента корреляции возникает сложность, которой не было в случае со средним значением. Поскольку абсолютное значение коэффициента корреляции r не может превышать 1, распределение возможных выборок коэффициентов корреляции r смещается по мере приближения r к пределу своего диапазона.

Приведенный выше график показывает отрицательно скошенное распределение r-выборок для параметра ρ, равного 0.6.

К счастью, трансформация под названием z-преобразование Фишера стабилизирует дисперсию r по своему диапазону. Она аналогична тому, как наши данные о весе спортсменов стали нормально распределенными, когда мы взяли их логарифм.

Уравнение для z-преобразования следующее:

Стандартная ошибка z равна:

Таким образом, процедура вычисления интервалов уверенности состоит в преобразовании r в z с использованием z-преобразования, вычислении интервала уверенности в терминах стандартной ошибки SE_z и затем преобразовании интервала уверенности в r.

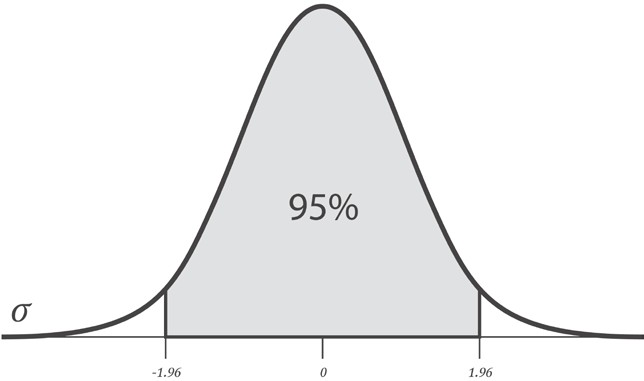
В целях вычисления интервала уверенности в терминах SE_z, мы можем взять число стандартных отклонений от среднего, которое дает нам требуемый уровень доверия. Обычно используют число 1.96, так как оно является числом стандартных отклонений от среднего, которое содержит 95% площади под кривой. Другими словами, 1.96 стандартных ошибок от среднего значения выборочного r содержит истинную популяционную корреляцию ρ с 95%-ой определенностью.

Однако, как показано на приведенном выше графике, мы хотели бы вычесть ту же самую величину, т.е. 2.5%, из каждого хвоста с тем, чтобы 95%-й интервал уверенности был центрирован на нуле. Для этого при выполнении двусторонней проверки нужно просто уменьшить разность наполовину и вычесть результат из 100%. Так что, требуемый уровень доверия в 95% означает, что мы обращаемся к критическому значению 97.5%:

Поэтому наш 95%-й интервал уверенности в z-пространстве для ρ задается следующей формулой:

Для r=0.867 и n=859 она даст нижнюю и верхнюю границу соответственно 1.137 и 1.722. В целях их преобразования из z-оценок в r-значения, мы используем следующее обратное уравнение z-преобразования:

Преобразования и интервал уверенности можно вычислить при помощи следующего исходного кода:

В результате получаем 95%-й интервал уверенности для ρ, расположенный между 0.850 и 0.883. Мы можем быть абсолютно уверены в том, что в более широкой популяции олимпийских пловцов существует сильная положительная корреляция между ростом и весом.

Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.

Источник