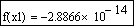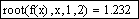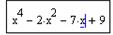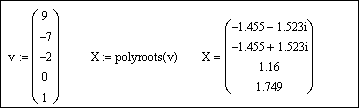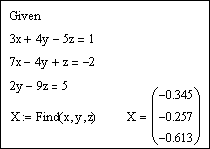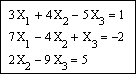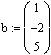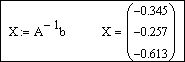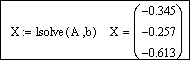Что значит переменная не определена в маткаде

Эта переменная не определена

Вложения

	3.docx (103.2 Кб, 9 просмотров)
	5656.rar (25.8 Кб, 12 просмотров)

Эта переменная не определена
Перепробовал всё, и постоянно выдаёт эту ошибку. Помогите исправить ошибку

Эта переменная не определена
При попытке найти сумму по формуле выскакивает ошибка: эта переменная не определена. Пожалуйсте.

Эта переменная не определена
Здравствуйте! Помогите, пожалуйста! Всё делала по образцу, не соображу, что не так (задание по.

Эта переменная не определена
Добрый день! Вот такая проблема, необходимо из этих 5 уравнений найти Ca,Cb,Cp1,tхл,uхл. Файл и.

У Вас не задано tоб.
Ещё не задано Cv, Kv. Халтура однако!

Добавил недостающие данные, чтобы выходил близкий ответ. Ещё пи пропустили в последнем неравенстве (добавил)!

Эта переменная не определена
Здравствуйте, ребята! Пожалуйста помогите! При решении уравнение в маткаде выходить эта переменная.

Эта переменная не определена
Здравствуйте,выдает ошибку (эта переменная не определена на Т.per) подскажите как исправить.

Эта переменная не определена
Добрый день! Делаю расчет уширения лазерного пучка с помощью системы Галилея, столкнулся с.

Эта переменная не определена
Помогите, какую переменную оно имеет ввиду? Вроде всё же указал.

Эта переменная не определена
Искал по соседним темам, так и не нашёл решения. Mathcad 15 выдаёт ошибку «Эта переменная не.

Эта переменная не определена
Добрый день!Все проверил,и никак разобраться не могу:в чем дело?Помогите,пожалуйста.

Источник

Mathcad find переменная не определена

MathCad | ANSYS CFX | MS Office

Поиск по сайту

Выбор языка

Решение уравнений в MathCad

Часто в курсовом проекте, либо в лабораторной работе встает вопрос о решении какого-либо сложного большого уравнения с одним неизвестным. Не всегда хочется тратить 10 — 20 минут на рутинные преобразования в процессе которых, велика вероятность допущения ошибки. Целесообразно воспользоваться математической программой (в данном случае MathCad), которая быстро и правильно сможет дать ответ. Мы рассмотрим пример использования 2-ух способов решения уравнений, причем как в числах так и в символьном виде.

Способ №1: использование вычислительного блока Given — Find:

Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем первое слово Given. Это служебное слово. Оно «подключает» определенные программные модули mathcad, необходимые для решения уравнения. Эти модули в своем составе содержат основные численные методы решения: метод бисекции, простой итерации и пр. Далее пишется наше уравнение в любом — явном или неявном виде. Само уравнение набирается с клавиатуры с использованием логического символа «равно». На панельке Boolean (Булева алгебра) он выделен жирным шрифтом (см. рис. 1).
Рис. 1. Панель «Булевая алгебра»
Далее пишется слово Find(x) (где х — переменная). Это функция, которая и получает ответ. Функцию Find(x) можно присвоить какой-либо переменной и использовать далее в расчетах. Для получения результата, после Find(x) следует поставить символ «→» либо «=» (см. рис. 2).
Рис. 2. Панель «Вычисления»
В зависимости от сложности уравнения через некоторое время MathCad выведет результат.

Возможности MathCad позволяют определить корень как в численном виде (т. е. результат решения уравнения представляет собой число) так и в символьном (результат — выражение). Для численного определения корня необходимо задать (определить) ВСЕ переменные входящие в уравнение и даже искомую переменную. MathCad воспринимает задание искомой переменной как начальное приближение корня. Крайне важно задаться начальным приближением, поскольку без него корень уравнения невозможно определить в силу особенностей используемых численных методов. Нужно отметить, что некорректное задание начального приближения часто становится причиной получения неверного результата либо его отсутствия вообще. Но не стоит забывать также и о том, что корня может не быть, потому что само уравнение его не имеет.
В том случае, если необходимо решить уравнение относительно какой-либо переменной в символьном виде, то нет необходимости задаваться значениями всех входящих в уравнение параметров и начальным приближением переменной. В этом случае достаточно ввести уравнение (также через «жирное равно») и после оператора Find(x) поставить «→». При этом будут работать уже другие функции MathCad, которые заточены под символьное преобразование и упрощение выражений. Результатом решения будет выражение. Стоит отметить, что MathCad сможет записать решение далеко не всякого уравнения. В этом смысле его возможности ограничены.

Для подтверждения и закрепления выше сказанного, Вам предлагается скачать и познакомиться с примерами решения уравнений как в численном так и в символьном виде.

Пример №1. Решение уравнения в MathCad с помощью блока Given Find численно: Скачать

Пример №2. Решение уравнения в MathCad с помощью блока Given Find символьно: Скачать

Способ №2: Применение метода solve:

Этот метод по существу не отличается от выше рассмотренного, поскольку процедура нахождения корня аналогична. Разница лишь в оформлении. В этом случае наше уравнение записывается без операторов Given и Find. После ввода уравнения на панели Symbolic нажимаем кнопку solve (см. рис. 3), определяем через запятую искомую переменную, жмем «→» и получаем ответ.
Рис. 3. Панель «Символьные»
Иногда, то что не получается найти с помощью Given Find получается в solve.

Пример №3. Решение уравнения в MathCad с помощью solve: Скачать

РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ

4 Решение уравнений и систем средствами Mathcad

Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.

Функция root, блоки Given…Find, Given…Minerr

В ходе численного решения обычно выделяют два этапа:

Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается

root(f(x), x, [a, b])

и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:

Этот прием используется в Mathcad так:

Кроме того, пакет Mathcad имеет встроенную функцию

lsolve(A, b),

Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.

Порядок выполнения лабораторной работы

Лабораторная работа № 4
Решение уравнений и систем в Mathcad.

Задание 1. Решить уравнение .

Решение.

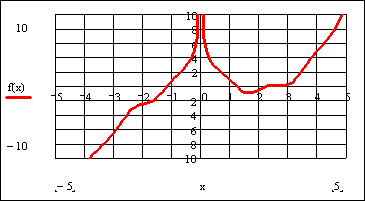
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.

Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:

Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:

Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).

Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).

Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.

После указанных преобразований график функции f(x) будет выглядеть следующим образом:

Этап отделения корней завершен.

Уточним теперь корни уравнения с помощью функции root.

Присвоим начальное приближение переменной x и укажем точность поиска корня:

Уточним заданное приближение к значению корня с помощью функции root:

Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:

Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:

Задание 2. Решить уравнение .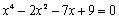

Решение.

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:

Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.

Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.

Для получения результата напечатаем polyroots(v) =:

Задание 3. Решить систему линейных уравнений 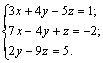Сделать проверку.

Решение.

1-й способ. Использование блока Given … Find.

Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:

Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).

После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:

Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом

После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.

2-й способ. Использование блока Given…Minerr.

Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:

3-й способ. Решение системы линейных уравнений матричным способом.

Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:

Решим систему матричным способом по формуле

Решим систему с помощью функции lsolve:

Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:

программирование mathcad скалярный трехмерный

Функция Find (Найти) работает в ключевой связке с ключевым словом Given (Дано). Конструкция Given — Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.

Если задано уравнение f(x) = 0, то его можно решить следующим образом с помощью блока Given — Find:

— задать начальное приближение

— ввести служебное слово

В результате после знака равно выведется найденный корень.

Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.

В Mathcad можно писать программы двух видов

Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вы0числениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.

Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT).

Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.

Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»).

Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.

Программа содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.

Источник

При решении следующей задачи (Скриншот 1) получаю ошибку «эта переменная не определена», но только для функции Minimize, тогда как Maximize работает корректно. Уже не единожды проверил ввод условий, нигде ошибки не вижу, помогите разобраться пожалуйста. Во вложения прикладываю архив с маткадовским файлом.

Вложения

znnL4.rar (7.8 Кб, 7 просмотров)

При попытке воспользоваться функцией Minimize ошибка: переменная не определена
Здравствуйте. Пытаюсь решить контрольную в mathcadе, на последней строке ошибка, в функции.

Эта переменная не определена
Добрый день! Делаю расчет уширения лазерного пучка с помощью системы Галилея, столкнулся с.

Эта переменная не определена
Нужна помощь, в MathCad буквально день Помогите разобраться Ввожу данные, потом уравнение Не.

Решение

Эта переменная не определена
Всем, привет. Я оочень начинающий пользователь проги, надо лабу сделать) помогите плиз(( не считает.

Эта переменная не определена
Искал по соседним темам, так и не нашёл решения. Mathcad 15 выдаёт ошибку «Эта переменная не.

Эта переменная не определена
Перепробовал всё, и постоянно выдаёт эту ошибку. Помогите исправить ошибку

Эта переменная не определена
Добрый день! Вот такая проблема, необходимо из этих 5 уравнений найти Ca,Cb,Cp1,tхл,uхл. Файл и.

Эта переменная не определена
При попытке найти сумму по формуле выскакивает ошибка: эта переменная не определена. Пожалуйсте.

Эта переменная не определена
Уважаемые форумчане, подскажите пожалуйста, в чём ошибка?( Ошибка: Эта переменная не определена.

Источник