Что значит параллельно плоскости
Параллельные плоскости, признак и условия параллельности плоскостей
В данной статье будут изучены вопросы параллельности плоскостей. Дадим определение плоскостям, которые параллельны между собой; обозначим признаки и достаточные условия параллельности; рассмотрим теорию на иллюстрациях и практических примерах.
Параллельные плоскости: основные сведения
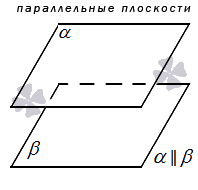
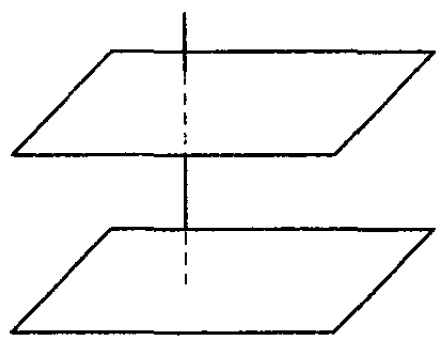
Параллельные плоскости – плоскости, не имеющие общих точек.
На чертеже, как правило, плоскости, параллельные друг другу, отображаются как два равных параллелограмма, имеющих смещение относительно друг друга.
Параллельность плоскостей: признак и условия параллельности
В процессе решения геометрических задач зачастую возникает вопрос: а параллельны ли заданные плоскости между собой? Для получения ответа на этот вопрос используют признак параллельности, который также является достаточным условием параллельности плоскостей. Запишем его как теорему.
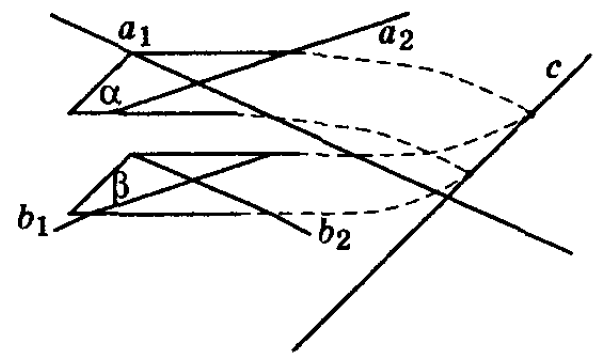
Плоскости являются параллельными, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
В практике для доказательства параллельности, в том числе, применяют две следующие теоремы.
Если одна из параллельных плоскостей параллельна третьей плоскости, то другая плоскость или также параллельна этой плоскости, или совпадает с ней.
Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.
На основе этих теорем и самого признака параллельности доказывается факт параллельности любых двух плоскостей.
Для параллельности заданных плоскостей α и β необходимо и достаточно, чтобы система линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имела решения (являлась несовместной).
Предположим, что заданные плоскости, определяемые уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 являются параллельными, а значит не имеют общих точек. Таким образом, не существует ни одной точки в прямоугольной системе координат трехмерного пространства, координаты которой отвечали бы условиям одновременно обоих уравнений плоскостей, т.е. система A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имеет решения. Если указанная система не имеет решений, тогда не существует ни одной точки в прямоугольной системе координат трехмерного пространства, чьи координаты одновременно отвечали бы условиям обоих уравнений системы. Следовательно, плоскости, заданные уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 не имеют ни одной общей точки, т.е. они параллельны.
Разберем использование необходимого и достаточного условия параллельности плоскостей.
Решение
Запишем систему уравнений из заданных условий:
Проверим, возможно ли решить полученную систему линейных уравнений.
Отметим, что, если бы мы применили для решения системы линейных уравнений метод Гаусса, это дало бы тот же результат.
Ответ: заданные плоскости параллельны.
Необходимое и достаточное условие параллельности плоскостей возможно описать по-другому.
Чтобы две несовпадающие плоскости α и β были параллельны друг другу необходимо и достаточно, чтобы нормальные векторы плоскостей α и β являлись коллинеарными.
Доказательство сформулированного условия базируется на определении нормального вектора плоскости.
n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2
Решение
Для получения координат нормального вектора плоскости x 12 + y 3 2 + z 4 = 1 приведем это уравнение к общему уравнению плоскости:
Ответ: плоскости α и β не совпадают; их нормальные векторы коллинеарные. Таким образом, плоскости α и β параллельны.
Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости.
В этой статье всесторонне раскрыта тема «параллельность прямой и плоскости». Сначала дано определение параллельных прямой и плоскости, приведена графическая иллюстрация и пример. Далее сформулирован признак параллельности прямой и плоскости, а также озвучены необходимые и достаточные условия параллельности прямой и плоскости. В заключении приведены развернутые решения задач, в которых доказывается параллельность прямой и плоскости.
Навигация по странице.
Параллельные прямая и плоскость – основные сведения.
Начнем с определения параллельных прямой и плоскости.
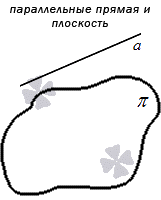
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Для обозначения параллельности используется символ «
». То есть, если прямая a и плоскость 
параллельны, то можно кратко записать a .
Заметим, что выражения «прямая a и плоскость параллельны», «прямая a параллельна плоскости » и «плоскость параллельна прямой a » одинаково употребимы.
В качестве примера параллельных прямой и плоскости приведем натянутую гитарную струну и плоскость грифа этой гитары.
Параллельность прямой и плоскости далеко не всегда является очевидным фактом. Другими словами, параллельность прямой и плоскости приходится доказывать. Существует достаточное условие, выполнение которого гарантирует параллельность прямой и плоскости. Это условие называют признаком параллельности прямой и плоскости. Прежде чем ознакомиться с формулировкой этого признака, рекомендуем повторить определение параллельных прямых.
Озвучим еще одну теорему, которую можно использовать для установления параллельности прямой и плоскости.
Если одна из двух параллельных прямых параллельна некоторой плоскости, то вторая прямая либо также параллельна этой плоскости, либо лежит в ней.
Определение направляющего вектора прямой и определение нормального вектора плоскости позволяют записать необходимое и достаточное условие параллельности прямой и плоскости.
Это условие удобно использовать для доказательства параллельности прямой и плоскости, которые заданы в прямоугольной системе координат в трехмерном пространстве некоторыми уравнениями.
Разберем решения нескольких примеров.
Являются ли прямая 
и плоскость 
параллельными?
Заданная прямая не лежит в плоскости, так как координаты точки прямой 
не удовлетворяют уравнению плоскости: 
. Проверим выполнение необходимого и достаточного условия параллельности прямой и плоскости. Очевидно, 
— направляющий вектор прямой , 
— нормальный вектор плоскости . Вычислим скалярное произведение векторов 
и 
: 
. Таким образом, векторы и перпендикулярны. Следовательно, заданные прямая и плоскость параллельны.
да, прямая и плоскость параллельны.
Нормальным вектором плоскости Oyz является вектор 
. В качестве направляющего вектора прямой AB возьмем вектор 
. Координаты точек начала и конца вектора позволяют вычислить координаты этого вектора, тогда 
. Проверим выполнение необходимого и достаточного условия перпендикулярности векторов и : 
. Следовательно, прямая AB и координатная плоскость Oyz не параллельны.
нет, не параллельны.
Разобранное условие не совсем удобно для доказательства параллельности прямой a и плоскости , так как отдельно приходится проверять, что прямая a не лежит в плоскости . Поэтому, доказывать параллельность прямой a и плоскости удобнее с помощью следующего необходимого и достаточного условия.
Пусть прямая a задана уравнениями двух пересекающихся плоскостей 
,
а плоскость — общим уравнением плоскости 
.
Для параллельности прямой a и плоскости необходимо и достаточно, чтобы система линейных уравнений вида 
не имела решений.
В свою очередь система уравнений не имеет решений, когда ранг основной матрицы системы меньше ранга расширенной матрицы (это следует из теоремы Кронекера-Капелли, при необходимости смотрите статью решение систем линейных уравнений). Несовместность этой системы уравнений можно также показать, используя метод Гаусса для решения систем линейных уравнений.
Докажите параллельность прямой 
и плоскости 
.
Перейдем от канонических уравнений прямой к уравнениям двух пересекающихся плоскостей:
Для доказательства параллельности прямой 
и плоскости покажем, что система уравнений 
не имеет решения. Воспользуемся методом Гаусса:
Действительно, система уравнений несовместна, следовательно, заданные прямая и плоскость не имеют общих точек. Этим доказана параллельность прямой и плоскости .
Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости
Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.
Параллельные прямые и плоскость – основные сведения
Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.
Параллельность прямой и плоскости – признак и условия параллельности
Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.
Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.
Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.
Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.
Значит, перпендикулярность векторов a → и n → очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.
Ответ: прямая с плоскостью параллельны.
Отсюда следует, что прямая А В с координатной плоскостью О y z не являются параллельными.
Ответ: не параллельны.
Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат О х у z не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:
Система уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.
Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:
Видим, что она не решаема, значит прибегнем к методу Гаусса.
Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.
Ответ: прямая и плоскость параллельны.
Параллельность плоскостей
Содержание
Классическое определение
Две плоскости называются параллельными, если они не имеют общих точек.
Свойства и признаки
Аналитическое определение
и 
параллельны, то нормальные векторы 
и 
коллинеарны (и обратно). Поэтому условие
[1] есть необходимое и достаточное условие параллельности или совпадения.
Пример 1
Плоскости 
и 
параллельны, так как 
Пример 2
Плоскости 
и 
непараллельны так как 
, а 
Замечание. Если не только коэффициенты при координатах, но и свободные члены пропорциональны, то есть если
[2] то плоскости совпадают. Так уравнения 
и 
представляют одну и ту же плоскость.
Примечания
Полезное
Смотреть что такое «Параллельность плоскостей» в других словарях:
Параллельность — отношение между прямыми. Определяется немного по разному в различных разделах геометрии. Содержание 1 В евклидовой геометрии 1.1 Свойства … Википедия
ПАРАЛЛЕЛЬНОСТЬ — 1) равное отстояние: такое положение линий или плоскостей, при котором они отстоят во всех точках одинако одна от другой. 2) сходство, напр. некоторых отдельных мест в Св. Писании. Словарь иностранных слов, вошедших в состав русского языка.… … Словарь иностранных слов русского языка
Параллельность осей вращения шпинделей — 2.6. Параллельность осей вращения шпинделей Допуск на расстоянии L = 150 мм 25 мкм. Параллельность осей вращения шпинделей рассчитывают по результатам измерения перпендикулярности (параллельности) шпинделей относительно измерительной базы по пп.… … Словарь-справочник терминов нормативно-технической документации
Параллельность линии центров делительной головки направляющим хобота в вертикальной и горизонтальной плоскостях — 3.3.4. Параллельность линии центров делительной головки направляющим хобота в вертикальной и горизонтальной плоскостях Черт. 44 Допуск, мкм, для станков с конусом шпинделя Морзе до 5 на длине L = 150 мм для головок классов точности: П … Словарь-справочник терминов нормативно-технической документации
Параллельность направляющих хобота оси вращения шпинделя в вертикальной и горизонтальной плоскостях — 1.15. Параллельность направляющих хобота оси вращения шпинделя в вертикальной и горизонтальной плоскостях Черт. 17 Допуск, мкм, на длине перемещения L = 150 мм для станков классов точности: П. 12 В … Словарь-справочник терминов нормативно-технической документации
ГОСТ 26016-83: Станки фрезерные широкоуниверсальные инструментальные. Нормы точности — Терминология ГОСТ 26016 83: Станки фрезерные широкоуниверсальные инструментальные. Нормы точности оригинал документа: 1.8. Взаимная перпендикулярность продольного перемещения вертикального стола направлению перемещения шпиндельной бабки Черт. 9… … Словарь-справочник терминов нормативно-технической документации
N-мерная евклидова геометрия — N мерная евклидова геометрия обобщение евклидовой геометрии на пространство большего числа измерений. Хотя физическое пространство является трёхмерным[1], и человеческие органы чувств рассчитаны на восприятие трёх измерений[2], N мерная… … Википедия
ГОСТ 2110-93: Станки расточные горизонтальные с крестовым столом. Нормы точности — Терминология ГОСТ 2110 93: Станки расточные горизонтальные с крестовым столом. Нормы точности оригинал документа: 4.18 Круглость: а) отверстия d1; б) поверхности 5 … Словарь-справочник терминов нормативно-технической документации
ГОСТ 30027-93: Модули гибкие производственные и станки многоцелевые сверлильно-фрезерно-расточные. Нормы точности — Терминология ГОСТ 30027 93: Модули гибкие производственные и станки многоцелевые сверлильно фрезерно расточные. Нормы точности оригинал документа: 4.10 Круглость: а) отверстия d1; б) поверхности 5 … Словарь-справочник терминов нормативно-технической документации
ПАРАЛЛЕЛИЗМ — 1) сравнительное сопоставление каких либо предметов или вопросов; 2) то же, что параллельность, см. ПАРАЛЛЕЛЬНЫЕ ЛИНИИ. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907. ПАРАЛЛЕЛИЗМ Сравнит, сопоставление каких… … Словарь иностранных слов русского языка
Инструменты пользователя
Инструменты сайта
Боковая панель
Стереометрия:
Контакты
Содержание
Параллельность прямых и плоскостей
Прямые
Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Лемма о пересечении плоскости параллельными прямыми. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Прямая и плоскость
Три случая взаимного расположения прямой и плоскости в пространстве:
Прямая и плоскость называются параллельными, если они не имеют общих точек.
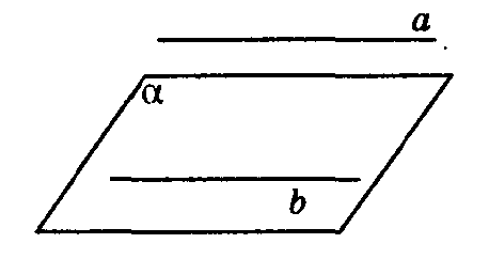
Признак параллельности прямой и плоскости:
Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельно данной плоскости. См.Рис.1.
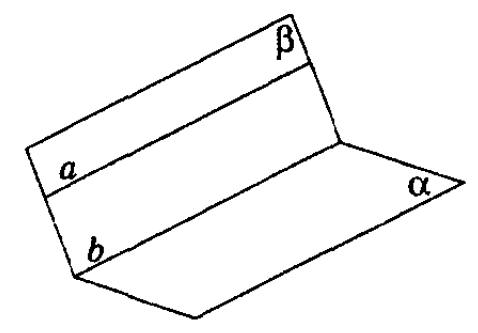
Свойство прямой, параллельной плоскости:
Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей. См.Рис.2.
Плоскости
Параллельные плоскости – плоскости, не имеющие общих точек.
Признаки параллельности плоскостей:
Свойства параллельных плоскостей: