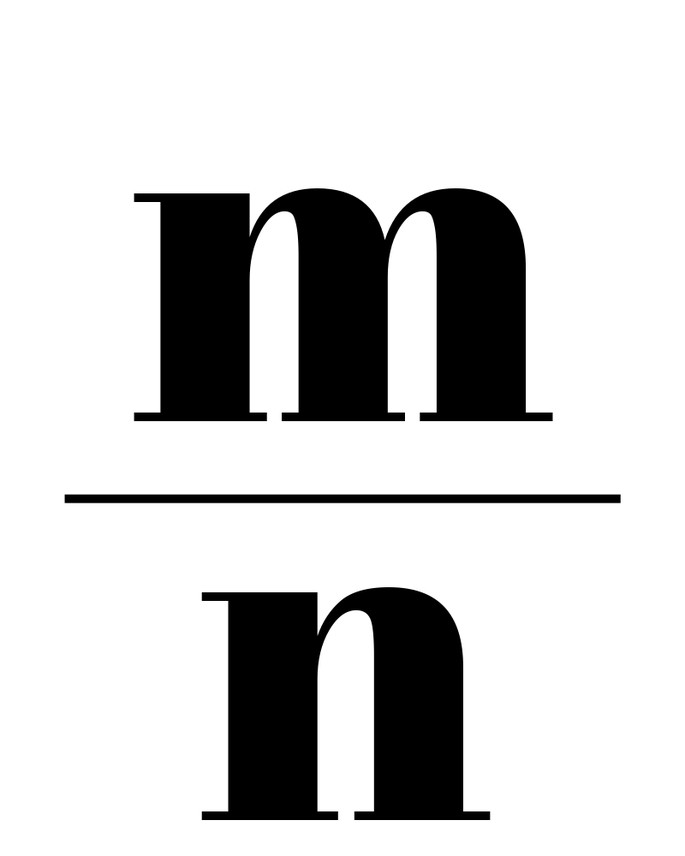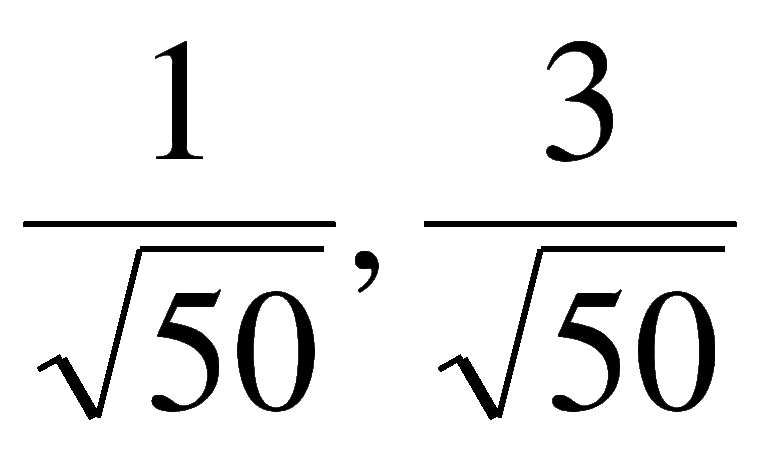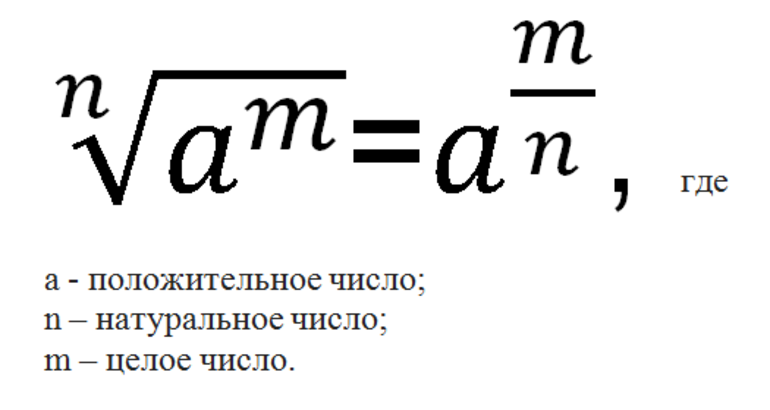Что значит отрицательные иррациональные числа
Иррациональные числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение иррациональных чисел
Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби:
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.
Примеры иррациональных чисел:
Множество иррациональных чисел договорились обозначать латинской буквой I.
Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.
Свойства иррациональных чисел
Какие числа являются иррациональными мы уже поняли, но это еще не все. Есть еще важная тема для изучения: их основные свойства.
Свойства иррациональных чисел:
Определение рациональных чисел
А теперь наоборот: рассмотрим противоположное заданной теме определение.
Рациональное число — это такое число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или нуля. Если число можно получить делением двух целых чисел — это число точно рациональное.
Рациональные числа — это те, которые можно представить в виде:
где числитель m — целое число, а знаменатель n — натуральное число.
Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Множество рациональных чисел принято обозначать латинской буквой Q.
Примеры рациональных чисел:
У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.
Основные свойства действий с рациональными числами
Полный текст книги в PDF одним файлом:
В нашем арсенале инструментов появились замечательные лабораторные весы. Для работы с массами требуется только эталон-масса, наличие шкалы упрощает измерение длин. И наша работа по продолжению классифицированию остальных масс (чисел), должна быть упрощена. Однако столкнулись с неприятностью. Мы нашли «необычный» камень, положив который в правую чашу на эталон-расстояние, невозможно найти методом 3НТТ тождественное расстояние эталону-массе слева.
Мы долго размышляем. Наконец, нас осенило. Со словами «Эврика!» продолжаем эксперимент.
– А что, если левую чашу двигать и по правой части шкалы? Может это что-то даст?
Действительно, переместив левую чашу на расстоянии «A» вправо, методом 3НТТ удалось получить тождество чисел.
Удивительное свойство некоторых камней – наличие двух камней по одну сторону весов уравновешивает отсутствие масс по другую сторону.
Экспериментируя, мы нашли другой интересный камень из кучи рациональных камней – присутствие его вместе с «необычным» камнем в одной чаше никак не влияет на результат любого взвешивания.
Примечательным является то, что он уже нами чётко обозначен конкретным числовым значением, в отличие от «необычного» камня. Ничего не поменяется, если поменять «обычный» камень на «необычный», расположив чашу по другую сторону опоры на тождественном расстоянии. Либо наоборот. Вот и вся разница.
Назовём «необычный» камень – отрицательным. Число «A», тождественное ему – отрицательное число. Отрицательное число – не означает «плохое» число. Все числа хорошие, просто на все свойства чисел не хватает «хороших» названий. Символ для обозначения отрицательности – «–A».
Особое качество отрицательного камня можно указать на весах: стрелка массы-пробы вниз – обычное число, вверх – число отрицательное. Чтобы как-то различать стрелки вверх-вниз, на весах укажем направление «правильных» чисел. Логично было бы указать стрелку вниз, но история распорядилась иначе: общепринятым стало указание вверх.
С расстояниями проще: они указывают «правильное» направление – вправо. Шкалу расстояний обозначим OX. Эту ось называют – абсцисса. Шкала масс обозначается осью OY – это ордината.
Оси направлений, масштаб (эталон), точка опоры (ноль) называются координатной плоскостью.
Однажды нам попался камень «A» и ветка «B»,у которых масса и длина тождественны (A=B). В тождестве мы убедились, положив массу «A» на эталонном расстоянии с одной стороны весов, на другую – эталон «1» на расстоянии «B».
Это ещё не всё. Так же было тождество массе «2», когда по другую сторону на расстоянии «B» лежала масса «A».
Необычность была в невозможности найти тождественную массу массе «A» – она была либо больше, либо меньше, пронумерованной кучи камней. Это же относилось к расстоянию «B».
Записать данное соотношение можно так: «A*A=1*2». По-другому: A;=2, либо A=;2.
Чтобы представить число «A» рациональным числом нам не хватает цифр: 1.41421356237… – это малая часть того, что нами получено.
Что значит отрицательные иррациональные числа
Множество иррациональных чисел обычно обозначается заглавной латинской буквой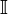 
в полужирном начертании без заливки. Таким образом: 
, т.е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.
О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа 
.
Свойства
Примеры
Примеры доказательства иррациональности
Корень из 2
Допустим противное: 
рационален, то есть представляется в виде несократимой дроби 
, где 
— целое число, а 
— натуральное число. Возведём предполагаемое равенство в квадрат:
.
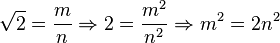
Отсюда следует, что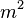 
чётно, значит, чётно и . Пускай 
, где 
целое. Тогда
Следовательно, 
чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.
Двоичный логарифм числа 3
Допустим противное: 
рационален, то есть представляется в виде дроби , где и — целые числа. Поскольку 0″ src=»http://upload.wikimedia.org/math/d/1/3/d1351d4222403731e31419faebbe54bc.png» />, и могут быть выбраны положительными. Тогда
Но 
чётно, а 
нечётно. Получаем противоречие.
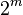
История
Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. — ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены.
Первое доказательство существования иррациональных чисел обычно приписывается Гиппасу из Метапонта (ок. 500 гг. до н. э.), пифагорейцу, который нашёл это доказательство, изучая длины сторон пентаграммы. Во времена пифагорейцев считалось, что существует единая единица длины, достаточно малая и неделимая, которая целое число раз входит в любой отрезок. Однако Гиппас обосновал, что не существует единой единицы длины, поскольку предположение о её существовании приводит к противоречию. Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число должно быть одновременно и четным, и нечетным. Доказательство выглядело следующим образом:
Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.
Феодор Киренский доказал иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17. По поводу того, каким могло быть это доказательство, историками математики было высказано несколько различных предположений. Согласно наиболее правдоподобному предположению Жана Итара (1961), оно было основано на пифагорейской теории чётных и нечётных чисел, в том числе — на теореме о том, что нечётное квадратное число за вычетом единицы делится на восемь треугольных чисел.
Позже Евдокс Книдский (410 или 408 г. до н. э. — 355 или 347 г. до н. э.) развил теорию пропорций, которая принимала во внимание как рациональные, так и иррациональные отношения. Это послужило основанием для понимания фундаментальной сути иррациональных чисел. Величина стала считаться не числом, но обозначением сущностей, таких как отрезки прямых, углы, площади, объёмы, промежутки времени — сущностей, которые могут меняться непрерывно (в современном понимании этого слова). Величины были противопоставлены числам, которые могут меняться лишь «прыжками» от одного числа к соседнему, например, с 4 на 5. Числа составляются из наименьшей неделимой величины, в то время как величины можно уменьшать бесконечно.
Поскольку никакое количественное значение не сопоставлялось величине, Евдокс смог охватить и соизмеримые, и несоизмеримые величины при определении дроби как отношения двух величин, и пропорции как равенства двух дробей. Убрав из уравнений количественные значения (числа), он избежал ловушки, состоящей в необходимости назвать иррациональную величину числом. Теория Евдокса позволила греческим математикам совершить невероятный прогресс в геометрии, предоставив им необходимое логическое обоснование для работы с несоизмеримыми величинами. «Книга 10 Элементов» Евклида посвящена классификации иррациональных величин.
Средние века
Средние века ознаменовались принятием таких понятий как ноль, отрицательные числа, целые и дробные числа, сперва индийскими, затем китайскими математиками. Позже присоединились арабские математики, которые первыми стали считать отрицательные числа алгебраическими объектами (наряду и на равных правах с положительными числами), что позволило развить дисциплину, ныне называемую алгеброй.
Арабские математики соединили древнегреческие понятия «числа» и «величины» в единую, более общую идею вещественных чисел. Они критически относились к представлениям Евклида об отношениях, в противовес ей они развили теорию отношений произвольных величин и расширили понятие числа до отношений непрерывных величин. В своих комментариях на Книгу 10 Элементов Евклида, персидский математик Аль Махани (ок 800 гг. н. э.) исследовал и классифицировал квадратичные иррациональные числа (числа вида) и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами. Он легко оперировал этими объектами, но рассуждал как об обособленных объектах, например:
 | Рациональной [величиной] является, например, 10, 12, 3%, 6% и так далее, поскольку эти величины произнесены и выражены количественно. Что не рационально, то иррационально, и невозможно произнести или представить соответствующую величину количественно. Например, квадратные корни чисел таких так 10, 15, 20 — не являющихся квадратами. |  |
В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни — иррациональными. Он также ввел арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин:
| результат сложения иррациональной величины и рациональной, результат вычитания рациональной величины из иррациональной, результат вычитания иррациональной величины из рациональной. | |
Египетский математик Абу Камил (ок. 850 г. н. э. — ок. 930 г. н. э.) был первым, кто счел приемлемым признать иррациональные числа решением квадратных уравнений или коэффициентами в уравнениях — в основном, в виде квадратных или кубических корней, а также корней четвёртой степени. В X веке иракский математик Аль Хашими вывел общие доказательства (а не наглядные геометрические демонстрации) иррациональности произведения, частного и результатов иных математических преобразований над иррациональными и рациональными числами. Ал Хазин (900 г. н. э. — 971 г. н. э.) приводит следующее определение рациональной и иррациональной величины:
| Пусть единична величина содержится в данной величине один или несколько раз, тогда эта [данная] величина соответствует целому числу… Каждая величина, которая составляет половину, или треть, или четверть единичной величины, или, сравненная с единичной величиной составляет три пятых от нее, это рациональная величина. И в целом, всякая величина, которая относится к единичной как одно число к другому, является рациональной. Если же величина не может быть представлена как несколько или часть (l/n), или несколько частей (m/n) единичной длины, она иррациональная, то есть невыразимая иначе как с помощью корней. | |
Многие из этих идей были позже переняты европейскими математиками после перевода на латынь арабских текстов в XII веке. Аль Хассар, арабский математик из Магриба, специализировавшийся на исламских законах о наследстве, в XII веке ввел современную символьную математическую нотацию для дробей, разделив числитель и знаменатель горизонтальной чертой. Та же нотация появилась затем в работах Фибоначчи в XIII веке. В течение XIV—XVI вв. Мадхава из Сангамаграмы и представители Керальской школы астрономии и математики исследовали бесконечные ряды, сходящиеся к некоторым иррациональным числам, например, к π, а также показали иррациональность некоторых тригонометрических функций. Джестадева привел эти результаты в книге Йуктибхаза.
Наше время
В XVII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667—1754) и Леонард Эйлер (1707—1783). Когда теория комплексных чисел в XIX веке стала замкнутой и чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные (доказав при этом существование трансцендентных чисел), тем самым переосмыслив работы Евклида по классификации иррациональных чисел. По этой теме в 1872 были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ начал рассмотрения, схожие с Гейне, именно 1872 год принято считать годом рождения теории. Вейерштрасс, Кантор и Гейне обосновывали свои теории при помощи бесконечных рядов, в то время как Дедекинд работал с (ныне так называемым) Дедекиндовым сечением множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.
Цепные дроби, тесно связанные с иррациональными числами (цепная дробь, представляющая данное число, бесконечна тогда и только тогда, когда число является иррациональным), были впервые исследованы Катальди в 1613 году, затем снова привлекли к себе внимание в работах Эйлера, а в начале XIX века — в работах Лагранжа. Дирихле также внёс значительный вклад в развитие теории цепных дробей.
История открытия
Одни учёные считают, что иррациональные числа были открыты Пифагором. Другие полагают, что существование таких величин было выявлено пифагорейцами в V веке до нашей эры. Третьи выдвигают версию, что открытие принадлежит древним учёным Азии.
Несмотря на то что возникновение нового типа чисел связывают с именем Пифагора, сам великий учёный этих величин не признавал. Математик основывал свои труды на рациональности значений, а потому их иные виды были неприменимы к его теориям. Из-за огромного авторитета учёного иррациональные значения стали использоваться в науке только после его смерти.
Аристотель доказал иррациональность квадратного корня из 2. Теодор из Кирены привёл подобные доказательства в отношении корня из 3, 5 и так далее. Есть версия, что даже термины для соответствующей теории ввёл этот математик. Его ученик Теэтет на основании указанных данных создал общее учение об иррациональности. Полная теория иррациональных количественных значений Эвклид изложил в пятой книге «Начал».
Понятие и характеристика
Огромным прорывом в математической науке стали числа, которые называются иррациональными. Какие-либо ограничения, связанные с целыми величинами или обыкновенными дробями, были сняты. Люди получили возможность открывать и даже изобретать новые количественные значения.
Иррациональным считается вещественное число, не являющееся рациональным. Оно не может быть представлено в виде арифметической дроби n/m, где числитель и знаменатель являются целыми величинами, а n не равно 0. Также подобные значения невозможно точно выразить целой величиной. Это значит, что иррациональные числа всегда выглядят, как бесконечные непериодические десятичные дроби. Для их обозначения применяют радикалы или специальные буквы, например, е, π. Множество чисел обозначается заглавной буквой в полужирном начертании без заливки.
В геометрии оно представляется в качестве отрезка, длина которого несоизмерима с единичной. Об этой несоизмеримости упоминали и древние математики. Они установили, что диагональ квадрата не имеет общей меры с его стороной, что равносильно иррациональности корня из 2.
Не всякая величина из множества значений, не относящихся к рациональным, так известна, как число π. В школьной программе его часто определяют, как 3,14, но истинный показатель π значительно ближе к 3. Следует отметить, что даже известная длинная десятичная дробь является лишь приближённым вариантом, поскольку указанное число нельзя точно установить. Дробь, которую используют для этого, бесконечна, а цифры в ней распределяются без какой-либо закономерности.
Самыми известными примерами таких иррациональных чисел являются:
Математиками составлены специальные таблицы величин, не являющихся рациональными. Но так как множество бесконечно, определить тип значения по данным таблицам довольно сложно.
Зачастую понять, что число иррационально, можно по его соответствию одному из перечисленных признаков:
Но в ряде случаев установить иррациональность значения возможно только посредством доказательства. К примеру, школьникам часто дают задание доказать, что число log3 4 не относится к рациональным.
Отличительные качества
Значения, которые нельзя выразить дробью, существенно отличаются от других чисел. К их уникальным свойствам относятся следующие:
Виды преобразования выражений
Иррациональные выражения содержат операцию извлечения корня. Это особые записи, состоящие из радикалов и знаков алгебраических действий.
Во время преобразования таких выражений нельзя допускать сужения области допустимых значений. С ними разрешается проводить любые из основных тождественных преобразований:
В основе подобного упрощения выражений лежат действия, общие для всех количественных значений. Поэтому в процессе преобразования этих записей необходимо сохранять установленный порядок выполнения действий.
Замена исходной записи
Подкоренное выражение можно заменить тождественно равным, то есть математической записью, значение которой будет равно исходному. Следует учитывать, что равенство должно соблюдаться при любых допустимых значениях переменных, которые входят в состав обоих выражений.
Это утверждение основывается на единственности корня из числа. Иными словами, нет значения, которое, отличаясь от исходной величины, сохраняло бы равенство с нею.
Использование свойств корней
Для упрощения сложных выражений часто применяются свойства корней, к примеру, перемножение их степеней. Делать это необходимо в соответствии со специальными формулами.
Особое внимание при работе следует обращать на отрицательные числа и выражения с переменными. В ряде случаев для применения формул такие значения сначала придётся привести к тождественно равным, которые подойдут для дальнейшего использования свойств корней.
Внесение множителя под знак корня — это преобразование произведения, в котором лишь один из множителей находится под знаком радикала со степенью, выраженной натуральным числом. После замены выражения под корнем будут находиться все множители, составляющие произведение, но оно останется равным исходному.
Обратным изменением является вынесение множителя из-под радикала. Его используют в случаях, когда степень корня равна степени множителя под радикалом. В таких ситуациях указанный множитель можно извлечь и тем самым упростить выражение.
Изменение дробей
Иррациональные математические записи могут содержать дроби с радикалами в делимом или делителе. С ними разрешается проводить любые действия, относящиеся к основным преобразованиям дробных чисел:
Избавление от иррациональности в знаменателе
Освобождение от иррациональности в знаменателе представляет собой преобразование дроби путём её замены на тождественно равную с делителем, не содержащим корней и степеней. Для этого необходимо последовательно провести два действия:
Переход к степеням
Переход от радикалов к степеням осуществляется на основе равенства, давшего определение степени, которая имеет рациональный показатель. При этом используется следующая формула:
Если же величина под радикалом отрицательная или там находится выражение с переменными, то перед использованием формулы подкоренное значение необходимо преобразовать. Для этого следует применять свойства степеней.
Математические действия
Иррациональные выражения записывают друг за другом с сохранением знаков и лишь после этого складывают или вычитают. Иногда их преобразуют в подобные, то есть имеющие одинаковые подкоренные значения, а затем проводят арифметические действия.
Чтобы найти произведение выражений с одинаковыми радикалами, умножают значения, находящиеся под знаком корня. Полученный результат вносится под корень изначальных выражений.
При делении степени корней делимого и делителя также должны быть равны. Если это условие соблюдено, то первое выражение делится на второе, после чего итог действия записывается под исходный знак радикала.
Правила сравнения
Иногда для решения математических задач необходимо провести сравнение иррациональных значений. При этом необходимо руководствоваться следующими правилами:
Для возведения иррациональной величины в степень необходимо возвести в неё значение под радикалом. Если величина корня равна степени, то в итоге число или выражение выносится из-под корня неизменным, поскольку возникают взаимно сокращающиеся действия.
Если иррациональное выражение находится под корнем, то для его извлечения показатели радикалов умножают. Этот метод позволяет упрощать извлечение корней четвёртой, шестой, восьмой, девятой степени.
Иррациональные числа можно узнать по специальным буквам, используемым для их обозначения, или по написанию в виде десятичных дробей, не имеющих окончания. Выражения этого типа легко отличить по наличию радикала. С подобными значениями проводят те же действия, что и с другими вещественными числами. Их можно умножить, сложить, сравнить и так далее.