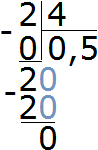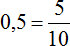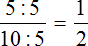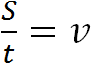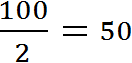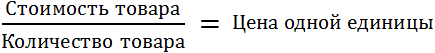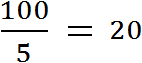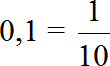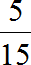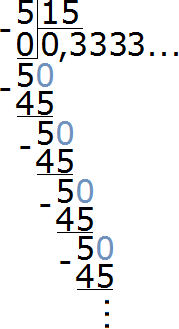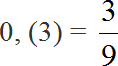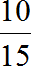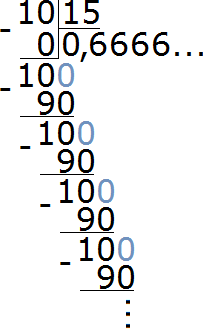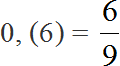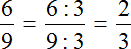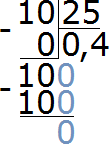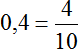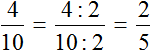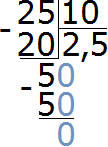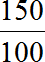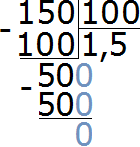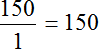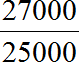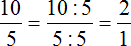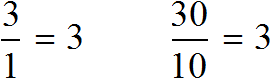Что значит относится как
Значение слова «относиться»
2. Входить в состав, в разряд, в число кого-, чего-л. Относиться к классу млекопитающих. Относиться к людям какого-л. склада.
3. к кому-чему и ( устар.) до кого-чего. Иметь отношение (в 3 знач.) к кому-, чему-л., касаться кого-, чего-л. По возвращении моем напечатал я стихотворение, не относившееся ко взятию Арзрума. Пушкин, Путешествие в Арзрум (ранняя редакция). — Как мне не знать-с всего, что до вашего семейства относится? Тургенев, Дворянское гнездо. В Петрозаводске я засел в архивах и библиотеке и начал читать все, что относилось к Петровскому заводу. Паустовский, Золотая роза. || Быть обращенным к кому-л., предназначенным для кого-л. Молодая девушка, к которой относилось это восклицание, остановилась. Тургенев, Накануне. Я не понял, к кому относилось это приветствие, но невольно привстал и сказал: — Здравствуйте. Чаковский, Это было в Ленинграде.
4. Находиться в каком-л. соответствии, соотношении с чем-л.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
относи́ться
1. иметь определённое мнение, представление о чём-либо ◆ Я ко всему такому отношусь с юмором и радуюсь, если ко мне так же относятся мои друзья, знакомые. «Вы над собой смеяться не боитесь?», 2002 г. // «»Дело» (Самара)» (цитата из НКРЯ)
2. обращаться с кем-либо, реагировать на что-либо определённым образом ◆ К нему там относились с уважением.
3. иметь к чему-либо касательство, быть причастным ◆ Это к делу не относится.
4. быть частью какого-либо множества, класса ◆ К хищным жукам относятся и плавунцы. А. Л. Калуцкий, «Отряд Жуки», 2003 г. // «Биология» (цитата из НКРЯ)
5. матем. то же, что соотноситься, составлять определённую пропорцию ◆ Если взять полусферу на плоскости, то периметр её основания будет относиться к высоте как 2π.
6. страдат. к относить ◆ Каждый день эти вещи относятся в ту комнату.
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: отъесться — это что-то нейтральное, положительное или отрицательное?
Словари
1. Проявлять определённый характер обращения при общении с кем-либо или при соприкосновении с чем-либо.
2. Проявлять свое мнение о чём-либо.
II сов. неперех. разг.
1. Утратить возможность носиться вследствие ветхости; износиться (об одежде, обуви).
1. Входить в состав, в разряд каких-либо явлений, предметов.
Морфология: я отношу́сь, ты отно́сишься, он/она/оно отно́сится, мы отно́симся, вы отно́ситесь, они отно́сятся, относи́сь, относи́тесь, относи́лся, относи́лась, относи́лось, относи́лись, относя́щийся, относи́вшийся, относя́сь; св. отнести́сь
1. Если какое-либо событие, явление, проблема и т. п. относятся к чему-либо или кому-либо, значит, они связаны с ними.
Его творчество относится непосредственно к нашему времени, являясь синтезом романтизма и технологии.
2. Когда какая-либо собственность, какой-либо объект относятся к кому-либо, чему-либо, значит, они ему принадлежат или подведомственны.
Женский Горненский монастырь в Иерусалиме относится к Московской патриархии.
3. Когда ваши слова, мнение и т. п. относятся к чему-либо или кому-либо, значит, они обращены к ним, имеют их в виду.
Всё сказанное относится в особенности к промышленному использованию электроэнергии. | Мои слова прежде всего относятся к начинающим журналистам.
4. Когда человек или предмет относятся к числу, разряду каких-либо людей, предметов, значит, они входят в их число.
Большинство театров относятся к числу федеральных объектов. | Она относится к разряду деловых, самодостаточных женщин.
5. Когда вы каким-либо образом относитесь к человеку, значит, вы испытываете к нему такие чувства или таким образом о нём думаете.
Муж относится к ней очень бережно. | Мой отчим всегда очень хорошо к нам относился.
6. Когда вы каким-либо образом относитесь к чему-либо, например к какому-либо делу, виду деятельности, вы таким образом думаете о нём и обращаетесь с ним, исходя из своих внутренних убеждений, принципов.
Каждый человек должен внимательно относиться к своему здоровью. | Он очень добросовестно относится к порученному делу. | Я неплохо отношусь к современному авангарду в искусстве.
1. несовер. к отнестись. «Я часто позволял себе относиться об этом человеке непочтительно и свысока.» Достоевский.
3. Иметь связь с чем-нибудь, касательство к чему-нибудь, принадлежать к чему-нибудь (книжн.). Это к делу не относится. Рисунок относится к следующей главе. «У меня есть одно письмо, до вас относящееся.» Достоевский.
4. Давать при делении на другое количество определенное частное (всегда в сравнении с другой парой количеств; мат.). «А» относится к «В», как «х» к «у».
2. Иметь касательство к кому-чему-н. Вопрос относится непосредственно к теме. Это к делу не относится.
3. Входить в число кого-чего-н., в какой-н. разряд, множество. О. к числу оптимистов.
1. к Отнести́ и Отнести́сь.
2. Иметь отношение к кому-, чему-л., касаться кого-, чего-л.; быть обращённым к кому-л. Вопрос относится непосредственно к данной теме. Это к делу не относится. Читал всё, что относилось к кооперации. Все замечания относились к новичкам. Слова напутствия относятся к новобранцам.
3. Находиться в каком-л. соответствии, соотношении с чем-л. Образ в поэзии точно так же относится к действительному образу, как слово относится к действительному предмету.
4. Входить в состав, в разряд, в число кого-, чего-л. Мой коллега относится к людям доброжелательным и любезным. Кит относится к классу млекопитающих. Художник относится к группе авангардистов. О. к семейству романских языков.
2. Входить в состав, в разряд, в число кого-, чего-л.
Относиться к классу млекопитающих. Относиться к людям какого-л. склада.
3. к кому-чему и (устар.) до кого-чего. Иметь отношение (в 3 знач.) к кому-, чему-л., касаться кого-, чего-л.
По возвращении моем напечатал я стихотворение, не относившееся ко взятию Арзрума. Пушкин, Путешествие в Арзрум (ранняя редакция).
— Как мне не знать-с всего, что до вашего семейства относится? Тургенев, Дворянское гнездо.
В Петрозаводске я засел в архивах и библиотеке и начал читать все, что относилось к Петровскому заводу. Паустовский, Золотая роза.
Быть обращенным к кому-л., предназначенным для кого-л.
Молодая девушка, к которой относилось это восклицание, остановилась. Тургенев, Накануне.
4. Находиться в каком-л. соответствии, соотношении с чем-л.
(иметь отношение к кому-, чему-л.; касаться чего-л.) к кому-чему и (устар.) до кого-чего. В Петрозаводске я засел в архивах и библиотеке и начал читать все, что относилось к Петровскому заводу (Паустовский). Как мне не знать-с всего, что до вашего семейства относится? (Тургенев).
1. относи́ться, отношу́сь, отно́симся, отно́сишься, отно́ситесь, отно́сится, отно́сятся, относя́сь, относи́лся, относи́лась, относи́лось, относи́лись, относи́сь, относи́тесь, относи́вшийся, относи́вшаяся, относи́вшееся, относи́вшиеся, относи́вшегося, относи́вшейся, относи́вшегося, относи́вшихся, относи́вшемуся, относи́вшейся, относи́вшемуся, относи́вшимся, относи́вшийся, относи́вшуюся, относи́вшееся, относи́вшиеся, относи́вшегося, относи́вшуюся, относи́вшееся, относи́вшихся, относи́вшимся, относи́вшейся, относи́вшеюся, относи́вшимся, относи́вшимися, относи́вшемся, относи́вшейся, относи́вшемся, относи́вшихся
2. относи́ться, отношу́сь, отно́симся, отно́сишься, отно́ситесь, отно́сится, отно́сятся, относя́сь, относи́лся, относи́лась, относи́лось, относи́лись, относи́сь, относи́тесь, относя́щийся, относя́щаяся, относя́щееся, относя́щиеся, относя́щегося, относя́щейся, относя́щегося, относя́щихся, относя́щемуся, относя́щейся, относя́щемуся, относя́щимся, относя́щийся, относя́щуюся, относя́щееся, относя́щиеся, относя́щегося, относя́щуюся, относя́щееся, относя́щихся, относя́щимся, относя́щейся, относя́щеюся, относя́щимся, относя́щимися, относя́щемся, относя́щейся, относя́щемся, относя́щихся, относи́вшийся, относи́вшаяся, относи́вшееся, относи́вшиеся, относи́вшегося, относи́вшейся, относи́вшегося, относи́вшихся, относи́вшемуся, относи́вшейся, относи́вшемуся, относи́вшимся, относи́вшийся, относи́вшуюся, относи́вшееся, относи́вшиеся, относи́вшегося, относи́вшуюся, относи́вшееся, относи́вшихся, относи́вшимся, относи́вшейся, относи́вшеюся, относи́вшимся, относи́вшимися, относи́вшемся, относи́вшейся, относи́вшемся, относи́вшихся
1. иметь отношение (или касательство), касаться кого, чего
2. проявлять какое отношение, встречать кого, что, принимать кого, что, смотреть на кого, на что, глядеть на кого, на что
Относительно – это что означает?
Выражение «относительно» крайне популярно в разговорной речи. Им пользуются абсолютно все без каких-либо исключений. Так говорят подростки, пренебрежительно сплевывая или напуская на себя равнодушный вид. Им пользуются аспиранты, студенты, телеведущие и бизнесмены – произносят это слово они обычно с выражением превосходства или же некоей загадочности на лице, когда пытаются потянуть время и обдумать то, что нужно сказать. Используют его в своей речи и другие люди. Между тем, объяснить, в чем смысл этого выражения, могут далеко не все.
Что означает это слово?
Если оно используется как наречие, то его смысл в следующем:
То есть, «относительно» – это неопределенно, до каких-либо нечетких пределов.
В том случае, если слово используется в качестве предлога, его смысловое значение таково:
В значении предлога в современной разговорной речи слово практически не используется.
Примеры употребления в речи
В том случае, если слово является наречием, предложения с ним звучат следующим образом:
При употреблении его в качестве предлога высказывания могут быть такими:
В значении предлога слово часто встречается на страницах литературных произведений русских классиков, например, Чехова или Тургенева.
Что означает это слово в философии?
Существует устойчивое выражение «все относительно». Как понять его смысл? Для этого придется обратиться к философии, ведь именно оттуда оно и пришло в повседневную речь.
Вообще в этой науке используется термин «относительность». Смысл данного понятия в рассмотрении предмета во взаимосвязи с чем-либо. Это означает, что данным термином называют отношение, установленное между рассматриваемым предметом и его опосредованной сутью, содержанием. Эта взаимосвязь и является непосредственной сущностью этого понятия.
Соответственно, фразу «все относительно» можно понять в двух значениях:
Что именно подразумевается в данный момент, проясняет общий контекст.
Таким образом, на вопрос о том, что такое «относительно», можно ответить просто – «неопределенно». Именно в таком значении слово используется в разговорах наиболее часто.
Смысл
Если заглянем в словарь, то найдем там только два значения:
Стоит сказать, что в первом значении – это наречие, а во втором – это предлог, употребляемый в книжной речи.
Можно легко представить такой диалог:
— Василий Щукин – это хороший футболист?
— Смотря с кем сравнивать. До Месси ему пока далеко, но он молод. У него все впереди.
— Вы пытаетесь мне сказать, что он силен относительно, это так надо понимать?
— Именно. И думаю, такими талантами, как Вася, не разбрасываются.
Иллюстрация ко второму значению следует далее.
Тут тоже диалог удобнее всего. Например, подчиненный пришел к шефу узнать о задаче, которую они обговаривали накануне.
Сотрудник несмело приоткрывает дверь в кабинет руководителя:
— Иван Николаевич, вы один?
— Да, Александр Дмитриевич, проходите, не стесняйтесь.
— Шеф, я пришел узнать относительно того дела, той операции, о которой мы говорили вчера.
— Вы еще скажите: «Операции “Ы”!»
— Чтобы никто не догадался! – усмехнулся начальник.
Синонимы
Альтернатив у слова, как смыслов, немного. Воспользуемся теми определениями, что уже были, и добавим некоторые другие. Вот они:
Почему оценка «относительно» так популярна сегодня
— Какая у тебя зарплата, большая?
Конечно, читатель скажет, что можно не обращать на это внимания, жить своей жизнью и не воспринимать информационный шум и эти бесконечные цифры. Читатель как всегда прав. Но так случилось, что взрослые люди существуют в мире статистики, поэтому заслониться от нее не так уж и просто.
В любом случае мы узнали ответ на вопрос, что значит слово «относительно».
Соотношения
Соотношением называют некоторую взаимосвязь между сущностями нашего мира. Это могут быть числа, физические величины, предметы, продукты, явления, действия и даже люди.
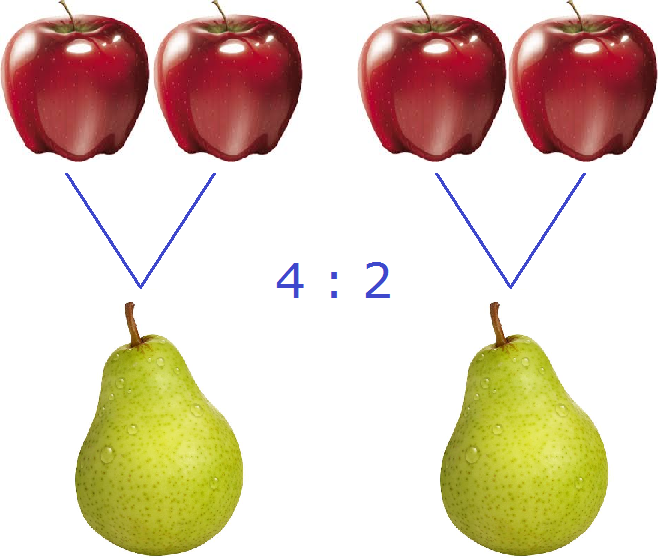
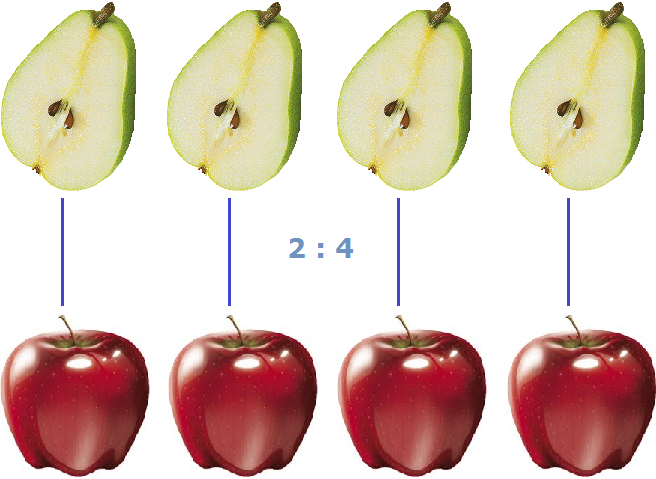
В повседневной жизни, когда речь заходит о соотношениях, мы говорим «соотношения того-то и того-то». Например, если в вазе лежит 4 яблока и 2 груши, то мы говорим «соотношения яблок и груш» или если поменять местами яблоки и груши, то «соотношения груш и яблок».
В математике соотношение чаще употребляется как «отношение того-то к тому-то». Например, соотношение четырёх яблок и двух груш, которые мы рассматривали выше, в математике будет читаться как «отношение четырех яблок к двум грушам» или если поменять местами яблоки и груши, то «отношение двух груш к четырем яблокам».
Запишем соотношение четырех яблок и двух груш с помощью символа соотношения:
Это соотношение можно прочитать как «четыре к двум» либо «соотношение четырех яблок и двух груш» либо «четыре яблока относится к двум грушам»
В дальнейшем соотношение мы будем называть просто отношением.
Что такое отношение?
Отношением в математике называют частное двух чисел.
Данное отношение представляет собой деление числа 4 на число 2. Если выполнить это деление, мы получим ответ на вопрос сколько яблок приходится на единицу груши
Получили 2. Значит четыре яблока и две груши (4 : 2) соотносятся (взаимосвязаны друг с другом) так, что на одну грушу приходится два яблока
На рисунке показано, как четыре яблока и две груши соотносятся между собой. Видно, что на каждую грушу приходятся два яблока.
Чтобы найти значение дроби нужно вспомнить, как делить меньшее число на большее
Получили 0,5. Переведём эту десятичную дробь в обыкновенную:
Сократим полученную обыкновенную дробь на 5
Получили ответ 
(половину груши). Значит две груши и четыре яблока (2 : 4) соотносятся (взаимосвязаны друг с другом) так, что на одно яблоко приходится половина груши
На рисунке показано, как две груши и четыре яблока соотносятся между собой. Видно, что на каждое яблоко приходится половинка груши.
Числа, из которых составлено отношение, называют членами отношения. Например, в отношении 4 : 2 членами являются числа 4 и 2.
Рассмотрим другие примеры соотношений. Для приготовления чего-либо составляется рецепт. Рецепт строят из соотношений между продуктами. Например, для приготовления овсяной каши обычно требуется стакан хлопьев на два стакана молока или воды. Получается соотношение 1 : 2 («один к двум» или «один стакан хлопьев на два стакана молока»).
Если перевернуть соотношение 1 : 2 то получится соотношение 2 : 1 («два к одному» или «два стакана молока на один стакан хлопьев»). Преобразуем соотношение 2 : 1 в дробь, получим 
. Вычислив эту дробь, получим 2. Значит два стакана молока и один стакан хлопьев соотносятся (взаимосвязаны друг с другом) так, что на один стакан хлопьев приходятся два стакана молока.
Пример 2. В классе 15 школьников. Из них 5 – это мальчики, 10 – девочки. Можно записать соотношение девочек и мальчиков 10 : 5 и преобразовать это соотношение в дробь 
. Вычислив эту дробь получим 2. То есть девочки и мальчики соотносятся между собой так, что на каждого мальчика приходятся две девочки
На рисунке показано, как десять девочек и пять мальчиков соотносятся между собой. Видно, что на каждого мальчика приходятся две девочки.
Соотношение не всегда можно обращать в дробь и находить частное. В некоторых случаях это будет нелогично.
Так, если перевернуть отношение получится 
, а это уже отношение мальчиков к девочкам. Если вычислить эту дробь получается 0,5. Получается, что пять мальчиков относятся к десяти девочкам так, что на каждую девочку приходится половина мальчика. Математически это конечно верно, но с точки зрения реальности не совсем разумно, ибо мальчик это живой человек и его нельзя просто так взять и разделить, как грушу или яблоко.
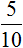
Умение построить правильное отношение — важный навык при решении задач. Так в физике, отношение пройденного расстояния ко времени есть скорость движения.
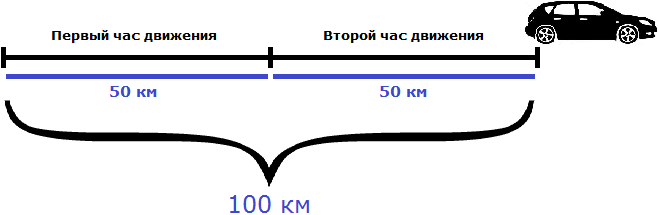
Предположим, что автомобиль проехал 100 километров за 2 часа. Тогда отношение пройденных ста километров к двум часам будет скоростью движения автомобиля:
Скоростью принято называть расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. А отношение, как было сказано ранее, позволяет узнать сколько количества одной сущности приходится на единицу другой. В нашем примере отношение ста километров к двум часам показывает сколько километров приходится на один час движения. Видим, что на каждый час движения приходятся 50 километров
Пример 2. Отношение стоимости товара к его количеству есть цена одной единицы товара
Если мы взяли в магазине 5 шоколадных батончиков и их общая стоимость составила 100 рублей, то мы можем определить цену одного батончика. Для этого нужно найти отношение ста рублей к количеству батончиков. Тогда получим, что на один батончик приходятся 20 рублей
Сравнение величин
Ранее мы узнали, что отношение между величинами разной природы образуют новую величину. Так, отношение пройденного расстояния ко времени есть скорость движения. Отношение стоимости товара к его количеству есть цена одной единицы товара.
Но отношение можно использовать и для сравнения величин. Результат выполнения такого отношения есть число, показывающее во сколько раз первая величина больше второй или какую часть первая величина составляет от второй.
Чтобы узнать во сколько раз первая величина больше второй, в числитель отношения нужно записать большую величину, а в знаменатель меньшую величину.
Чтобы узнать какую часть первая величина составляет от второй, в числитель отношения нужно записать меньшую величину, а в знаменатель большую величину.
Рассмотрим числа 20 и 2. Давайте узнаем во сколько раз число 20 больше числа 2. Для этого находим отношение числа 20 к числу 2. В числителе отношения записываем число 20, а в знаменателе — число 2
Значение данного отношения равно десяти
Отношение числа 20 к числу 2 есть число 10. Это число показывает во сколько раз число 20 больше числа 2. Значит число 20 больше числа 2 в десять раз.
Пример 2. В классе 15 школьников. 5 из них это мальчики, 10 – девочки. Определить во сколько раз девочек больше мальчиков.
Записываем отношение девочек к мальчикам. В числителе отношения записываем количество девочек, в знаменатель отношения — количество мальчиков:
Значение данного отношения равно 2. Значит в классе из 15 человек девочек в два раза больше мальчиков.
Здесь уже не стоит вопрос о том, сколько девочек приходятся на одного мальчика. В данном случае отношение используется для сравнения количества девочек с количеством мальчиков.
Пример 3. Какую часть число 2 составляет от числа 20.
Находим отношение числа 2 к числу 20. В числителе отношения записываем число 2, а в знаменателе — число 20
Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее
Значение отношения числа 2 к числу 20 есть число 0,1
В данном случае десятичную дробь 0,1 можно перевести в обыкновенную. Такой ответ будет проще для восприятия:
Значит число 2 от числа 20 составляет одну десятую часть.
Можно сделать проверку. Для этого найдём от числа 20. Если мы всё сделали правильно, то должны получить число 2
Получили число 2. Значит одна десятая часть от числа 20 есть число 2. Отсюда делаем вывод, что задача решена верно.
Пример 4. В классе 15 человек. 5 из них это мальчики, 10 – девочки. Определить какую часть от общего количества школьников составляют мальчики.
Записываем отношение мальчиков к общему количеству школьников. В числителе отношения записываем пять мальчиков, в знаменателе — общее количество школьников. Общее количество школьников это 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения записываем число 15
Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае число 5 нужно разделить на число 15
При делении 5 на 15 получается периодическая дробь. Переведём эту дробь в обыкновенную
Сократим полученную дробь на 3
Получили окончательный ответ 
. Значит мальчики составляют одну треть от всего класса
На рисунке видно, что в классе из 15 школьников треть класса составляют 5 мальчиков.
Если для проверки найти от 15 школьников, то мы получим 5 мальчиков
Записываем отношение числа 35 к числу 5. В числитель отношения нужно записать число 35, в знаменатель — число 5, но не наоборот
Значение данного отношения равно 7. Значит число 35 в семь раз больше числа 5.
Пример 6. В классе 15 человек. 5 из них это мальчики, 10 – девочки. Определить какую часть от общего количества составляют девочки.
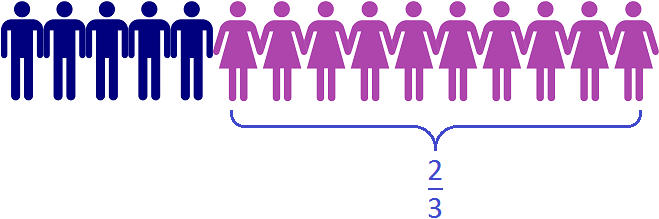
Записываем отношение девочек к общему количеству школьников. В числителе отношения записываем десять девочек, в знаменателе — общее количество школьников. Общее количество школьников это 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения записываем число 15
Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае, число 10 нужно разделить на число 15
При делении 10 на 15 получается периодическая дробь. Переведём эту дробь в обыкновенную
Сократим полученную дробь на 3
На рисунке видно, что в классе из 15 школьников две трети класса составляют 10 девочек.
Если для проверки найти от 15 школьников, то получим 10 девочек
Пример 7. Какую часть 10 см составляют от 25 см
Записываем отношение десяти сантиметров к двадцати пяти сантиметрам. В числителе отношения записываем 10 см, в знаменателе — 25 см
Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае число 10 нужно разделить на число 25
Переведём полученную десятичную дробь в обыкновенную
Сократим полученную дробь на 2
Получили окончательный ответ 
. Значит 10 см составляют от 25 см.
Пример 8. Во сколько раз 25 см больше 10 см
Записываем отношение двадцати пяти сантиметров к десяти сантиметрам. В числителе отношения записываем 25 см, в знаменателе — 10 см
Найдём значение данного отношения
Получили ответ 2,5. Значит 25 см больше 10 см в 2,5 раза (в два с половиной раза)
Важное замечание. При нахождении отношения одноименных физических величин эти величины обязательно должны быть выражены в одной единице измерения, в противном случае ответ будет неверным.
Например, если мы имеем дело с двумя длинами и хотим узнать во сколько раз первая длина больше второй или какую часть первая длина составляет от второй, то обе длины сначала нужно выразить в одной единице измерения.
Пример 9. Во сколько раз 150 см больше 1 метра?
Сначала сделаем так, чтобы обе длины были выражены в одной единице измерения. Для этого переведем 1 метр в сантиметры. Один метр это сто сантиметров
1 м = 100 см
Теперь находим отношение ста пятидесяти сантиметров к ста сантиметрам. В числителе отношения записываем 150 сантиметров, в знаменателе — 100 сантиметров
Найдём значение данного отношения
Получили ответ 1,5. Значит 150 см больше 100 см в 1,5 раза (в полтора раза).
А если бы не стали переводить метры в сантиметры и сразу попытались найти отношение 150 см к одному метру, то у нас получилось бы следующее:
Получилось бы, что 150 см больше одного метра в сто пятьдесят раз, а это неверно. Поэтому обязательно нужно обращать внимание на единицы измерения физических величин, которые участвуют в отношении. Если эти величины выражены в разных единицах измерения, то для нахождения отношения этих величин, нужно перейти к одной единице измерения.
Пример 10. В прошлом месяце зарплата человека составляла 25000 рублей, а в текущем месяце зарплата выросла до 27000 рублей. Определить во сколько раз выросла зарплата
Записываем отношение двадцати семи тысяч к двадцати пяти тысячам. В числителе отношения записываем 27000, в знаменателе — 25000
Найдём значение данного отношения
Получили ответ 1,08. Значит зарплата выросла в 1,08 раза. В будущем, когда мы познакомимся с процентами, такие показатели как зарплата будем выражать в процентах.
Пример 11. Ширина многоквартирного дома 80 метров, а высота 16 метров. Во сколько раз ширина дома больше его высоты?
Записываем отношение ширины дома к его высоте:
Значение данного отношения равно 5. Значит ширина дома в пять раз больше его высоты.
Свойство отношения
Отношение не изменится если его члены умножить или разделить на одно и тоже число.
Это одно из важнейших свойств отношения следует из свойства частного. Мы знаем, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится. А поскольку отношение является ничем иным как делением, то свойство частного работает и для него.
В нашем примере удобнее разделить члены отношения на их наибольший общий делитель (НОД).
НОД членов 10 и 5 это число 5. Поэтому можно разделить члены отношения на число 5
Получили новое отношение . Это есть отношение два к одному (2:1). Данное отношение, как и прошлое отношение 10:5 показывает, что на одного мальчика приходятся две девочки.
На рисунке показано отношение 2 : 1 (два к одному). Как и в прошлом отношении 10 : 5 на одного мальчика приходятся две девочки. Другими словами, отношение не изменилось.
Пример 2. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз в первом классе девочек больше мальчиков? Во сколько раз во втором классе девочек больше мальчиков?
В обоих классах девочек в два раза больше мальчиков, поскольку отношения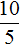 
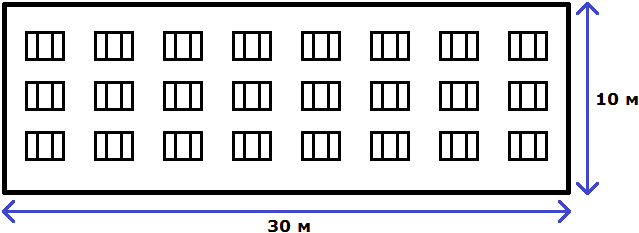
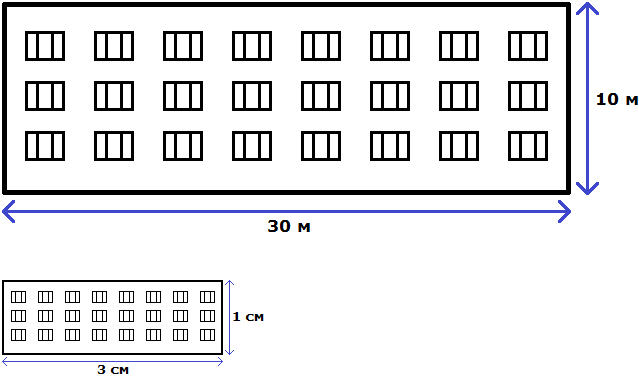
и 
равны одному и тому же числу.
Свойство отношения позволяет строить различные модели, которые имеют схожие параметры с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 метров и высоту 10 метров.
Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров
3 м = 300 см
1 м = 100 см
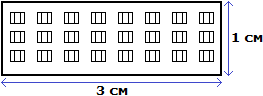
Имеем отношение 300 см : 100 см. Разделим члены этого отношения на 100. Получим отношение 3 см : 1 см. Теперь можно нарисовать дом с шириной 3 см и высотой 1 см
Конечно нарисованный дом намного меньше реального дома, но неизменным осталось отношение ширины и высоты. Это позволило нам нарисовать дом, максимально похожий на реальный
Отношение можно понимать и другим образом. Изначально было сказано, что у реального дома ширина составляет 30 метров, а высота 10 метров. Итого получается 30+10, то есть 40 метров.
Эти 40 метров можно понимать, как 40 частей. Отношение 30 : 10 говорит о том, что 30 частей приходится на ширину, а 10 частей на высоту.
Далее члены отношения 30 : 10 были разделены на 10. В результате получилось отношение 3 : 1. Это отношение можно понимать, как 4 части, три из которых приходится на ширину, одна — на высоту. В этом случае обычно требуется узнать сколько конкретно метров приходится на ширину и высоту.
Другими словами, нужно узнать сколько метров приходится на 3 части и сколько метров приходится на 1 часть. Сначала надо узнать сколько метров приходится на одну часть. Для этого общие 40 метров нужно разделить на 4, поскольку в отношении 3 : 1 всего четыре части
Далее с помощью умножения определяют сколько метров приходятся на ширину и высоту. Члены, которые даны в отношении используют в качестве сомножителя.
Определим сколько метров приходится на ширину:
Определим сколько метров приходится на высоту:
Несколько членов отношения
Если в отношении дано несколько членов, то их можно понимать как части от чего-либо.
Отношение 2 : 1 : 3 говорит о том, что мама получила 2 части, папа — 1 часть, дочка — 3 части. Другими словами, каждый член отношения 2 : 1 : 3 это определенная часть от 18 яблок:
Узнаем сколько яблок приходится на одну часть. Для этого 18 яблок разделим на 6
18 : 6 = 3 (яблока на одну часть)
Узнаем сколько яблок получила мама:
Узнаем сколько яблок получил папа:
Узнаем сколько яблок получила дочка:
4 килограмма нового серебра будет содержать 3 части никеля, 4 части цинка и 13 частей меди. Сначала узнаем сколько всего частей будет в четырех килограммах серебра:
3 + 4 + 13 = 20 (частей)
Определим сколько килограммов будет приходиться на одну часть:
Определим сколько килограммов никеля будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что три части сплава содержат никель. Поэтому умножаем 0,2 на 3:
0,2 кг × 3 = 0,6 кг никеля
Теперь определим сколько килограммов цинка будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что четыре части сплава содержат цинк. Поэтому умножаем 0,2 на 4:
0,2 кг × 4 = 0,8 кг цинка
Теперь определим сколько килограммов меди будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что тринадцать частей сплава содержат медь. Поэтому умножаем 0,2 на 13:
0,2 кг × 13 = 2,6 кг меди
Значит, чтобы получить 4 кг нового серебра, нужно взять 0,6 кг никеля, 0,8 кг цинка и 2,6 кг меди.
Определим сколько граммов сплава приходится на одну часть. В условии сказано, что для изготовления куска латуни требуется 120 г меди. Также сказано, что три части сплава содержат медь. Если разделить 120 на 3, мы узнаем сколько граммов сплава приходится на одну часть:
120 : 3 = 40 граммов на одну часть
Теперь определим сколько требуется цинка для изготовления куска латуни. Для этого 40 граммов умножим на 2, поскольку в отношении 3 : 2 указано, что две части содержат цинк:
40 г × 2 = 80 граммов цинка
Пример 4. Взяли два сплава золота и серебра. В одном количество этих металлов находится в отношении 1 : 9, а в другом 2 : 3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золото и серебро относилось бы как 1 : 4?
Решение
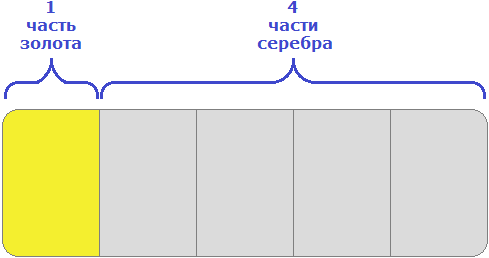
15 кг нового сплава должны состоять в отношении 1 : 4. Это отношение говорит о том, что на одну часть сплава будет приходиться золото, а на четыре части будет приходиться серебро. Всего же частей пять. Схематически это можно представить следующим образом
Определим массу одной части. Для этого сначала сложим все части (1 и 4), затем массу сплава разделим на количество этих частей
1 + 4 = 5
15 кг : 5 = 3 кг
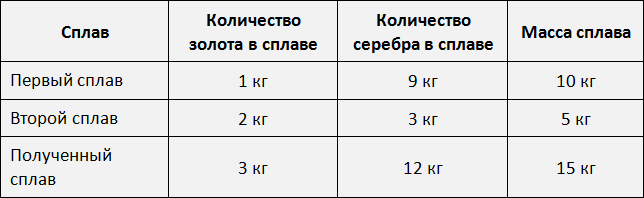
Одна часть сплава будет иметь массу 3 кг. Тогда в 15 кг нового сплава будет содержáться 3 × 1 = 3 кг золота и серебра 3 × 4 = 12 кг серебра.
Поэтому для получения сплава массой 15 кг нам нужно 3 кг золота и 12 кг серебра.
Теперь ответим на вопрос задачи — « Сколько нужно взять каждого сплава? »
Первого сплава мы возьмем 10 кг, поскольку золото и серебро в нём находятся в отношении 1 : 9. То есть этот первый сплав даст нам 1 кг золота и 9 кг серебра.
Второго сплава мы возьмем 5 кг, поскольку золото и серебро находятся в нём в отношении 2 : 3. То есть этот второй сплав даст нам 2 кг золота и 3 кг серебра.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже