Что значит отношение эквивалентности
1.4.3. Отношения эквивалентности
Определение. Бинарное отношение, являющееся одновременно рефлексивным, симметричным и транзитивным, называется Отношением эквивалентности.
Если R является отношением эквивалентности, то часто вместо ARb пишут A
b, если ясно, о каком отношении эквивалентности R идет речь.
Примеры Отношений эквивалентности.
1. Отношения подобия треугольников.
2. Отношение тождества на множестве алгебраических выражений.
3. Отношение параллельности на множестве прямых.
4. Отношение учиться в одной группе на множестве студентов.
5. Отношение получить одну и ту же оценку по математике на экзамене.
6. Отношение иметь одинаковый остаток при делении на 7 на множестве
7. На множестве комплексных чисел С отношение иметь одинаковый модуль: z1
Контрпримеры (отношения, не являющиеся отношениями эквивалентности).
1. 
2. 
3. Отношение 
Определение. Пусть на множестве А задано отношение эквивалентности
и A

Свойства классов смежности.
1. 
a, ввиду рефлективности).
Доказательство. Проверим, что [A] 

b, то по свойству транзитивности X
b И, следовательно, X
a. Далее, поменяв местами A и B и все повторив, получим [B]
Замечание. Свойство 2 означает, что любой класс смежности однозначно определяется любым своим представителем. Тем самым, все представители класса равноправны при определении этого класса.
3. Любые два класса эквивалентности либо не пересекаются, либо совпадают.
Доказательство. Пусть C 



[C] 
Определение. Совокупность всех различных смежных классов множества А по отношению эквивалентности
Замечание. Свойство 3 показывает, что такая совокупность всех различных смежных классов (фактор—множество) представляет собой некоторое разбиение множества А.
Обратно, всякое разбиение множества А=А1




Действительно, если задано разбиение множества A (такое, как выше), то положим A
b, если a и B принадлежат одному и тому же подмножеству Ai (рефлексивность и симметричность очевидны, транзитивность легко следует из того, что Ai

1.11 Отношение эквивалентности
Отношение эквивалентности представляет собой строгое математическое определение таких обыденных понятий как «одинаковость» или «неразличимость».
Y. Отношение эквивалентности А в множестве М означает, что упорядоченная пара (X, Y) принадлежит множеству А Ì М´М.
Отношение эквивалентности обладает свойствами:
· Симметричности: если X
· Транзитивности: если X
Важнейшее значение эквивалентности состоит в том, что это отношение определяет признак, который допускает разбиение множества М на непересекающиеся подмножества, называемые КласСами эквивалентности. И наоборот: всякое разбиение множества М на непересекающиеся подмножества определяет между элементами этого множества некоторое отношение эквивалентности.
Например: Отношение «проживать в одном доме», заданное в множестве жителей города, является эквивалентностью и разбивает это множество на непересекающиеся подмножества людей, являющихся соседями по дому.
Все элементы, принадлежащие некоторому классу МI разбиения <М1, М2. МN> множества М на классы эквивалентности, связаны отношением эквивалентности. Любой из этих элементов определяет данный класс и может служить его Представителем или Эталоном.
Произвольное отношение эквивалентности определяет на некотором множестве обобщенную форму равенства. Классы эквивалентности состоят из всех тех элементов, которые неразличимы с точки зрения данного отношения эквивалентности. При этом каждый класс определяется его представителем (эталоном) и отождествляется с некоторым общим свойством или совокупностью свойств входящих в него элементов.
Предельным случаем отношения эквивалентности является Тождественное равенство. Очевидно, что единственный элемент, тождественно равный какому-либо данному элементу, есть этот самый элемент. Следовательно, в данном случае имеем самое полное разбиение, при котором классы эквивалентности содержат только по одному элементу исходного множества.
Рассмотрим матрицу отношения эквивалентности.
Элементы, принадлежащие некоторому классу эквивалентности, попарно эквивалентны между собой, а их сечения совпадают. Следовательно, столбцы матрицы отношения эквивалентности для элементов одного класса одинаковы и содержат «1» во всех строках, которые соответствуют этим элементам. Так как классы эквивалентности не пересекаются, то в столбцах различных классов не будет единиц в одинаковых строках. Если расположить элементы множества так, чтобы в каждом классе эквивалентности принадлежащие ему элементы стояли рядом, то единичные элементы матрицы образуют непересекающиеся квадраты, диагонали которых располагаются на главной диагонали матрицы.
Например: Пусть множество М разбито на классы эквивалентности следующим образом:
Признаки, по которым элементы множества разбиваются на классы, могут быть самыми разнообразными, но все же такой признак не вполне произволен.
СОДЕРЖАНИЕ
Обозначение
Определение
Примеры
Простой пример
Отношения эквивалентности
Все следующие отношения являются отношениями эквивалентности:
Отношения, не являющиеся эквивалентами
Связь с другими отношениями
Корректная определенность при отношении эквивалентности
Класс эквивалентности, фактормножество, разбиение
Класс эквивалентности
Набор частных
Проекция
Ядро эквивалентности
Раздел
Подсчет разделов
Основная теорема об отношениях эквивалентности
Ключевой результат связывает отношения эквивалентности и разбиения:
В обоих случаях клетки разбиения X являются классами эквивалентности X по
, каждый элемент X принадлежит уникальному классу эквивалентности X по
Сравнение отношений эквивалентности
лучше, чем ≈, если каждый класс эквивалентности
является подмножеством класса эквивалентности ≈, и, таким образом, каждый класс эквивалентности ≈ является объединением классов эквивалентности
тоньше, чем ≈, если раздел, созданный с помощью
, является уточнением раздела, созданного с помощью ≈.
Отношение эквивалентности равенства является наилучшим отношением эквивалентности на любом множестве, в то время как универсальное отношение, связывающее все пары элементов, является самым грубым.
Создание отношений эквивалентности
Алгебраическая структура
Теория групп
Таким образом, для данного отношения эквивалентности
Соответствующее мышление можно найти у Розена (2008: глава 10).
Категории и группоиды
Преимущества рассмотрения отношения эквивалентности как частного случая группоида включают:
Решетки
Отношения эквивалентности и математическая логика
Из теории моделей следует, что свойства, определяющие отношение, могут быть доказаны независимыми друг от друга (и, следовательно, необходимыми частями определения) тогда и только тогда, когда для каждого свойства могут быть найдены примеры отношений, не удовлетворяющих данному свойству, но удовлетворяющих все остальные свойства. Следовательно, три определяющих свойства отношений эквивалентности могут быть доказаны взаимно независимыми на следующих трех примерах:
Свойства, определяемые в логике первого порядка, которыми отношение эквивалентности может обладать или не обладать, включают:
Евклидовы отношения
Евклида «S Элементы включает в себя следующее„Общее понятие 1“:
Вещи, которые равны одному и тому же, также равны друг другу.
( aRc ∧ bRc ) → aRb (лево-евклидово соотношение) ( cRa ∧ cRb ) → aRb (Правое евклидово соотношение)
Следующая теорема связывает евклидовы отношения и отношения эквивалентности:
Отношение эквивалентности



Бинарное отношение называется эквивалентностью, если оно рефлексивно, симметрично и транзитивно. Эквивалентность обозначается символом
на множестве А по элементу а называется множество, определенное следующим образом:
Разумеется, элемент а, для которого класс эквивалентности определен таким образом, также входит в этот класс в силу рефлексивности отношения эквивалентности.
Множество классов эквивалентности связано с разбиением несущего множества. Вообще разбиением множества М называется множество, элементами которого являются множества подмножества М; объединение этих подмножеств равно М, а пересечения попарно пусты. Пустое множество не входит в разбиение.
Можно доказать, что отношение эквивалентности “
” на А образует разбиение А/
множества А, причем элементами разбиения являются классы эквивалентности. Разбиение называется минимальным, если в каждый класс эквивалентности входит по одному элементу. Примером такого отношения является отношение х
у Û х=у, х,у Î А. Разбиение называется максимальным, если оно образует единственный класс эквивалентности, в который входят все элементы А.
Множество классов эквивалентности элементов множества А по эквивалентности “
” называется фактор-множеством А по “
Примерами отношений эквивалентности являются отношения равенства чисел (образует максимальное разбиение), конгруэнтности треугольников (классы эквивалентности включают все конгруэнтные треугольники), равенства множеств, равномощности множеств, сравнимости чисел по модулю m (это отношение определяет множества чисел, дающих одинаковый остаток при делении на m).
Теорема. Если “
” – отношение эквивалентности, заданное на произвольном непустом множестве А, то существует разбиение R
=
y тогда и только тогда, когда х и у принадлежат к одному и тому же классу разбиения.
— эквивалентность на А и A/
=
. Докажем существование разбиения R
, равного фактор множеству A/
· Пусть aÎA – произвольный элемент А. Обозначим Аа = a> – класс эквивалентности по элементу а. Тогда аÎАа, и, следовательно · Докажем теперь, что попарные пересечения классов эквивалентности пусты. Пусть a,b Î A, aÎ Aa, b Î Ab, Aa и Ab –два класса эквивалентности. Пусть Аa Ç Ab ¹Æ. Тогда существует хотя бы один элемент сÎА такой, что с Î Аa и с Î Аb, т.е. с b. Пусть z – произвольный элемент множества Аа. Тогда z с. По свойству транзитивности отношения эквивалентности получаем z b, следовательно, по свойству транзитивности z b. Следовательно, z Î Ab. Следовательно, Aa Í Ab. Обратное включение доказывается аналогично. Следовательно, пересечение Aa и Ab не пусто тогда и только тогда, когда это одно и то же множество. Таким образом, доказано, что множество классов эквивалентности образуют разбиение множества А. ¨ Таблица 2 Свойства отношения эквивалентности Определение. Отношение R на множестве Х называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно. Пример. Рассмотрим отношение «х однокурсник у» на множестве студентов педфака. Оно обладает свойствами: 1) рефлексивности, т.к. каждый студент является однокурсником самому себе; 2) симметричности, т.к. если студент х является однокурсником студента у, то и студент у является однокурсником студента х; Таким образом, данное отношение обладает свойствами рефлексивности, симметричности и транзитивности, а значит, является отношением эквивалентности. При этом множество студентов педфака можно разбить на подмножества, состоящие из студентов, обучающихся на одном курсе. Получаем 5 подмножеств. Теорема. Если на множестве Х задано отношение эквивалентности, то оно разбивает это множество на попарно непересекающиеся подмножества (классы эквивалентности). Верно и обратное утверждение: если какое-либо отношение, заданное на множестве Х, порождает разбиение этого множества на классы, то оно является отношением эквивалентности. Пример. На множестве Х = <1; 2; 3; 4; 5; 6; 7; 8>задано отношение «иметь один и тот же остаток при делении на 3». Является ли оно отношением эквивалентности? Данное отношение обладает свойствами рефлексивности, симметричности и транзитивности, следовательно, является отношение эквивалентности и разбивает множество Х на классыэквивалентности. В каждом классе эквивалентности будут числа, которые при делении на 3 дают один и тот же остаток: Х1 = <3; 6>, Х2 = <1; 4; 7>, Х3 = <2; 5; 8>. Считают, что класс эквивалентности определяется любым своим представителем, т.е. произвольным элементом этого класса. Так, класс равных дробей можно задать, указав любую дробь, принадлежащую этому классу. 2.3. Функции, уравнения, неравенства 2.3.1. Понятие функции. Способы задания функций. Прямая и обратная пропорциональности. Функцией называется такое соответствие между числовым множеством x и множеством R действительных чисел, при котором каждому числу из множества x сопостовляется единственное число из множества R. (тетрадь) Функцией наз-ся такая зависимость переменной у от переменной х, при которой каждому значению х соответсвует единственное значение у. Способы задания функций: 1) Формула. Нарпимер: у=кх+в, где к, в – числа Прямой пропорциональностью называют функцию, которая может быть задана с помощью формулы у=кх, где к ≠ 0, называемое коэффициентом пропорциональности. 2.3.2. Понятие числового выражения и выражения с переменной. Числовые равенства, неравенства и их свойства. Записи, 3+7, 424:8, 3*2-4, (25+3)*2-17 называются числовыми выражениями. Они конструируются из чисел, знаков действий и скобок. Считают, что каждое число также является числовым выражением. В записи 2а+3 такая буква а называется переменной, а сама запись 2а+3 – выражением с переменной. Переменную можно обозн-ть любой буквой латинского алфавита. Таким образом, переменная – это знак (Символ), кот-ый разрешается заменять числами. Пусть а и b – два числовых выражения. Соединим их знаком равенства. Получим предложение а=b, кот-ое наз-ют числовым равенством. Числовое рав-во истинно, если значения числовых выражений, стоящих в левой и правой частях рав-ва, совпадают. Свойства истинных числовых рав-в: 1) Если к обеим частям истинного числового рав-ва а=b умножить на одно и то же числовое выражение с, имеющее смысл, то получим также истинное числовое рав-во a+c=b+c 2) Если обе части истинного числового рав-ва a=b умножить на одно и то же числовое выражение с, имеющее смысл, то получим также истинное числовое рав-во ac=bc. Пусть а и b – два числовых выражения. Соединим их знаком «>» (или b (или a b прибавить одно и тоже числовое выражение с, имеющее смысл, то получим также истинное числовое нерав-во a+c>b+c. 2) Если обе части истинного числового неравенства a>b умножить на одно и то же числовое выражение с, имеющее смысл и принимающее полож-ое значение, то получим также истинное числовое нерав-во ac>bc. 3) Если обе части истинного числового неравенства a>b умн-ть на одно и то же числовое выражение с, имеющее смыл и примающее отриц-ое значение, то, чтобы получить истинное числовое нерав-во, необходимо знак нерав-ва поменять на противоп-ый, т.е. получить нерав-во ac b Теорема 2: Ɐ а, в, с € N 3) а>с и в>с, то справ-во либо 1) или 2) Правила выч-я числа из суммы: Чтобы вычислить число из суммы достаточно вычесть это число из одного из слаг-х и к получ-му рез-ту прибавить другое слагаемое. Теорема 3: Ɐ а,в,с € N если а>в+с, то а-(в=с)=(а-в)-с=(а-с)-в. Правила вычисления из числа суммы чисел: Чтобы вычесть из числа суммы чисел дост-но вычесть из этого числа послед-но каждое слагаемое одно за другим. Делением нат. чисел наз-ся операция, удовл-я условию: а:в=с ↔ а=в*с Теорема 1: Для того чтобы сущ-ло частное двух нат-х чисел а и в, необ-мо, чтобы в в (а-в):с → а:с-в:с → Для того чтобы разделить разность на число, дост-но разделить на это число уменьшаемое и вычитание и из первого частного вычесть второе. 3.2. Теоретико-множественный смысл натурального числа, нуля и операций над Количественное натуральное число а получается в результате счета элементов конечного множества А: а = n(А). Это же число а может быть получено и при пересчете элементов другого множества, например, В. Но если а = п(В), то множества А и В равномощны, поскольку содержат поровну элементов. Каждому классу соответсвует одно и только одно натуральное число, каждому нат-му числу – один и только один класс равномощных конечных мн-в. Каждому конечному мн-ву А соотв-ет одно и только нат-ое число а=n(А), но каждому нат-му числу а соотв-ют различные равномощные мн-ва одного класса эквивалентности. Так как каждый класс равномощных конечных множеств однозначно определяется выбором какого-нибудь его представителя, то о натуральном числе «три» можно сказать, что это общее свойство класса множеств, равномощных, например, множеству сторон треугольника, а о натуральном числе «четыре», что это общее свойство класса множеств, равномощных, например, множеству вершин квадрата. Число «нуль» с теоретико-множественных позиций рассматривается как число элементов пустого множества: 0 = п(0). Итак, натуральное число а как характеристику количества можно рассматривать с двух позиций: 1) как число элементов в множестве А, получаемое при счете, т.е. 2) как общее свойство класса конечных равномощных множеств. 3.2.1. Теоретико-множественный смысл суммы двух целых неотрицательных чисел. Законы сложения. Суммой целых неотриц-ых чисел a и b наз-ют число элементов в обьединении неперескающихся множеств А и В, таких, что n (А)=а, n (В)=b. Т.е. а+в= n (A) + n (В) = n (АUВ). А пересекается В = пустое мн-во. Законы сложения: переместительный и сочетательный. 2. Сочеательный закон (ассоциативность): Для любых целых неотриц-ых чисел а, b, c вып-ся рав-во (а+ b )+ c = a + ( b + c ) Дата добавления: 2019-07-15 ; просмотров: 1897 ; Мы поможем в написании вашей работы!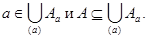
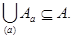
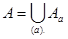
ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ И ПОРЯДКА. РАЗБИЕНИЕ МНОЖЕСТВА НА КЛАССЫ ЭКВИВАЛЕНТНОСТИ.
а = п(А), причем А




