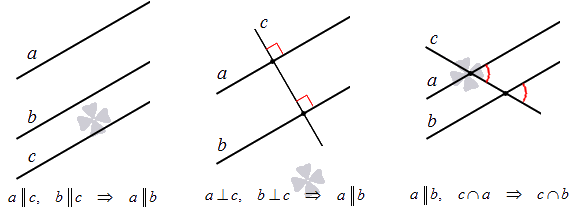Что значит отличная прямая
Прямая линия. Понятие прямой, ее свойства.
Наглядно прямую линию может продемонстрировать туго натянутый шнур, кромка стола, край листа бумаги, место, соединения двух стен комнаты, луч света. При начертании прямых линий на практике применяют линейку.
Прямой линии присущи такие характерные особенности:
1.У прямой линии нет ни начала ни конца, то есть она бесконечна. Существует возможность начертить только ее часть.
2.Через две произвольные точки можно провести прямую линию, и притом только одну.
3. Через произвольную точку можно провести не ограниченное количество прямых на плоскости.
4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны.
Для обозначения прямой линии используют или одну малую букву латинского алфавита, или две большие буквы, написанные в двух различных местах этой прямой.
Если на прямой линии указать точку, то в результате получим два луча:
Лучом называют часть прямой линии, ограниченную с одной стороны. Для обозначения луча применяют или одну малую букву латинского алфавита, или две большие буквы, из которых одна обозначается в начале луча.
Часть прямой, ограниченная с обеих сторон, именуют ее отрезком. Отрезок, как и прямая линия, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.
Линию, сформированную несколькими отрезками, не лежащими на одной прямой, принято называть ломаной. Когда концы ломаной совпадают, то такая ломаная именуется замкнутой.
Геометрия 7 класс.
Точка, прямая и отрезок
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.
Точка — элементарная фигура, не имеющая частей.
Прямая состоит из множества точек и простирается бесконечно в обе стороны.
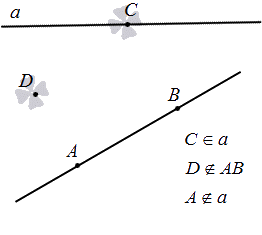
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
Как обозначить прямую
Прямую обычно обозначают одной маленькой латинской буквой.
Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.
Задача № 1 из учебника Атанасян 7-9 класс
Решение задачи
Опишем взаимное расположение точек и прямой.
Как обозначается пересечение прямых
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).
Прямые e и f не имеют общей точки — т.е. они не пересекаются.
Взаимное расположение прямой и точек
Через одну точку (·)A можно провести сколько угодно прямых.
Через две точки (·)A и (·)B можно провести только одну прямую.
Сколько общих точек имеют две прямые
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.
Второй случай расположения прямых
Третий случай расположения прямых
Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Задача № 3 из учебника Атанасян 7-9 класс
Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Решение задачи
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.
Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или три.
Что такое отрезок
Отрезок — часть прямой, ограниченная двумя точками.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.
Прямая линия
Прямая линия — это линия, не имеющая неровностей, скруглений и углов. Прямая линия бесконечна, она не имеет ни начала, ни конца. В геометрии прямая линия называется просто прямой.
Для изображения прямой на бумаге используется линейка. Чтобы начертить прямую, надо провести черту вдоль края линейки:
Так как прямая бесконечна, то какой бы длины не была проведена черта, она будет изображать только часть прямой.
Обозначение прямой
Прямая обозначается одной маленькой латинской буквой, например прямая a, или двумя большими латинскими буквами, поставленными при любых двух точках, лежащих на этой прямой, например прямая AB:
Обратите внимание, что точки на прямой можно обозначать короткими чёрточками.
Свойства прямой
1. Через любые две точки можно провести только одну прямую линию.
Это основное свойство прямой. Оно часто используется на практике, для прокладывания прямых линий с помощью двух каких-либо объектов.
2. Если две любые точки прямой лежат на плоскости, то все точки этой прямой лежат на той же плоскости.
3. Через одну точку можно провести бесконечно много прямых.
4. Есть точки лежащие на прямой и не лежащие на ней.
Точки N и M лежат на прямой a. Точка L не лежит на прямой a.
5. Из трёх разных точек, лежащих на одной прямой, только одна может лежать между двумя другими точками.
На рисунке изображена прямая с тремя точками A, B и C, лежащими на ней. Про эти точки можно сказать:
точка B лежит между точками A и C, точка B разделяет точки A и C
Также можно сказать:
точки B и C лежат по одну сторону от точки A, они не разделяются точкой A
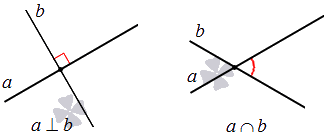
6. Две прямые, лежащие на одной плоскости, или пересекаются друг с другом в одной точке, или являются параллельными.
Прямая на плоскости – необходимые сведения
Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.
Прямая на плоскости – понятие
Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.
Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.
Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.
Взаимное расположение прямой и точки
На каждой прямой и в каждой плоскости могут быть отмечены точки.
Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.
Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.
Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:
Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.
Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.
Точка делит прямую на две части, называемые лучами. Имеем аксиому:
Взаимное расположение прямых на плоскости
Расположение прямых на плоскости может принимать вид двух состояний.
Две прямые на плоскости могут совпадать.
Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.
Две прямые на плоскости могут пересекаться.
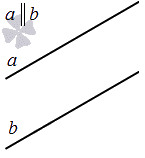
Две прямые на плоскости могут быть параллельны.
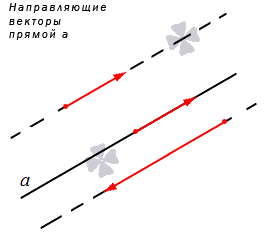
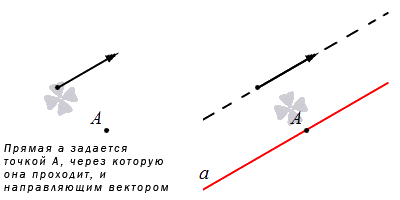
Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.
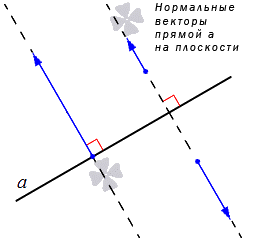
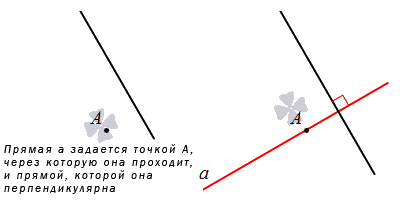
Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.
Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.
Для этого приводим необходимы факторы, доказывающие их взаимное расположение:
Рассмотрим это на рисунках.
Способы задания прямой на плоскости
Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.
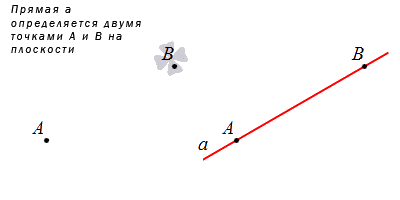
Прямая задается при помощи указанных двух точек, расположенных в плоскости.
Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.
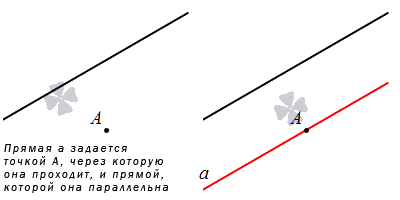
Прямая может быть задана через точку и прямую, которой она параллельна.
Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.
Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.
Прямая задается через указанную точку и направляющий вектор.
Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.
Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:
Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.
И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.
отличный от
Смотреть что такое «отличный от» в других словарях:
отличный — Блестящий, блистательный, божественный, великолепный, волшебный, восхитительный, дивный, обворожительный, обольстительный, образцовый, отменный, очаровательный, пленительный, превосходный, прекрасный, прелестный, удивительный, чудный. Отлично, на … Словарь синонимов
Отличный — Отличный: «Отличный» эскадренный миноносец проекта 30 К. «Отличный» эскадренный миноносец проекта 956 … Википедия
ОТЛИЧНЫЙ — ОТЛИЧНЫЙ, отличная, отличное; отличен, отлична, отлично. 1. Различающийся, отличающийся от кого чего нибудь (книжн. устар.). Совершенно отличные характеры. Отличное от прежнего решение. 2. Очень хороший, превосходный, выдающийся. Отличный… … Толковый словарь Ушакова
ОТЛИЧНЫЙ — ОТЛИЧНЫЙ, ая, ое; чен, чна. 1. от кого (чего). Отличающийся, иной. Отличное от прежнего решение. 2. Очень хороший, превосходный. Отличная игра актёров. Продукция отличного качества. Отлично (нареч.) отдохнул. 3. отлично, частица. Выражение… … Толковый словарь Ожегова
отличный от — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN other than … Справочник технического переводчика
отличный — 1 • в корне отличный • принципиально отличный 2 • отличный аппетит … Словарь русской идиоматики
отличный — прил., употр. часто Морфология: отличен, отлична, отлично, отличны; отличнее; нар. отлично 1. Когда один предмет, явление и т. п. отличны от других, они на них непохожи, имеют другие признаки, особенности. Американский исторический опыт во многом … Толковый словарь Дмитриева
Отличный — I прил. Отличающийся от кого либо или от чего либо; иной. II прил. Очень хороший, превосходный, выдающийся. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Отличный — I прил. Отличающийся от кого либо или от чего либо; иной. II прил. Очень хороший, превосходный, выдающийся. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
отличный — отличный, отличная, отличное, отличные, отличного, отличной, отличного, отличных, отличному, отличной, отличному, отличным, отличный, отличную, отличное, отличные, отличного, отличную, отличное, отличных, отличным, отличной, отличною, отличным,… … Формы слов