Что значит основное свойство дроби
Основное свойство дроби: формулировка, доказательство, примеры применения
В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.
Основное свойство дроби, формулировка, доказательство и примеры
Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:
Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.
a · m b · m = a b и a : m b : m = a b
Разберем пример, который графически проиллюстрирует основное свойство дроби.
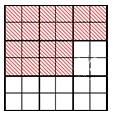
Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4 · 9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4 · 5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:
Чтобы закрепить теорию, разберем решение примера.
Решение
Ответ: да, полученная в итоге дробь будет равна исходной.
Применение основного свойства дроби
Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.
Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.
Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.
Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.
Основное свойство дроби
Все обыкновенные дроби обладают следующим свойством:
Если числитель и знаменатель обыкновенной дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.
Это свойство называется основным свойством дроби. С его помощью можно получать новые дроби, равные данной дроби.
В общем виде основное свойство дроби можно выразить так:
где a — нуль или натуральное число, b и m — натуральные числа.
Согласно данному свойству, одну и ту же часть единицы можно выразить с помощью дробей в разных формах.
Пример. Рассмотрим три круга, у которых жёлтым цветом закрашена некоторая одинаковая часть:
У первого круга закрашено 


Все три дроби равны между собой 
Можно заметить, что члены второй дроби в 2 раза больше числителя и знаменателя первой дроби, а члены третьей — в 3 раза.
Умножив оба члена дроби 

Умножив оба члена дроби 

Или наоборот, разделив числитель и знаменатель дроби 

Разделив члены дроби 

Умножение числителя и знаменателя дроби на одно и то же число называют расширением дроби. Деление числителя и знаменателя на одно и то же число называют сокращением дроби.
Основное свойство дроби обычно применяется при сокращении дробей и при приведении дробей к общему знаменателю.
ОБЫКНОВЕННАЯ ДРОБЬ
Ключевые слова конспекта: дроби, обыкновенная дробь, правильные и неправильные дроби, основное свойство дроби, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части.
Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.
Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.
Правильная и неправильная дробь
Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.
Основное свойство дроби
Определение. Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.
Основное свойство дроби используют при сокращении дробей. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дробей.
Сравнение дробей
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Арифметические действия с обыкновенными дробями
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.
При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.
Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!
Общий случай сложения (вычитания) дробей.
Умножение дробей
Деление дробей
Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.
При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.
Нахождение части от целого (дроби от числа)
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.
Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.
Нахождение целого по его части (числа по его дроби)
Чтобы найти целое по его части, нужно число, соответствующее этой части, разделить на числитель дроби, выражающей эту часть, и результат умножить на знаменатель той же дроби.
Задача нахождения целого по его части по существу является задачей нахождения числа по его дроби. Чтобы найти число по его дроби, необходимо данное значение разделить на эту дробь.
Это конспект по теме «Обыкновенная дробь». Выберите дальнейшие действия:
Основное свойство дроби
Основное свойство дроби – что это за свойство? В чем заключается смысл этого свойства?
Для того чтобы разобраться в данном вопросе, будем использовать разные пособия, например, геометрические фигуры, вырезанные из бумаги.
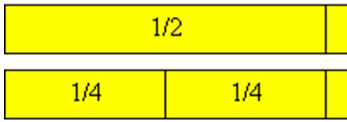
Возьмем две ОДИНАКОВЫЕ (это очень важно!) полоски.
Первую полоску разделим пополам.
У нас получились 2 одинаковые части. Каждая часть — это 1 доля (см. статью здесь) от целого отрезка или 1/2. В целом прямоугольнике 2 вторых доли.
Теперь каждую половинку разделим еще пополам.
У нас получились 4 одинаковые части. Каждая часть составляет тоже одну долю от прямоугольника, но это уже – 1/4. В целом прямоугольнике четыре четвертых доли. А в половине две четвертых доли.
Сравним доли: вторую и четвертую.
1/2 > 1/4.
Вставьте число вместо «окошка», чтобы равенство стало верным: 1/2 = □ /4? (1/2 = 2/4).
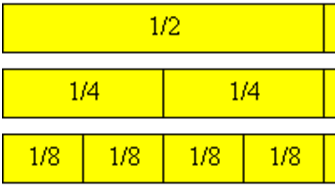
Теперь четвертые части разделим еще пополам.
У нас получилось 8 одинаковых частей, одна из которых это – 1/8. В прямоугольнике восемь восьмых.
Итак: 1/2 = 2/4 = 4/8.
Давайте подумаем: что изменяется и почему?
Рассмотрим дроби попарно.
1/2 и 2/4. Посмотрим на числители: 1 и 2. Как они изменились? Числитель во второй дроби стал больше: 1 – 2, т.е. 1 х 2 = 2.
Что же происходит со знаменателем? Так же: было 2, стало 4: 2 х 2 = 4.
Вторая пара 2/4 и 4/8. Посмотрим на числитель: было 2, стало 4: 2 х 2 = 8.
А знаменатель? Было 4, стало 8, т.е. 4 х 2 = 8.
Получается: когда числитель и знаменатель в дроби умножить на 2, то получатся равные дроби.
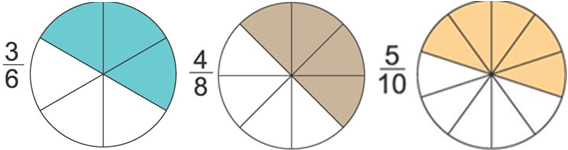
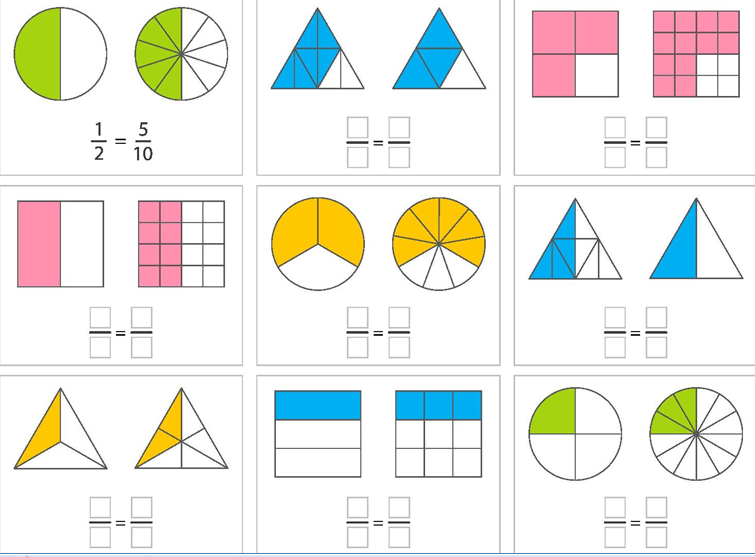
Пример 2: Круги разделили на части. Первый круг — на 6 равных частей и закрасили 3 части, т.е. 3/6. Второй — на 8 равных частей и закрасили 4, т.е. 4/8. Третий разделили на 10 частей и закрасили 5, т.е. 5/10.
Если внимательно посмотреть на эти части, то видно, раскрашены одинаковые части — половина — 1/2.
То есть: 1/2 = 3/6 = 4/8 = 5/10.
Давайте подумаем: как изменяются дроби?
Первая пара: 1/2 = 3/6 —
сравним числители: 1 – 3. Что произошло? Числитель увеличился. Был 1 – стал 3, т.е. 1 х 3 = 3.
Что же происходит со знаменателем? Так же: был 2 – стал 6: 2 х 3 = 6.
Получается: когда числитель и знаменатель в дроби умножить на 3, то получатся равные дроби.
Вторая пара: 1/2= 4/8 –
сравним числители: 1 – 4. Что произошло? Числитель увеличился. Был 1 – стал 4, т.е. 1 х 4 = 4.
Что же происходит со знаменателем? То же самое: был 2 – стал 8 — 2 х 4 = 8.
Получается: когда числитель и знаменатель в дроби умножить на 4, то получатся равные дроби.
Третья пара: 1/2= 5/10 –
сравним числители: 1 – 5. Что произошло? Числитель увеличился. Был 1 – стал 5, т.е. 1 х 5 = 5.
А знаменатель? То же самое: был 2 – стал 10: 2 х 5 = 10.
Получается: когда числитель и знаменатель в дроби умножить на 5, то получатся равные дроби.
Вывод: дробь УВЕЛИЧИВАЕТСЯ – если и числитель, и знаменатель умножают на одно и то же число.
А можно уменьшить дробь?
Разобраться в этом нам поможет схема.
Начертим отрезок, разделим его на 12 равных частей и возьмем 8 частей.
Точно такой же отрезок разделим на 3 одинаковых части и возьмем 2 части.
Мы видим, новые отрезки одинаковые по длине, значит и дроби 8/12 и 2/3 равны.
Посмотрим на числитель: 8 и 2. Как из 8 получить 2? Надо 8 : 4 = 2.
Знаменатель: был 12, стал 4. Как из 12 сделать 4? Надо разделить на 4.
Это свойство будем использовать, если надо дроби привести к другому знаменателю, а также при сокращении дробей.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 76
Обыкновенные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доля целого
Доля — это каждая равная часть, из суммы которых состоит целый предмет.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:
Понятие дроби
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
Виды дробей:
Какие еще бывают дроби:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.
Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Полученные числа запишем справа сверху над числителем.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо: