Что значит описать множество точек
Урок алгебры в 7-м классе по теме «Множества точек на координатной плоскости»
Разделы: Математика
I. Оргмомент
II. Актуализация знаний
1. Определить координаты точек.
2. Построить отрезок LE, если L(–1; 2), Е(4; 5).
Построить прямую РТ, если Р(0; 3), Т(–1; –2)
III. Постановка проблемы
Приготовить пять координатных плоскостей.
Отметьте указанные точки на координатных плоскостях
1) А(3; 1), В(4; –1), С(–5; –2).
2) М(3; –2), N(–4; –2), К(1.5; –2)
5) Q(0; 3), N(0; 5), L(0; –1/2)
Посмотрите на чертежи, что можно сказать о расположении точек:
В первом случае?
В остальных случаях?
Что общего?
Мы выяснили, что общее в 2–4 рисунках то, что точки лежат на одной прямой.
IV. «Открытие» детьми нового знания
Подумайте, как можно записать множество точек, изображенных на рисунке
Какое условие является общим для этих точек?
А как это условие записать на языке алгебры? у = 3
(ордината равна 3)
На рис.2 проведите через отмеченные точки у = – 2
прямую, запишите множество этих точек.
Проведите на остальных рисунках через отмеченные точки прямые.
А как бы вы записали на языке алгебры множества точек, изображенных на рисунке 3? 4? 5?
Подумайте, а затем проверим правильность записей.
Что означают эти записи на математическом языке?
Множество точек расположенных где? На координатной плоскости
Итак, тема нашего урока:
А цель урока?
Учитель еще раз формулирует тему и цель урока, записывает тему на доске.
Изобразите на координатной плоскости множество точек, удовлетворяющих условию:
У обучающихся На доске
х = 5
х = – 4
у = – 4
у = 1
Проверяем правильность построения и записи.
А теперь давайте попробуем изобразить множество точек, удовлетворяющих условию х > 3.
Как можно это условие прочитать на русском языке? – точки, большие 3
Чтобы построить точку в координатной плоскости, необходимо, что знать?
Прочитайте условие х > 3
Построим в координатной плоскости прямую х = 3
Где будут располагаться точки, абсцисса которых больше 3?
Покажите несколько таких точек
А множество всех точек удовлетворяющих условию х > 3 можно показать с помощью штриховки
х > 3 задает полуплоскость, расположенную правее прямой х = 3 и все точки этой прямой.
Изобразите множество точек, удовлетворяющих условию у 1.
Проверяем правильность построения.
Постройте множество точек у > 1.
Каким свойством обладают точки этого множества у них ордината больше 1
А как они должны располагаться относительно – выше
прямой у = 1
А точки прямой у = 1 удовлетворяют условию y > 1 нет
А как это показать? – не знаем
В этом случае прямая у = 1 изображается пунктиром.
Изобразим множество точек, удовлетворяющих условию у > 1.
Приглашается ученик к доске.
Изобразите множество точек, удовлетворяющих условию:
Выделите множество точек, удовлетворяющих одновременно всем этим условиям.
Какую фигуру получили?
VI. Самостоятельная работа с последующей самопроверкой
1. Опишите на алгебраическом языке множества точек, изображенные на рисунках.
1. 
2. Изобразите на координатной плоскости множества точек, удовлетворяющих условию:
Множество точек. Изображение некоторых множеств точек на плоскости.
В первом случае прямые параллельны оси ординат, во втором – абсцисс.
На координатной прямой неравенству х 3. Проанализируем, что это за точки:
— множество точек, абсцисса которых больше или равна 3
— точки, лежащие правее прямой х = 3 и на прямой.
Алгоритм построения будет иметь вид:
— строим в координатной плоскости прямую: х = 3;
— определяем, где будут находиться точки, абсцисса которых больше 3; ответ – правее;
— множество всех точек удовлетворяющих условию х > 3 покажем при помощи штриховки;
х > 3 задает полуплоскость, находящаяся правее прямой х = 3 и все точки этой прямой. Прямую изображаем одной цельной линией, этим указываем, что все точки расположенные на прямой так же включены во множество.
Представим множество точек, удовлетворяющих условию у 1.
Следовательно, они будут находиться выше прямой у = 1. В соответствии со знаком неравенства точки прямой у = 1 не удовлетворяют условию y > 1. Графически мы это покажем, изобразив прямую у = 1 пунктиром.
Представим множество точек, соответствующих условию у > 1 так:
Описание множества точек прямоугольника
На координатной плоскости постройте прямоугольник с вершинами в точках A (-1; 3), B (-1; 6), C (5; 3), D (5; 6). Опишите множество точек этого прямоугольника.
Ребята, проверьте, пожалуйста, не уверена в решении.
Формализованное описание выбора количества из множества по определенному свойству элементов
Доброго времени суток! Необходимо математически описать, что N равно количество сотрудников.
Доказать, что множества точек шаров равномощны
Здравствуйте! Не получается с задачей: Доказать, что множества точек шаров радиусов 5 и 7.
Дать геометрическое описание множества точек комплексной плоскости, удовлетворяющих указанным условиям
Дать геометрическое описание множества точек комплексной плоскости, удовлетворяющих указанным.
Вы имеете в виду так: X ∈ [-1, 5]? И тогда множество точек прямоугольника будет по-прежнему X x Y?
Да, так правильно. Эквивалентные описания:
Найти координаты двух угловых точек прямоугольника не симметричного осям координат
Даны координаты двух нижних угловых точек прямоугольника повернутого на угол alpha (А(x;y) B(x;y)).
Множества предельных точек
Даны множества X и Y X’ и Y’ это множесва их предельных точек соответсвенно. Выполняется ли (X V.
Уравнение множества точек
Кто-нибудь помогите студенту-заочнику решить задачку: Нужно составить уравнение множества точек.
Уравнение множества точек
Условие: Составить уравнение множества точек, сумма расстояний которых от точек A (1;0) и B (0;1).
Составить уравнение множества точек
Составить уравнение множества точек, для каждой из которых выполняется условие, сумма квадратов.
Составить уравнение множества точек.
Собственно в чём суть: Необходимо составить уравнение множества точек, для каждой из которых.
Общее уравнение плоскости : описание, примеры, решение задач
В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
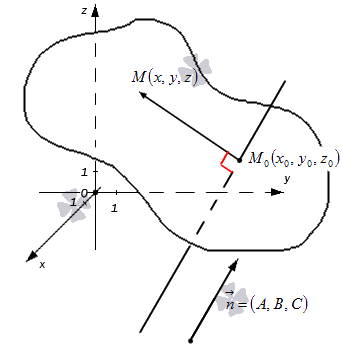
Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.
Раскроем чуть шире смысл теорем.
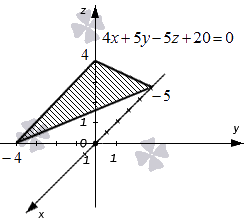
Укажем пример как иллюстрацию этих утверждений.
Общее уравнение плоскости, проходящей через точку
Решение
Подставим координаты точки М 0 в исходной уравнение плоскости:
Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.
Решение
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Возможно получить это уравнение другим способом.
Решение
Рассмотрим два способа решения.
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
Неполное общее уравнение плоскости
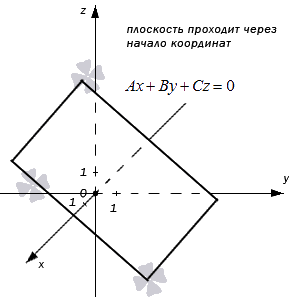
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0
Решение
Задачу возможно решить еще одним способом.
Решение
Обозначение, запись и изображение числовых множеств
Из большого количества разнообразных множеств особо интересными и важными являются числовые множества, т.е. те множества, элементами которых служат числа. Очевидно, что для работы с числовыми множествами необходимо иметь навык записи их, а также изображения их на координатной прямой.
Запись числовых множеств
N – множество всех натуральных чисел; Z – множество целых чисел; Q – множество рациональных чисел; J – множество иррациональных чисел; R – множество действительных чисел; C – множество комплексных чисел.
Напомним также следующие обозначения:
Рассмотрим теперь схему описания числовых множеств на примере основных стандартных случаев, наиболее часто используемых на практике.
Таким же образом, объединяя различные числовые промежутки и множества отдельных чисел, возможно дать описание любому числовому множеству, состоящему из действительных чисел. На основе сказанного становится понятно, для чего вводятся различные виды числовых промежутков, такие как интервал, полуинтервал, отрезок, открытый числовой луч и числовой луч. Все эти виды промежутков совместно с обозначениями множеств отдельных чисел дают возможность через их объединение описать любое числовое множество.
Изображение числовых множеств на координатной прямой
В практических примерах удобно использовать геометрическое толкование числовых множеств – их изображение на координатной прямой. К примеру, такой способ поможет при решении неравенств, в которых нужно учесть ОДЗ – когда нужно отобразить числовые множества, чтобы определить их объединение и/или пересечение.
Зачастую и не указывают начало отсчета и единичный отрезок:
В большинстве случаев возможно не соблюдать абсолютную точность чертежа: вполне достаточно схематичного изображения без соблюдения масштаба, но с сохранением взаимного расположения точек относительно друг друга, т.е. любая точка с бОльшей координатой должна быть правее точки с меньшей. С учётом сказанного уже имеющийся чертеж может выглядеть так:
Отдельно из возможных числовых множеств выделяют числовые промежутки интервалы, полуинтервалы, лучи и пр.)
Информация, приведенная в данной статье, призвана помочь получить навык видеть запись и изображение числовых множеств так же легко, как и отдельных числовых промежутков. В идеале записанное числовое множество сразу должно представляться в виде геометрического образа на координатной прямой. И наоборот: по изображению должно с легкостью формироваться соответствующее числовое множество через объединение числовых промежутков и множеств, являющихся отдельными числами.