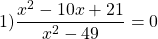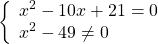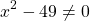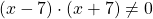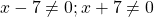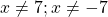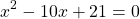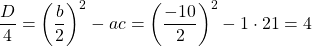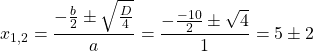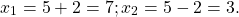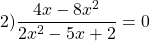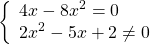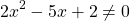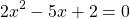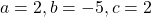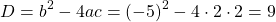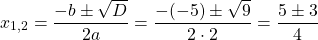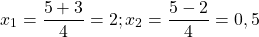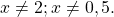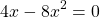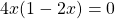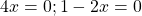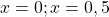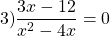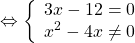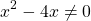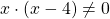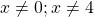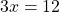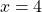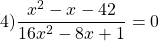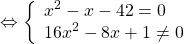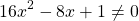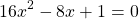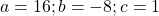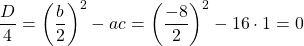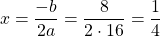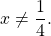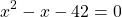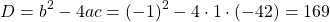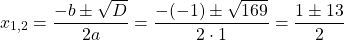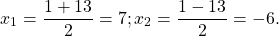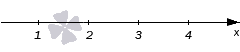Что значит нули числителя
Метод интервалов
Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.
1. Рассмотрим, например, такое неравенство
Метод интервалов позволяет решить его за пару минут.
В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.
Метод интервалов основан на следующем свойстве дробно-рациональной функции.
Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).
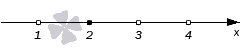
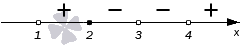
Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.
Эти точки разбивают ось на промежутков.
При левая часть неравенства отрицательна.
Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.
Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:
Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.
Ты нашел то, что искал? Поделись с друзьями!
2. Рассмотрим еще одно неравенство.
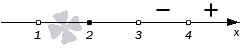
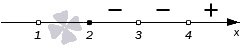
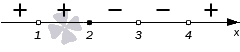
При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак :
При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак :
Наконец, при 3′ alt=’x>3′ /> все множители положительны, и левая часть имеет знак :
Почему нарушилось чередование знаков? Потому что при переходе через точку «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:
Левая часть та же, что и в предыдущей задаче. Та же будет и картина знаков:
В задаче на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:
— которое легко решается методом интервалов.
5. Рассмотрим еще одно неравенство, на вид совсем простое:
Мы поступим по другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:
Дробь равна нулю
Когда дробь равна нулю?
Дробная черта — это знак деления. При делении нуля на любое число, кроме нуля, получим нуль. На нуль делить нельзя.
Таким образом, дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля.
Решение многих задач в алгебре сводится к решению дробно рациональных уравнений, которые, в свою очередь, сводятся к уравнению типа «дробь равна нулю».
Схематически решение уравнения типа «дробь равна нулю» можно изобразить так:
Таким образом, чтобы решить уравнение типа «дробь равна нулю», надо:
1) Найти значения переменной, при которых знаменатель обращается в нуль.
2) Приравнять к нулю числитель и решить получившееся уравнение.
3) Проверить, нет ли среди корней уравнения «числитель равен нулю» значений, при которых знаменатель обращается в нуль. Если есть, их следует исключить.
Дробь равна нулю, если числитель равен нулю, а знаменатель — отличен от нуля, поэтому это уравнение равносильно системе
Находим значения переменной, при которых знаменатель обращается в нуль:
Можно приравнять выражение, стоящее в левой части неравенства, к нулю, и решать как обычное неполное квадратное уравнение. Можно решать как уравнение, только вместо знака равенства каждый раз писать «≠».
При этих значениях переменной выражение, стоящее в левой части уравнения, не имеет смысла (так как на нуль делить нельзя).
Решаем уравнение, в котором числитель равен нулю.
Так как D/4>0, уравнение имеет два корня:
Первый из корней — посторонний (он не удовлетворяет условию x≠7), поэтому в ответ записывает только корень 3. Ответ: 3.
Это уравнение равносильно системе
Его корни — значения переменной, при котором выражение, стоящее в левой части уравнения, не имеет смысла.
Общий множитель 4x выносим за скобки
Второй корень не подходит (он не удовлетворяет условию x≠0,5).
Переходим к решению уравнения 3x-12=0. Это — линейное уравнение. Неизвестное — в одну сторону, известное — в другую с противоположным знаком:
Полученный корень является посторонним, так как не удовлетворяет условию x≠4. Значит, исходное уравнение типа «дробь равна 0» корней не имеет.
Решаем квадратное уравнение
Так как D/4=0, квадратное уравнение имеет один корень
Теперь решаем уравнение
Посторонних корней нет (оба корня удовлетворяют условию x≠1/4).
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Метод интервалов, примеры, решения.
Метод интервалов (или как его еще иногда называют метод промежутков) – это универсальный метод решения неравенств. Он подходит для решения разнообразных неравенств, однако наиболее удобен в решении рациональных неравенств с одной переменной. Поэтому в школьном курсе алгебры метод интервалов вплотную привязывают именно к рациональным неравенствам, а решению других неравенств с его помощью практически не уделяют внимания.
В этой статье мы детально разберем метод интервалов и затронем все тонкости решения неравенств с одной переменной с его помощью. Начнем с того, что приведем алгоритм решения неравенств методом интервалов. Дальше поясним, на каких теоретических аспектах он базируется, и разберем шаги алгоритма, в частности, подробно остановимся на определении знаков на интервалах. После этого перейдем к практике и покажем решения нескольких типовых примеров. А в заключение рассмотрим метод интервалов в общем виде (то есть, без привязки к рациональным неравенствам), другими словами, обобщенный метод интервалов.
Навигация по странице.
Алгоритм
Чтобы сделать дальнейший разговор предметным, сразу запишем алгоритм решения неравенств указанного выше вида методом интервалов, а потом разберемся, что да как да почему. Итак, по методу интервалов:
На чем базируется метод?
Так мы плавно подошли к вопросу определения знаков на промежутках, но не будем перескакивать через первый шаг метода интервалов, подразумевающий нахождение нулей числителя и знаменателя.
Как находить нули числителя и знаменателя?
С нахождением нулей числителя и знаменателя дроби указанного в первом пункте вида обычно не возникает никаких проблем. Для этого выражения из числителя и знаменателя приравниваются к нулю, и решаются полученные уравнения. Принцип решения уравнений такого вида подробно изложен в статье решение уравнений методом разложения на множители. Здесь лишь ограничимся примером.
Для нахождения нулей числителя и знаменателя в общем случае, когда в левой части неравенства дробь, но не обязательно рациональная, также числитель и знаменатель приравниваются к нулю, и решаются соответствующие уравнения.
Как определять знаки на интервалах?
Самый надежный способ определения знака выражения из левой части неравенства на каждом промежутке состоит в вычислении значения этого выражения в какой-либо одной точке из каждого промежутка. При этом искомый знак на промежутке совпадает со знаком значения выражения в любой точке этого промежутка. Поясним это на примере.
Существует и другой подход к определению знаков, состоящий в нахождении знака на одном из интервалов и его сохранении или изменении при переходе к соседнему интервалу через нуль. Нужно придерживаться следующего правила. При переходе через нуль числителя, но не знаменателя, или через нуль знаменателя, но не числителя, знак изменяется, если степень выражения, дающего этот нуль, нечетная, и не изменяется, если четная. А при переходе через точку, являющуюся одновременно и нулем числителя, и нулем знаменателя, знак изменяется, если сумма степеней выражений, дающих этот нуль, нечетная, и не изменяется, если четная.
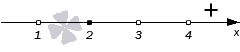
Кстати, если выражение в правой части неравенства имеет вид, указанный в начале первого пункта этой статьи, то на крайнем правом промежутке будет знак плюс.
Чтобы все стало понятно, рассмотрим пример.
А дальше наступает момент определения знаков на промежутках. Как мы заметили перед этим примером, на крайнем правом промежутке (4, +∞) будет знак +:
Понятно, что применение рассмотренного метода особенно оправдано, когда вычисление значения выражения связано с большим объемом работы. К примеру, вычислите-ка значение выражения 

Будем считать, что с нахождением знаков на промежутках разобрались.
Примеры решения неравенств методом интервалов
Теперь можно собрать воедино всю представленную информацию, достаточную для решения неравенств методом интервалов, и разобрать решения нескольких примеров.
Метод интервалов, примеры, решения
Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.
Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.
Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.
Алгоритм
Приведем несколько примеров таких неравенств:
Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:
Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.
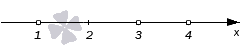
При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.
Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.
Научные основы метода промежутков
Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.
Нахождение нулей числителя и знаменателя
Алгоритм нахождения нулей прост: приравниваем выражения из числителя и знаменателя к нулю и решаем полученные уравнения. При возникновении затруднений можно обратиться к теме «Решение уравнений методом разложения на множители». В этом разделе мы ограничимся лишь рассмотрением примера.
0 в данном случае является одновременно и нулем числителя, и нулем знаменателя.
В общем случае, когда в левой части неравенства дробь, которая не обязательно является рациональной, числитель и знаменатель точно также приравниваются к нулю для получения уравнений. Решение уравнений позволяет найти нули числителя и знаменателя.
Определение знаков на интервалах
Определить знак интервала просто. Для этого можно найти значение выражения из левой части неравенства для любой произвольно выбранной точки из данного интервала. Полученный знак значения выражения в произвольно выбранной точке промежутка будет совпадать со знаком всего промежутка.
Рассмотрим это утверждение на примере.
Можно использовать еще один способ определения знаков. Для этого мы можем найти знак на одном из интервалов и сохранить его или изменить при переходе через нуль. Для того, чтобы все сделать правильно, необходимо следовать правилу: при переходе через нуль знаменателя, но не числителя, или числителя, но не знаменателя мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная. Если мы получили точку, которая является одновременно нулем числителя и знаменателя, то поменять знак на противоположный можно только в том случае, если сумма степеней выражений, дающих этот нуль, нечетная.
Если вспомнить неравенство, которое мы рассмотрели в начале первого пункта этого материала, то на крайнем правом промежутке мы можем поставить знак « + ».
Теперь обратимся к примерам.
Нули знаменателя отметим пустыми точками.
Так как мы имеем дело с нестрогим неравенством, то оставшиеся черточки заменяем обычными точками.
Применение метода интервалов особенно эффективно в случаях, когда вычисление значения выражения связано с большим объемом работы. Примером может стать необходимость вычисления значения выражения
Будем считать, что с правилами определения знаков для промежутков мы разобрались. Идем дальше.