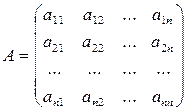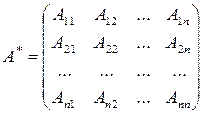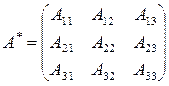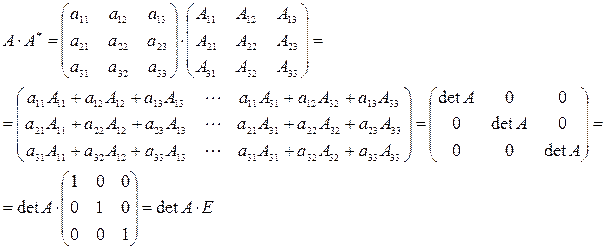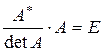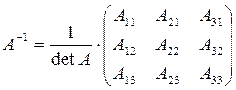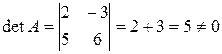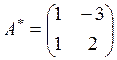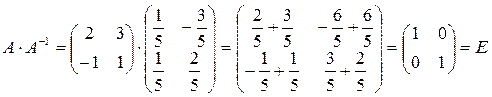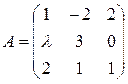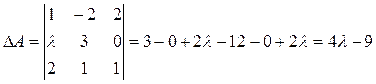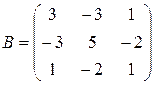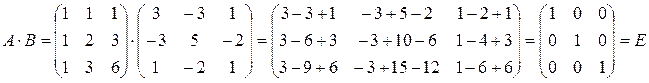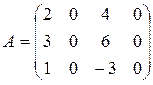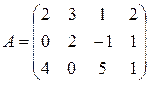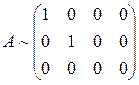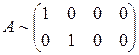Что значит невырожденная матрица
Невырожденная матрица
Невырожденная матрица (иначе Неособенная матрица) ― квадратная матрица, определитель которой отличен от нуля. В противном случае она называется вырожденной.
Для квадратной матрицы 
Полезное
Смотреть что такое «Невырожденная матрица» в других словарях:
невырожденная матрица — неособенная матрица — [http://www.iks media.ru/glossary/index.html?glossid=2400324] невырожденная матрица Квадратная матрица, определитель которой отличен от нуля; ее столбцы линейно независимы (см. Линейная зависимость векторов).… … Справочник технического переводчика
Невырожденная матрица — [non singular matrix] квадратная матрица, определитель которой отличен от нуля; ее столбцы линейно независимы (см. Линейная зависимость векторов). Квадратная матрица обратима тогда и только тогда, когда она невырожденная … Экономико-математический словарь
невырожденная матрица — neypatingoji matrica statusas T sritis fizika atitikmenys: angl. non singular matrix; regular matrix vok. nichtausgeartete Matrix, f; nichtsinguläre Matrix, f; reguläre Matrix, f rus. невырожденная матрица, f; неособенная матрица, f pranc.… … Fizikos terminų žodynas
НЕВЫРОЖДЕННАЯ МАТРИЦА — неособенная матриц а, квадратная матрица, определитель к рой отличен от нуля. Для квадратной матрицы Анад полем невырожденность эквивалентна каждому из следующих условий: 1)A обратима; 2) строки (столбцы) матрицы Алинейно независимы; 3)… … Математическая энциклопедия
МАТРИЦА — прямоугольная таблица состоящая из т строк и n столбцов; её паз. M. размера Элементами(первый индекс указывает номер строки, второй номер столбца) M. могут быть числа, ф ции пли др. величины, над к рыми можно производить алгебраич. операции. M.… … Физическая энциклопедия
Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия
Матрица линейного оператора — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Обратная матрица — Обратная матрица такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для… … Википедия
ЖОРДАНОВА МАТРИЦА — квадратная блочно диагональная матрица J над полем к, имеющая вид где Jm(l) квадратная матрица порядка твида Матрица J т(l)называется жордановой клеткой порядка m с собственным числом к. Каждая клетка определяется элементарным делителем (см. [5]) … Математическая энциклопедия
Вырожденная матрица — Вырожденной или сингулярной называют квадратную матрицу, определитель которой равен нулю. Эквивалентные условия вырожденности Используя различные понятия линейной алгебры, можно привести различные условия вырожденности: Строки или столбцы матрицы … Википедия
Невырожденная матрица
Невырожденная матрица [non-singular matrix] — квадратная матрица, определитель которой отличен от нуля; ее столбцы линейно независимы (см. Линейная зависимость векторов). Квадратная матрица обратима тогда и только тогда, когда она невырожденная.
Смотреть что такое «Невырожденная матрица» в других словарях:
невырожденная матрица — неособенная матрица — [http://www.iks media.ru/glossary/index.html?glossid=2400324] невырожденная матрица Квадратная матрица, определитель которой отличен от нуля; ее столбцы линейно независимы (см. Линейная зависимость векторов).… … Справочник технического переводчика
Невырожденная матрица — (иначе Неособенная матрица) ― квадратная матрица, определитель которой отличен от нуля. В противном случае она называется вырожденной. Для квадратной матрицы над полем невырожденность эквивалентна каждому из следующих условий: обратима, то есть… … Википедия
невырожденная матрица — neypatingoji matrica statusas T sritis fizika atitikmenys: angl. non singular matrix; regular matrix vok. nichtausgeartete Matrix, f; nichtsinguläre Matrix, f; reguläre Matrix, f rus. невырожденная матрица, f; неособенная матрица, f pranc.… … Fizikos terminų žodynas
НЕВЫРОЖДЕННАЯ МАТРИЦА — неособенная матриц а, квадратная матрица, определитель к рой отличен от нуля. Для квадратной матрицы Анад полем невырожденность эквивалентна каждому из следующих условий: 1)A обратима; 2) строки (столбцы) матрицы Алинейно независимы; 3)… … Математическая энциклопедия
МАТРИЦА — прямоугольная таблица состоящая из т строк и n столбцов; её паз. M. размера Элементами(первый индекс указывает номер строки, второй номер столбца) M. могут быть числа, ф ции пли др. величины, над к рыми можно производить алгебраич. операции. M.… … Физическая энциклопедия
Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия
Матрица линейного оператора — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Обратная матрица — Обратная матрица такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для… … Википедия
ЖОРДАНОВА МАТРИЦА — квадратная блочно диагональная матрица J над полем к, имеющая вид где Jm(l) квадратная матрица порядка твида Матрица J т(l)называется жордановой клеткой порядка m с собственным числом к. Каждая клетка определяется элементарным делителем (см. [5]) … Математическая энциклопедия
Вырожденная матрица — Вырожденной или сингулярной называют квадратную матрицу, определитель которой равен нулю. Эквивалентные условия вырожденности Используя различные понятия линейной алгебры, можно привести различные условия вырожденности: Строки или столбцы матрицы … Википедия
Алгебра матриц
Автор: Lida Lysenko, 10 Сентября 2010 в 22:54, курсовая работа
Описание работы
При решении различных задач математики очень часто приходится иметь дело с таблицами чисел, называемых матрицами. С помощью матриц удобно решать системы линейных уравнений, выполнять многие операции с векторами, решать различные задачи компьютерной графики и другие инженерные задачи. Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество п столбцов. Числа т и п называются порядками матрицы. В случае, если т = п, матрица называется квадратной, а число m = n — ее порядком.
Содержание
Глава I. Алгебра матриц……………………………………………………………. 3
1. Понятие матрицы…………………………………………………………..3
2. Виды матриц………………………………………………………………..3
3. Основные операции над матрицами и их свойства……………………. 5
3.1. Сложение матриц……………………………………………………. 5
3.2. Умножение матрицы на число………………………………………. 5
3.3. Произведение матриц………………………………………………….6
4. Вырожденные и невырожденные матрицы………………………………8
5. Обратная матрица…………………………………………………………..8
6. Понятие и основные свойства определителя…………………………….10
7. Транспонирование…………………………………………………………11
Глава II. Реализация матричных операций в Mathcad……………………………..12
Заключение…………………………………………………………………………. 17
Литература…………………………………………………………………………….18
Работа содержит 1 файл
Алгебра матриц.doc
Среди всех диагональных матриц (1.5) с совпадающими элементами d1 = d2 = … = dn = = d особо важную роль играют две матрицы. Первая из этих матриц получается при d = 1, называется единичной матрицей n-го порядка и обозначается символом Е. Вторая матрица получается при d = 0, называется нулевой матрицей n-го порядка и обозначается символом O. Таким образом,
В силу доказанного выше А Е = Е А и А О = О А. Более того, легко показать, что
А Е = Е А = А, А О = О А = 0. (1.6)
Первая из формул (1.6) характеризует особую роль единичной матрицы Е, аналогичную той роли, которую играет число 1 при перемножении вещественных чисел. Что же касается особой роли нулевой матрицы О, то ее выявляет не только вторая из формул (1.6), но и элементарно проверяемое равенство
В заключение заметим, что понятие нулевой матрицы можно вводить и для неквадратных матриц (нулевой называют любую матрицу, все элементы которой равны нулю).
4. Вырожденные и невырожденные матрицы
Матрица называется вырожденной, если ее определитель равен нулю, и невырожденной, если определитель матрицы отличен от нуля.
, = 12-12 = 0; А – вырожденная матрица.
Теорема. Произведение матриц есть вырожденная матрица тогда и только тогда, когда хотя бы один из множителей есть вырожденная матрица.
Необходимость. Пусть АВ – вырожденная матрица, т.е. =0. Тогда, в силу того, что определитель произведения матриц равен произведению определителей перемножаемых матриц, имеем Это значит, что хотя бы одна из матриц А или В является вырожденной.
Замечание. Доказанная теорема справедлива для любого числа множителей.
5. Обратная матрица
Квадратная матрица В называется обратной по отношению к матрице А такого же размера, если
В – матрица обратная к А.
Теорема. Если для данной матрицы обратная существует, то она определяется однозначно.
Предположим, что для матрицы А существуют матрицы Х и У, такие, что
Умножая одно из равенств, например, АХ = Е слева на У, получим У(АХ) = УЕ. В силу ассоциативности умножения имеем (УА)Х = УЕ. Поскольку УА = Е, то ЕХ = УЕ, т.е. Х = У. Теорема доказана.
Теорема (необходимое и достаточное условие существования обратной матрицы).
Достаточность. Пусть дана невырожденная матрица порядка n
так что ее определитель 0. Рассмотри матрицу, составленную из алгебраических дополнений к элементам матрицы А:
ее называют присоединенной к матрице А.
Найдем произведения матриц АА * и А * А. Обозначим АА * через С, тогда по определению произведения матриц имеем: Сij = аi1А 1j + а i2А 2j + … + а inАnj;
Аналогично доказывается, что произведение А на А * равно той же матрице С. Таким образом, имеем А * А = АА * = С. Отсюда следует, что
6. Понятие и основные свойства определителя
Рассмотрим произвольную квадратную матрицу любого порядка п:
С каждой такой матрицей свяжем вполне определенную численную характеристику, называемую определителем, соответствующим этой матрице.
Если порядок n матрицы (1.7) равен единице, то эта матрица состоит из одного элемента аi j определителем первого порядка соответствующим такой матрице, мы назовем величину этого элемента.
Если далее порядок п матрицы (1.7) равен двум, т. е. если эта матрица имеет вид
то определителем второго порядка, соответствующим такой матрице, назовем число, равное а11 а22 — а12 а21 и обозначаемое одним из символов:
Итак, по определению
Формула (1.9) представляет собой правило составления определителя второго порядка по элементам соответствующей ему матрицы. Словесная формулировка этого правила такова: определитель второго порядка, соответствующий матрице (1.8), равен разности произведения элементов, стоящих на главной диагонали этой матрицы, и произведения элементов, стоящих на побочной ее диагонали. Определители второго и более высоких порядков находят широкое применение при решении систем линейных уравнений.
Транспонированная матрица — матрица AT, полученная из исходной матрицы A заменой строк на столбцы.
Если А = Ат, матрица симметрична.
II. Реализация матричных операций в Mathcad
Рассмотрим, как выполняются операции с матрицами в системе MathCad. Простейшие операции матричной алгебры реализованы в MathCad в виде операторов. Написание операторов по смыслу максимально приближено к их математическому действию. Каждый оператор выражается соответствующим символом. Рассмотрим матричные и векторные операции MathCad 2001. Векторы являются частным случаем матриц размерности n x 1, поэтому для них справедливы все те операции, что и для матриц, если ограничения особо не оговорены (например, некоторые операции применимы только к квадратным матрицам n x n). Какие-то действия допустимы только для векторов (например, скалярное произведение), а какие-то, несмотря на одинаковое написание, по-разному действуют на векторы и матрицы.
При работе с матрицами используется панель инструментов “Матрицы”
Рис.1 Панель инструментов Матрицы
Для того, чтобы выполнить какую-либо операцию с помощью панели инструментов, нужно:
Это означает, например, что вычислить определитель матрицы можно, выполнив команду Символы/Матрицы/ Определитель.
Номер первой строки (и первого столбца) матрицы MathCAD хранит в переменной ORIGIN. По умолчанию отсчет ведется от нуля. В математической записи чаще принято вести отсчет от 1. Для того, чтобы MathCAD вел отсчет номеров строк и столбцов от 1, нужно задать значение переменной ORIGIN:=1.
Что значит невырожденная матрица
4.1 ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ

Легко показать, что

Рангом матрицы А (обозначается rang А или r ( A )) является наибольший порядок порожденных ею миноров (определителей), отличных от нуля. Всякий отличный от нуля минор матрицы, порядок которого равен ее рангу, называется ее базисным минором. Строки и столбцы, участвующие в образовании базисного минора, также будут базисными. Матрица может иметь несколько базисных миноров, однако все их порядки одинаковы и равны рангу матрицы.
Ранг матрицы не изменится, если:
1) строки и столбцы матрицы поменять местами;
2) переставить местами два любых ее столбца (строки);
3) удалить из нее столбец (строку), все элементы которого равны нулю;
4) удалить из нее столбец (строку), являющийся линейной комбинацией остальных ее столбцов (строк);
5) умножить ее произвольный столбец (строку) на любое отличное от нуля число;
6) к любому ее столбцу (строке) прибавить произвольную линейную комбинацию остальных столбцов (строк) этой матрицы.
Преобразования 2) ‑ 6) называются элементарными. Две матрицы являются эквивалентными, если одна получается из другой с помощью элементарных преобразований и обозначается как А
Для рангов матриц справедливы следующие соотношения:
1) r (A + В ) 
3) r (A В ) 
5) r ( A В ) = r ( A ), если В – квадратная матрица и D ( В ) 
ЧАСТЬ 2. НЕВЫРОЖДЕННЫЕ МАТРИЦЫ
Дата добавления: 2015-08-14 ; просмотров: 6077 ; Нарушение авторских прав
3.1. Основные понятия
Пусть А — квадратная матрица n-го порядка
Квадратная матрица А называется невырожденной, если определитель Δ = det А не равен нулю: Δ = det А ≠ 0. В противном случае (Δ = 0) матрица А называется вырожденной.
Матрицей, союзной к матрице А, называется матрица
где Aij — алгебраическое дополнение элемента аij данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).
3.2. Обратная матрица
Теорема 3.1.Всякая невырожденная матрица имеет обратную.
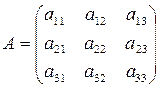
Составим союзную матрицу
и найдем произведение матриц А и А *
Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2). Аналогично убеждаемся, что
Равенства (3.2) и (3.3) перепишем в виде
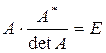
Сравнивая полученные результаты с определением (3.1), получаем
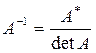
Отметим свойства обратной матрицы:
1. 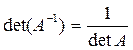
Решение: 1) Находим det A:
Решение: Всякая невырожденная матрица имеет обратную. Найдем определитель матрицы А:
Пример 3.3. Показать, что матрица А является обратной для В, если
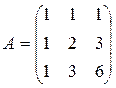
Решение: Найдем произведение матриц А и В:
Аналогично В · А = Е. Следовательно, матрица А является обратной для В.
Рассмотрим матрицу А размера, т х п.
Выделим в ней k строк и k столбцов (k ≤ min(m;n)). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы. В матрице А пунктиром выделен минор 2-го порядка. (Заметим, что таких миноров можно составить 
Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается r, r(А) или rang A.
Очевидно, что 0 ≤ г ≤ min(m; n), где min(m; n) — меньшее из чисел m и п.
Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.
Пример 3.4. Найти ранг матрицы:
Решение: Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля 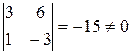
Отметим свойства ранга матрицы:
1. При транспонировании матрицы ее ранг не меняется.
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.
3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы (см. с. 12).
Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.
Пример 3.5. Найти ранг матрицы используя результаты примера 1.4.
Решение: В примере 1.4 показано, что
Таким образом, ранг матрицы А равен r(А) = 2.