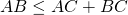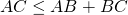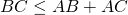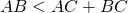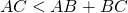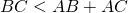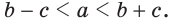Что значит неравенство треугольников
Неравенство треугольника
Нера́венство треуго́льника в геометрии, функциональном анализе и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Неравенство треугольника включается как аксиома в определение метрического пространства, нормы и т.д.; также, часто является теоремой в различных теориях.
Содержание
Евклидова геометрия
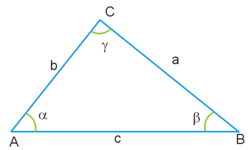
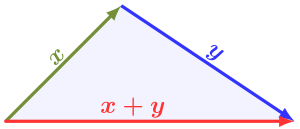
Пусть дан треугольник 
Тогда 
причём равенство 
достигается только тогда, когда треугольник вырожден, и точка 
лежит строго между 
и 
.
Евклид в Началах доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного. Из неё выводится теорема о том, что против большей стороны треугольника лежит больший внутренний угол. Далее, методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. А из этой теоремы выводится неравенство треугольника.
Нормированное пространство
Пусть 
— нормированное векторное пространство, где 
— произвольное множество, а 
— определённая на норма. Тогда по определению последней справедливо:
Гильбертово пространство
Метрическое пространство
Пусть 
— метрическое пространство, где — произвольное множество, а 
— определённая на метрика. Тогда по определению последней
Вариации и обобщения
Обратное неравенство треугольника
Следствием неравенства треугольника в нормированном и метрическом пространствах являются следующие неравенства:
Неравенство треугольника для трёхгранного угла
Каждый плоский угол выпуклого трёхгранного угла меньше суммы двух других его плоских углов.
Полезное
Смотреть что такое «Неравенство треугольника» в других словарях:
Обратное неравенство треугольника — Неравенство треугольника в геометрии, функциональном анализе и смежных дисциплинах это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон.… … Википедия
Неравенство Птолемея — Неравенство Птолемея: Для любых точек плоскости выполнено неравенство причем равенство достигается тогда и только тогда, когда (выпуклый) вписанный четырехугольник или точки ABCD лежат на одной прямой. Содержание … Википедия
Неравенство Минковского — это неравенство треугольника для пространств функций с интегрируемой ой степенью. Содержание 1 Формулировка 2 Доказательство … Википедия
Неравенство Эрдёша — Неравенство Эрдёша Морделла (неравенство Эрдёша Морделла Барроу) устанавливает связь между расстояниями от точки внутри треугольника до его сторон с расстояниями от той же точки до вершин треугольника. Пусть точка лежит внутри… … Википедия
Неравенство Эрдёша — Морделла — Неравенство Эрдёша Морделла (неравенство Эрдёша Морделла Барроу) Пусть точка O лежит внутри треугольника ABC. Обозначим расстояния от точки O до сторон BC,CA,AB треугольника через da,db,dc, а расстояния от точки O до вершин… … Википедия
Неравенство Эрдеша — Морделла — Неравенство Эрдёша Морделла (неравенство Эрдёша Морделла Барроу) Пусть точка O лежит внутри треугольника ABC. Обозначим расстояния от точки O до сторон BC,CA,AB треугольника через da,db,dc, а расстояния от точки O до вершин A,B,C через… … Википедия
Неравенство Коши — Буняковского — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши … … Википедия
Неравенство Коши — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы. Неравенство Коши Буняковского иногда, особенно в иностранной… … Википедия
с равенством только в вырожденном случае треугольника нулевой площади. В евклидовой геометрии и некоторых других геометриях неравенство треугольника является теоремой о расстояниях, и оно записывается с использованием векторов и векторных длин ( норм ):
СОДЕРЖАНИЕ
Евклидова геометрия
Математическое выражение ограничения на сторонах треугольника
Более сжатая форма этой системы неравенств может быть представлена следующим образом:
В терминах любого выражения площади неравенство треугольника, наложенное со всех сторон, эквивалентно условию, что выражение под знаком квадратного корня является действительным и больше нуля (так что выражение площади является действительным и больше нуля).
Прямоугольный треугольник
В случае прямоугольных треугольников неравенство треугольника специализируется на утверждении, что гипотенуза больше любой из двух сторон и меньше их суммы.
Точно так же в равнобедренном треугольнике ABC углы удовлетворяют следующим условиям:
Эта теорема, устанавливающая неравенства, уточняется теоремой Пифагора до того, что квадрат длины гипотенузы равен сумме квадратов двух других сторон.
Примеры использования
Для удовлетворения всех этих неравенств требуется
Обобщение на любой многоугольник
Неравенство треугольника может быть расширено математической индукцией на произвольные многоугольные пути, показывая, что общая длина такого пути не меньше, чем длина прямой линии между его конечными точками. Следовательно, длина любой стороны многоугольника всегда меньше суммы длин сторон других многоугольников.
Пример обобщенного неравенства многоугольника для четырехугольника
Эти неравенства при a > 0 сводятся к следующему
Отношения с кратчайшими путями
Это обобщение можно использовать, чтобы доказать, что кратчайшая кривая между двумя точками в евклидовой геометрии является прямой линией.
Converse
Верно и обратное утверждение теоремы о неравенстве треугольника: если три действительных числа таковы, что каждое меньше суммы других, то существует треугольник с этими числами в качестве длин сторон и с положительной площадью; и если одно число равно сумме двух других, существует вырожденный треугольник (то есть с нулевой площадью) с этими числами в качестве длин сторон.
Чтобы действительное число h удовлетворяло этому требованию, оно должно быть неотрицательным: час 2 <\ displaystyle h ^ <2>> 
Обобщение на более высокие измерения
Нормированное векторное пространство
В нормированном векторном пространстве V одним из определяющих свойств нормы является неравенство треугольника:
Примеры норм
Неравенство треугольника полезно в математическом анализе для определения наилучшей верхней оценки размера суммы двух чисел с точки зрения размеров отдельных чисел.
Существует также нижняя оценка, которую можно найти с помощью неравенства обратного треугольника, которое гласит, что для любых действительных чисел x и y :
Метрическое пространство
В метрическом пространстве M с метрикой d неравенство треугольника является требованием для расстояния :
Обратное неравенство треугольника
В случае нормированного векторного пространства утверждение таково:
Объединение этих двух утверждений дает:
Обращение в пространстве Минковского
Неравенство треугольника
Неравенство треугольника описывает зависимость между длинами сторон любого треугольника.
Теорема (неравенство треугольника):
Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.
Для трех точек A, B и C это означает, что
Равенство в этих соотношениях может быть только в том случае, когда все три точки лежат на одной прямой.
Отсюда следует, что длина любой стороны треугольника меньше суммы длин двух других сторон.
Например, неравенство треугольника для треугольника ABC записывается так
Как неравенство треугольника используется в решении задач, мы рассмотрим позже.
Содержание:
Неравенство треугольника:
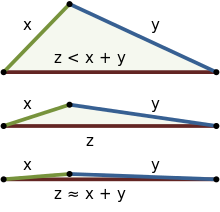
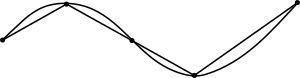
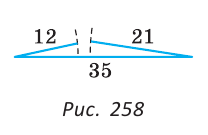
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС 12+21 (рис. 258).
Замечание. Из неравенств треугольника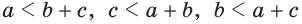 
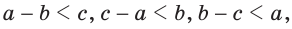
следует, что 
то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо 
Пример:
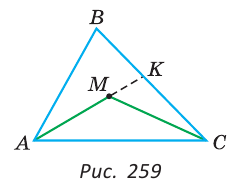
Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.
Решение:
Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС 
B (рис. 108, а).
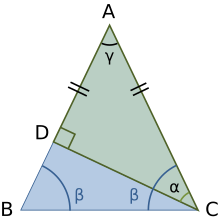
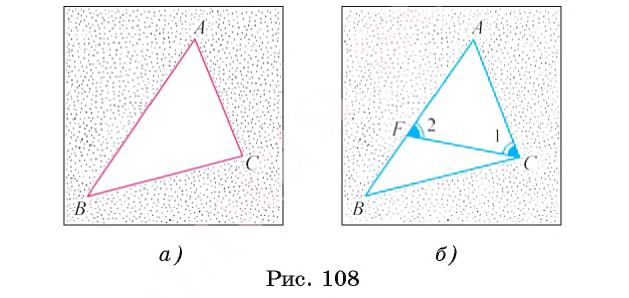
2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).
3) Так как АF 1.
4) Угол 2 является внешним углом треугольника ВFС, следовательно, 2 > B.
5) Так как треугольник FАС является равнобедренным, то 1 = 2.
Таким образом, BСА > 1, 1 = 2 и 2 > B.
Отсюда получаем, что ВСА > B.
Теорема 2. В треугольнике против большего угла лежит большая сторона.
1) Пусть в треугольнике АBС С > B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.
2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ C.
В каждом из этих случаев получаем противоречие с условием: C > B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.
Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.
Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.
Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.
Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.
Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.
Неравенство треугольника
Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.
Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.
1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ l, следовательно, верно неравенство АВF > 2.
4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Неравенство треугольника
Всего получено оценок: 337.
Всего получено оценок: 337.
Любая фигура имеет некие рамки, пропорции длин сторон. В реальной жизни они помогают определить, можно ли изготовить треугольное основание определенных пропорций, насколько возможно создать линзу той или иной формы или может ли удержаться табуретка на треугольном, квадратном или любом другом основании. В теоретической геометрии пропорции, как правило, применяют для решения задач на доказательство или для определения правильности условия задачи.
Теорема о неравенстве треугольника
Именно с этой теоремы должно начинаться любое решение задачи. Но, как правило, это действие опускают. Считается, что составитель задач не может предложить условие с несуществующим треугольником.
Теорема о неравенстве сторон треугольника гласит, что каждая сторона треугольника всегда меньше или равна сумме двух других его сторон.
Доказать это определение можно двумя способами: через аксиому Евклида или через высоту треугольника. Последний способ более логичен, тогда как второй – короче. Какой выбрать – решает доказывающий.
Доказательство через аксиому
Существует аксиома, которая говорит, что для трех точек А, В, С не лежащих на одной прямой справедливо утверждение: АВ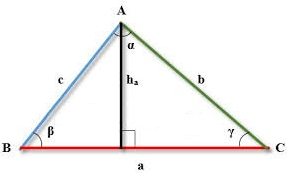 
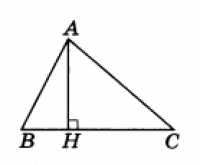
Рис. 2. Рисунок к доказательству
В произвольном треугольнике АВС проведем высоту АН. Высота разобьет произвольный треугольник на два прямоугольных. Тогда для каждого из прямоугольных треугольников в виде неравенств запишем, что катет всегда меньше гипотенузы.
ВН 
Рис. 3. Рисунок к доказательству